Стационарные и нестационарные модели
Стационарныминазывают объекты и процессы, параметры которых не изменяются с течением времени. Зачастую стационарность модели является следствием намеренного упрощения описываемого объекта или процесса. Примером стационарной модели может служить дифференциальное уравнение с постоянными, т.е. не зависящими от времени коэффициентами:
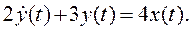
Большинство реальных систем и процессов не обладает свойством стационарности: со временем изнашиваются соприкасающиеся детали механизмов, в доменной печи обгорают свод и стены топки, изменяя теплоотдачу, сечение водопроводных труб уменьшается за счет отложения на стенках карбонатов. Под воздействием внешней среды со временем в результате так называемых причин естественного старения изменяются такие характеристики материалов, как упругость, прозрачность, магнитная и диэлектрическая проницаемость, теплопроводность и др. Такие изменения, разумеется, нежелательны. Но иногда изменения свойств с течением времени бывают нужны: например, в термисторах используется свойство изменения внутреннего электрического сопротивления в зависимости от температуры внешней среды (поскольку температура изменяется во времени, то и сопротивление в конечном счете зависит от времени). Если изменения параметров незначительны за время рассмотрения процесса или системы, то пользуются приближенными стационарными моделями, которые можно исследовать аналитически, благодаря хорошо разработанному математическому аппарату.
Для нестационарной моделиважно, что изменения параметров происходят не за любое время вообще, а за время, сопоставимое со временем, в течение которого процесс исследуется, например, за время переходного процесса. Пример нестационарной модели – уравнение с коэффициентами, явно зависящими от времени:
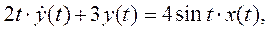
в котором даже одного из коэффициентов 2t или 4sin(t) вполне достаточно, чтобы модель была нестационарной.
Нестационарные модели являются существенно более сложными, чем стационарные. Аналитическое решение для них возможно получить только в отдельных, довольно редких случаях. В общем случае исследовать нестационарные модели удается только с помощью численных методов.
Дата добавления: 2016-02-02; просмотров: 793;
