Детерминированные и вероятностные модели
Детерминированныминазываются модели, в которых отсутствуют какие бы то ни было случайные изменения: внешних воздействий, внутренних параметров и самих переменных. В таких моделях все поведение объекта определяется конкретными значениями начальных условий и входных переменных. Иначе говоря, в них все точно определено (детерминировано).
Вероятностнымиявляются модели, в которых учитывается случайный характер изменений значений входных, промежуточных и выходных переменных, а также параметров моделируемого объекта. В том случае, когда независимой переменной служит время, случайные процессы, а также и соответствующие вероятностные модели, их описывающие, называются стохастическими. Такие модели характеризуются функциями или плотностями распределения вероятностей и средними характеристиками смещения и рассеяния, например, математическим ожиданием и дисперсией.
Существуют различные точки зрения на реальный характер процессов, протекающих в нашем мире. Одна из них заключается в том, что абсолютно все процессы случайны, но среди них есть более случайные, с большим разбросом значений реализаций относительно средних характеристик, и менее случайные, со значениями, близкими к средним. Полярная точка зрения состоит в том, что наш мир детерминирован, а случайность характеризует степень нашей неосведомленности об истинном положении дел. По мере познания случайность должна отступать, уступая место детерминированному описанию. С нашей точки зрения истина, как всегда, находится где-то посередине, но в любом случае и детерминированные, и случайные модели имеют право на существование, взаимно дополняя друг друга. К этому вопросу целесообразно вернуться позже, при рассмотрении свойства истинности моделей (п. 1.5).
Можно рассмотреть на примере графиков функций распределения вероятностей (рис. 1.10) постепенный переход от одних вероятностных моделей (1 – равномерное распределение) к другим вероятностным моделям (2 и 3 – нормальное распределение с разными значениями параметра), а также в пределе и к детерминированной модели 4.
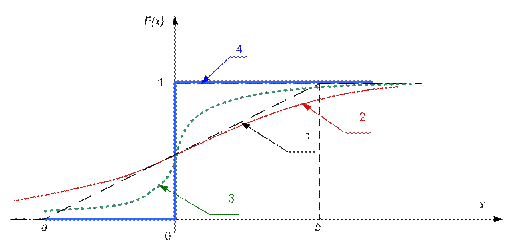
Рис.1.10. Переход от вероятностных моделей: равномерного распределения 1 (на интервале ab) и нормального распределения 2, 3 к детерминированной модели 4
Дата добавления: 2016-02-02; просмотров: 1264;
