Еквівалентність множників нарощування простих та складних відсотків

У відповідності з рівнянням простих відсотків множник наро­щення простих відсотків — це величина (1 + і*n).

А у відповідності з рівнянням складних відсотків множник нарощення складних відсотків — це величина (1 + і)ⁿ.

Позначимо ставку дохідності, яка розрахована за простими процентами як і_is, а ставку розраховану за складними процента­ми, як і_ic.

Тоді, умову еквівалентності простих та складних множників нарощування відсотків можна записати у вигляді наступного рівняння:

(4.1)

З рівняння (4.1) можна виразити еквівалентні прості та склад­ні ставки дохідності.

Проста ставка за відомої склад­ної ставки дохідності розраховується за формулою:

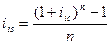(4.2)

Складна ставка за відомої простої ставки дохідності знаходиться за наступною формулою:

(4.3)

Графічна ілюстрація співвідношення множ­ників нарощення наведена на рис.4.1.

Кут нахилу функцій, зображених на рис. 4.1, залежить від величини ставки дохідності і. Чим більша ця ставка, тим швидше зростає вартість у часі, і тим крутіший нахил відпо­відної функції.

(1+і)ⁿ

(1+і*n)

1 і

1 t

Рис. 4.1. Графік множників нарощення вартості за правилами простих та складних відсотків

З рис. 4.1 неважко побачити, що на проміжку t є (0;1) більшими є значення функції множника нарощення простих відсотків, а на проміжку t є (1;n), навпаки — значення функції, що відповідає пра­вилу складних відсотків. Графіки функцій множників нарощення перетинаються лише один раз при t = 1. Тобто, еквівалентність (рів­ність) множників нарощування простих та складних відсотків, за умови однакових параметрів і та п, досягається лише за одно­разового нарощення коштів.

В цілому, порівнюючи множники нарощенняпростих та складних відсотків можна зробити відповідні висновки.

Якщо взяти однакові за величиною, але різні за правилом на­рощення відсотків річніставки, то:

· для строку меншогоза один рік вартість нарощується швидше за правилом простихвідсотків;

· для строку більшого,ніж один рік вартість нарощується швидше за правилом складнихвідсотків;

· для строку 1рік множники нарощення дорівнюють.

Оскільки у комерційних розрахунках тип множників нарощення зазвичай обирають відповідно з принципами максимізації прибутку, то існує правило — у короткострокових фінансових угодах нарощення краще здійснювати за простими відсотками, а у довгострокових — за складними відсотками.