Методика обчислень за правилом простих відсотків
Часто під час здійснення фінансово-економічних операцій нарахування процентів відбувається не один раз, а з певною періодичністю. За цих умов важливо знати методику нарахування відсотків. У межах фінансових розрахунків виділяють дві основні методики — простих процентів і складних процентів, а також їх комбінації.
Правило простих процентів зазвичай застосовують у короткострокових фінансових угодах та у випадках, коли проценти не додають до основної суми боргу, а періодично виплачують. Цей метод не передбачає реінвестування, отже — й капіталізації процентів.
Сутність методу нарахування за простими відсотками полягає в тому, що впродовж усього терміну дії фінансової угоди проценти нарощують лише на початкову суму.
Кінцева сума (FV), тобто майбутня величина, яку одержить інвестор після всіх нарахувань, за правилом простих процентів дорівнює (декурсивний метод):
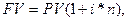 (2.1)
(2.1)
де PV – теперішня вартість грошей;
n (або t)– строк позики;
і (або r)– відсоткова ставка.
Вираз (2.1) є формулою нарощення за простими процентами, а величину (1+і*n) називають множником нарощування простих процентів.
За антисипативним методом нарахування простих відсотків кінцева сума (FV) дорівнює:
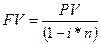 (2.2)
(2.2)
Аналогічним чином у разі нарахування відсотків щоквартально чи щомісячно, розраховується нарощена сума за декурсивним методом, тобто первісна сума множиться на 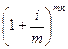 , де m – кількість нарахувань.
, де m – кількість нарахувань.
Приклад 1. Початкова сума боргу складає 3000 грн. Визначити величину нарощеної суми через 4 роки при застосуванні декурсивного і антисипативного методів нарахування відсотків. Річна ставка – 12 %.
Декурсивний метод:
FV = 3000 (1 + 0,12*4) = 4440 грн.
Антисипативний метод:
FV = 3000 / (1 – 0,12*4) = 5769 грн.
При рівності позичкового відсотку та облікової ставки, нарощення початкової суми в другому випадку (антисипативний спосіб) йде швидше, тому декурсивний спосіб більш вигідний для позичальника, а антисипативний – для кредитора. Але це справедливо лише для невеликих відсоткових ставок.
Для коректних обчислень методом простих відсотків величини і та п мають бути взаємоузгоджені (зведені до одних величин часу — років, місяців, днів тощо). Наприклад, коли і — річна ставка доходності, то й величина п має бути в частках року.
Нарощення за правилом простих процентів відбувається за арифметичною прогресією.
За правилом простих відсотків розмір відсотків (величину простого відсотку) обчислюють за формулою:
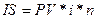 (2.3)
(2.3)
Враховуючи умови прикладу 1, розрахуємо розмір відсотків (декурсивний метод):
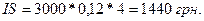
Отже, за незмінної відсоткової ставки, нарощена сума буде зростати відповідно до збільшення строку нарощення.
Виходячи із вищезазначеного, майбутню вартість за правилом простих відсотків можна знайти за формулою:
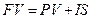 (2.4)
(2.4)
Враховуючи умови попереднього прикладу, знайдемо розмір нарощеної суми:

Отже, розмір простого проценту — це різниця між номінальними величинами кінцевої та початкової вартості:
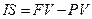 (2.5)
(2.5)
За простими процентами можна виконувати й обернену до нарощування операцію — операцію дисконтування:
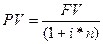 (2.6)
(2.6)
Величину 1/(1+і*n) називають множником дисконтування простих процентів.
Дата добавления: 2016-02-02; просмотров: 1408;
