ОЦЕНКА МСП ПРИ ИЗБЫТОЧНОМ ЧИСЛЕ ОБЪЕКТОВ СРАВНЕНИЯ
Если число сравниваемых объектов 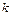 больше n+1, то система уравнений (7.8) будет переопределена. Ее решение следует выполнить методами математической статистики. Выбор метода решения такой переопределенной системы определяется наличием информации о точности значений факторов и цен сравниваемых объектов. В том случае, если точность названных величин достоверно известна и ошибки в значениях факторов цен имеют случайный характер, решение этой системы следует выполнить по методу наименьших квадратов. Для этого ее переписывают так
больше n+1, то система уравнений (7.8) будет переопределена. Ее решение следует выполнить методами математической статистики. Выбор метода решения такой переопределенной системы определяется наличием информации о точности значений факторов и цен сравниваемых объектов. В том случае, если точность названных величин достоверно известна и ошибки в значениях факторов цен имеют случайный характер, решение этой системы следует выполнить по методу наименьших квадратов. Для этого ее переписывают так
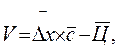 (7.10)
(7.10)
где 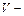 вектор отклонений значений цен сравниваемых объектов, вычисленных по найденному вектору
вектор отклонений значений цен сравниваемых объектов, вычисленных по найденному вектору 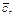 от значений этих цен, полученных из источников ценовой информации.
от значений этих цен, полученных из источников ценовой информации.
Предположим, что значения факторов сравниваемых объектов безошибочны, а точность составляющих вектора 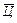 характеризуется матрицей
характеризуется матрицей
 (7.11)
(7.11)
где 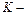 корреляционная матрица вектора
корреляционная матрица вектора 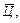
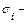 стандарт составляющей вектора
стандарт составляющей вектора 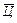 с номером
с номером 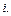 Ошибки составляющих вектора
Ошибки составляющих вектора 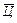 независимы. Поэтому недиагональные элементы в (7.11) равны нулю. Тогда решение по методу наименьших квадратов сведется к минимизации следующего функционала
независимы. Поэтому недиагональные элементы в (7.11) равны нулю. Тогда решение по методу наименьших квадратов сведется к минимизации следующего функционала
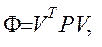 (7.12)
(7.12)
где 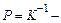 так называемая весовая матрица.
так называемая весовая матрица.
Для достижения минимума (7.12) необходимо взять производную функционала по вектору  и приравнять ее к нулю. То есть записать
и приравнять ее к нулю. То есть записать
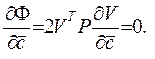 (7.13)
(7.13)
Поскольку на основании (7.10)
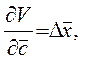
то будет
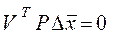 (7.14)
(7.14)
или после трансформирования (7.14)
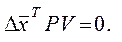 (7.15)
(7.15)
Подставляя (7.10) в (7.15) найдем
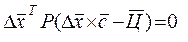
или
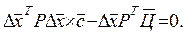 (7.16)
(7.16)
Матрица 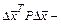 называется матрицей нормальных уравнений. Ее можно обозначить через N.
называется матрицей нормальных уравнений. Ее можно обозначить через N.
Умножая уравнение (7.16) слева на матрицу
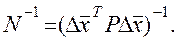
Найдем
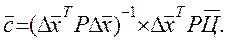 (7.17)
(7.17)
Выражение (7.17) является общим решением задачи при числе сравниваемых объектов, большем n+1.
Зная корреляционную матрицу вектора наблюдений 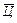 можно вычислить и корреляционную матрицу вектора С.
можно вычислить и корреляционную матрицу вектора С.
При известной зависимости
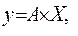 (7.18)
(7.18)
где 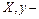 векторы, а
векторы, а 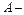 соответствующая матрица, при известной корреляционной матрице
соответствующая матрица, при известной корреляционной матрице 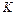 вектора
вектора 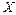 корреляционная матрица вектора
корреляционная матрица вектора 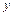 будет
будет
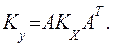 (7.19)
(7.19)
Полагая в (7.17)
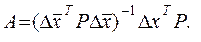 (7.20)
(7.20)
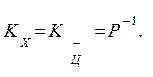 (7.21)
(7.21)
На основе (7.19) получим
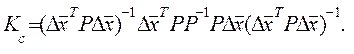 (7.22)
(7.22)
После простых сокращений (7.22) примет вид
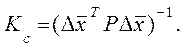 (7.23)
(7.23)
Это есть корреляционная матрица вектора 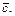 Диагональные члены этой матрицы являются дисперсиями составляющих вектора
Диагональные члены этой матрицы являются дисперсиями составляющих вектора 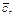 недиагональные – корреляционными моментами этих составляющих.
недиагональные – корреляционными моментами этих составляющих.
При решении в соответствии с (7.17) вместо матрицы 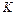 можно сразу задаваться весовой матрицей вектора
можно сразу задаваться весовой матрицей вектора 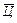 .
.
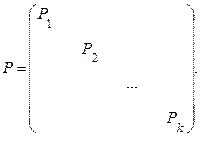 (7.24)
(7.24)
Вес 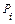 в (7.24) находится так
в (7.24) находится так
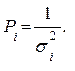 (7.25)
(7.25)
Но этот же вес можно задать из соотношения весов
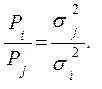 (7.26)
(7.26)
Тогда
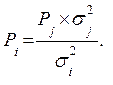 (7.27)
(7.27)
Полагая
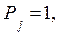
можно записать
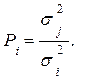 (7.28)
(7.28)
То есть в данном случае какой-либо сопоставляющей вектора 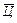 приписывается единичный вес, а веса других вычисляются по (7.28).
приписывается единичный вес, а веса других вычисляются по (7.28).
Решение получается также по (7.17), а матрица
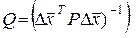
будет не корреляционной, а обратно-весовой. Корреляционная матрица вектора 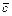 будет
будет
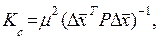 (7.29)
(7.29)
где 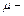 средняя квадратическая ошибка величины, вес которой принят равным единице.
средняя квадратическая ошибка величины, вес которой принят равным единице.
Величина 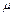 определяется по формуле
определяется по формуле
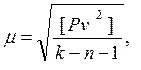 (7.30)
(7.30)
где 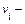 это составляющая с номером i вектора
это составляющая с номером i вектора
 (7.31)
(7.31)
Если обозначить 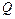 через
через
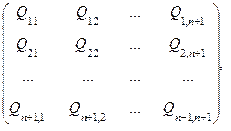 (7.32)
(7.32)
то средняя квадратическая ошибка найденного значения стоимости оцениваемого объекта будет
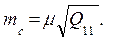 (7.33)
(7.33)
Интервальная оценка стоимости объекта определяется интервалом
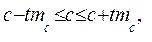 (7.34)
(7.34)
где 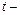 значение статистического параметра распределения Стьюдента, определяемого по доверительной вероятности
значение статистического параметра распределения Стьюдента, определяемого по доверительной вероятности 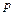 и числу степеней свободы
и числу степеней свободы 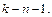
Пример 7.2.Оценить стоимость объекта недвижимости по трем факторам: площади, наличию сада, наличию гаража. Оценку произвести по девяти сравниваемым объектам, приведенным в таблице 7.8.
Таблица 7.8
Таблица сравнения объектов
| Элементы сравнения | Объекты | Оцениваемый | ||||||||
| Площадь | ||||||||||
| Наличие гаража | Есть | Есть | Есть | Нет | Есть | Нет | Есть | Нет | Есть | Есть |
| Наличие сада | Есть | Нет | Есть | Нет | Есть | Нет | Есть | Нет | Нет | Нет |
| Стоимость |
Решение:Таблица коэффициентов системы уравнений (7.10) представлена в табл. 7.9.
Таблица 7.9.
Дата добавления: 2016-02-02; просмотров: 640;
