Способы преобразования сложных структур

Относительная простота расчетов надежности, основанных на использовании параллельно-последовательных структур, делают их самыми распространенными в инженерной практике. Однако не всегда условие работоспособности можно непосредственно представить параллельно-последовательной структурой. В этом случае можно сложную структуру заменить ее эквивалентной параллельно-последовательной структурой. К таким преобразованиям относится:

- преобразование с эквивалентной заменой треугольника на звезду и обратно;

- разложение сложной структуры по базовому элементу.

Существо способа преобразования с помощью эквивалентной замены треугольника на звезду и обратно заключается в том, что узел сложной конфигурации заменяется на узел другой, более простой конфигурации, но при этом подбираются такие характеристики нового узла, что надежности преобразуемой цепи сохранялись прежними.

Пусть, например, требуется заменить треугольник (рис. 4.5.7,а) звездой (рис. 4.5.7,б) при условии, что вероятность отказа элемента a равна q₁₃, элемента b равна q₁₂, элемента c - q₂₃. Переход к соединению звездой не должен изменить надежность цепей 1-2, 1-3, 2-3. Поэтому значение вероятностей отказов элементов звезды q₁, q₂, q₃ должны удовлетворять следующим равенствам:
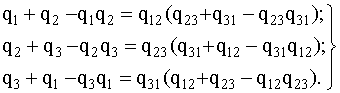(4.5.14)

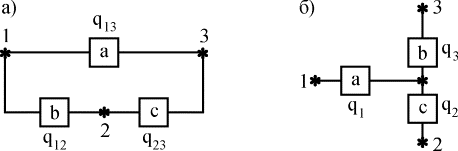
Рис. 4.5.7. Преобразование "треугольник - звезда"

Если пренебречь произведениями вида q_iq_j; q_iq_jq_k, то в результате решения системы уравнения (4.5.14) можно записать:

q₁=q₁₂q₃₁; q₂=q₂₃q₁₂; q₃=q₃₁q₂₃. (4.5.15)

Для обратного преобразования звезды в треугольник

q₁₂= 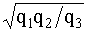; q₂₃= 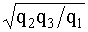; q₃₁= 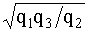. (4.5.16)

Пример 4.5.7. Определить вероятность безотказной работы устройства, структурная схема которого изображена на рис. 4.5.3,б, если известно, что вероятности безотказной работы каждого из элементов схемы равны 0,9, а вероятности отказов равны 0,1.

Решение.

1. Преобразуем соединение элементов 1,2,5 в треугольник (рис. 4.5.8,а), в звезду (рис. 4.5.8, б).

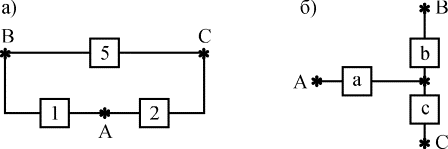
Рис. 4.5.8. К примеру преобразования структуры

2. Определим эквивалентные значения вероятности отказов для новых элементов a, b, c

q_a=q₁q₂=0,1´0,1 = 0,01;

q_b=q₁q₅=0,1´0,1 = 0,01;

q_с=q₂q₅=0,1´0,1 = 0,01.

3. Определим значения вероятности безотказного состояния элементов эквивалентной схемы (рис. 4.5.8,б)

p_a = p_b = p_c = 0,99.

4. Определим вероятность безотказной работы эквивалентного устройства (рис. 4.5.9):

Р = р_a(р_bр₃ + р_cр₄ - р_bр₃р_cр₄) =

= 0,99(0,99´0,9+0,99´0,9 - 0,99´0,9´0,99´0,9) = 0,978.

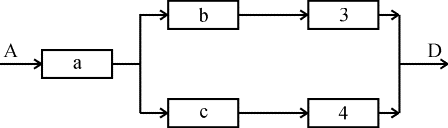
Рис. 4.5.9. Преобразованная структура

Способ преобразования с помощью разложения сложной структуры по некоторому базовому элементу основан на использовании теоремы о сумме вероятностей несовместных событий. В сложной структуре выбирают базовый элемент (или группу базовых элементов) и делаются следующие допущения:

- базовый элемент находится в работоспособном состоянии;

- базовый элемент находится в отказавшем состоянии.

Для этих случаев, представляющих собой два несовместных события, исходная структура преобразовывается в две новые схемы. В первой из них вместо базового элемента ставится "короткое замыкание" цепи, а во второй - разрыв. Вероятности безотказной работы каждой из полученных простых структур вычисляются и умножаются: первая - на вероятность безотказного состояния базового элемента, вторая - на вероятность отказа базового элемента. Полученные произведения складываются. Сумма равна искомой вероятности безотказной работы сложной структуры.

Пример 4.5.8. Решить предыдущий пример методом разложения сложной структуры.

Решение.

1. В качестве базового элемента примем элемент 5 (рис. 4.5.3,б).

2. Закоротим базовый элемент, т.е. сделаем допущение об абсолютной его проводимости. Присоединим к полученной структуре последовательно базовый элемент с характеристикой его надежности р₅. В результате вместо исходной структуры получим новую структуру (рис. 4.5.10,а).

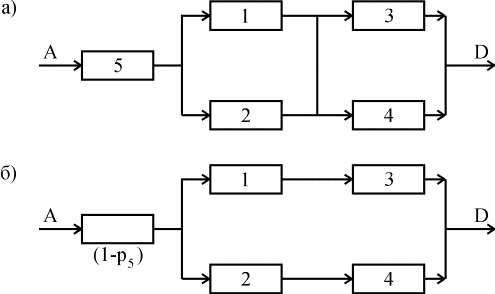
Рис. 4.5.10. Пример разложения мостиковой структуры по базовому элементу

3. Произведем обрыв базового элемента, т.е. сделаем предположение об его абсолютной ненадежности (непроводимости). К полученной структуре присоединим последовательно базовый элемент с характеристикой его ненадежности (1-р₅). В результате получим структуру (рис. 4.5.10,б).

4. Искомая вероятность равна сумме вероятностей структур (рис. 4.5.10,а,б), каждая из которых параллельно-последовательная. Поэтому

Р = р₅[(р₁+р₂-р₁р₂)(р₃+р₄-р₃р₄)] + (1-р₅)[р₁р₃+р₂р₄-р₁р₃р₂р₄]=

= 0,9[(0,9+0,9 - 0,9´0,9) ´ (0,9+0,9 - 0,9´0,9)] +

+ (1-0,9) ´ [0,9´0,9 + 0,9´0,9 - 0,9´0,9´0,9´0,9]»0,978.

Вероятность безотказной работы мостиковой схемы, состоящей из пяти неодинаковых и независимых элементов, можно определить по формуле:

Р=2р₁р₂р₃р₄р₅-р₂р₃р₄р₅-р₁р₃р₄р₅-р₁р₂р₄р₅-р₁р₂р₃р₅-

-р₁р₂р₃р₄+р₁р₃р₅+р₂р₃р₄+р₁р₄+р₂р₅. (4.5.17)

В случае идентичных элементов эта формула принимает вид

Р = 2р⁵-5р⁴+2р³+2р². (4.5.18)

Подставляя соотношение (4.5.18) в формулу (4.5.4), получаем, что в случае использования элементов с постоянной интенсивностью отказов (экспоненциальном законе распределения отказов)

Р(t) = 2ехр(-5λt)-5ехр(-4λt)+2ехр(-3λt)+2ехр(-2λt). (4.5.19)

Среднее время безотказной работы системы Т₀ находим, путем интегрирования уравнения (5.19) в интервале [0,¥]:

Т₀ = 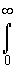2ехр(-5λt)-5ехр(-4λt)+2ехр(-3λt)+2ехр(-2λt)dt=

= (49/60)´(1/λ). (4.5.20)

Пример 4.5.9. Определить вероятность безотказной работы устройства, структурная схема которого изображена на рис. 4.5.3,б, если известно, что вероятности безотказной работы каждого из элементов схемы равны 0,9.

Решение.

Так как все элементы идентичны, воспользуемся формулой (4.5.18); с ее помощью получаем:

Р = 2´0,9⁵ - 5´0,9⁴+2´0,9³ + 2´0,9²»0,978.

Пример 4.5.10. Требуется определить вероятность безотказной работы и среднюю наработку на отказ системы, состоящей из пяти независимых и одинаковых элементов, соединенных по мостиковой схеме (рис. 4.5.3,б); считается, что λ=0,0005ч^-1, t=100ч и все элементы начинают работать в момент времени t=0.

Решение.

1. С помощью формулы (4.5.19) получаем

2. Р₍₁₀₀₎ = 2е^-0,25-5е^-0,2+2е^-0,15+2е^-0,1 = 0,9999.

3. 2. Подставляя полученное значение вероятности безотказной работы в формулу (4.5.20), находим среднюю наработку на отказ

4. Т₀ = 49/(60´0,0005) = 1633,4 ч.