Система с параллельным соединением элементов

На рис. 4.5.6 представлено параллельное соединение элементов 1, 2, 3. Это означает, что устройство, состоящее из этих элементов, переходит в состояние отказа после отказа всех элементов при условии, что все элементы системы находятся под нагрузкой, а отказы элементов статистически независимы.

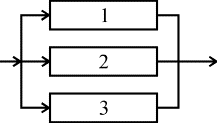
Рис. 4.5.6. Блок-схема системы с параллельным соединением элементов

Условие работоспособности устройства можно сформулировать следующим образом: устройство работоспособно, если работоспособен элемент 1 или элемент 2, или элемент 3, или элементы 1 и 2, 1; и 3, 2; и 3, 1; и 2; и 3.

Вероятность безотказного состояния устройства, состоящего из n параллельно соединенных элементов определяется по теореме сложения вероятностей совместных случайных событий как

Р=(р₁+р₂+...р_n)-(р₁р₂+р₁р₃+...)-(р₁р₂р₃+р₁р₂р_n+...)-... ± (р₁р₂р₃...р_n). (4.5.7)

Для приведенной блок-схемы (рис. 4.5.6), состоящей из трех элементов, выражение (4.5.7) можно записать:

Р=р₁+р₂+р₃-(р₁р₂+р₁р₃+р₂р₃)+р₁р₂р₃.

Применительно к проблемам надежности, по правилу умножения вероятностей независимых (в совокупности) событий, надежность устройства из n элементов вычисляется по формуле

Р = 1- , (4.5.8)

т.е. при параллельном соединении независимых (в смысле надежности) элементов их ненадежности (1-p_i=q_i) перемножаются.

В частном случае, когда надежности всех элементов одинаковы, формула (4.5.8) принимает вид

Р = 1 - (1-р)ⁿ. (4.5.9)

Пример 4.5.5. Предохранительное устройство, обеспечивающее безопасность работы системы под давлением, состоит из трех дублирующих друг друга клапанов. Надежность каждого из них р=0,9. Клапаны независимы в смысле надежности. Найти надежность устройства.

Решение. По формуле (4.5.9) Р=1-(1-0,9)³=0,999.

Интенсивность отказов устройства состоящего из n параллельно соединенных элементов, обладающих постоянной интенсивностью отказов λ₀, определяется как

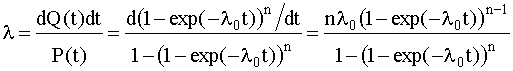. (4.5.10)

Из (4.5.10) видно, что интенсивность отказов устройства при n>1 зависит от t: при t=0 она равна нулю, при увеличении t, монотонно возрастает до λ₀.

Если интенсивности отказов элементов постоянны и подчинены показательному закону распределения, то выражение (4.5.8) можно записать

Р(t) = 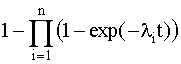. (4.5.11)

Среднее время безотказной работы системы Т₀ находим, интегрируя уравнение (4.5.11) в интервале [0,¥]:

Т₀=

=(1/ λ ₁+1/ λ ₂+…+1/ λ _n)-(1/( λ ₁+ λ ₂)+ 1/( λ ₁+ λ ₃)+…)+ (4.5.12)

+(1/( λ ₁+ λ ₂+ λ ₃)+1/( λ ₁+ λ ₂+ λ ₄)+…)+(-1)ⁿ⁺¹´ .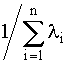

В случае, когда интенсивности отказов всех элементов одинаковы, выражение (4.5.12) принимает вид

Т₀= 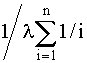. (4.5.13)

Среднее время работы до отказа также можно получить, интегрируя уравнение (4.5.7) в интервале [0,¥]

Пример 4.5.6. Предположим, что два одинаковых вентилятора в системе очистки отходящих газов работают параллельно, причем если один из них выходит из строя, то другой способен работать при полной системной нагрузке без изменения своих надежностных характеристик.

Требуется найти безотказность системы в течение 400ч (продолжительность выполнения задания) при условии, что интенсивности отказов двигателей вентиляторов постоянны и равны λ =0,0005ч^-1, отказы двигателей статистически независимы и оба вентилятора начинают работать в момент времени t=0.

Решение. В случае идентичных элементов формула (4.5.11) принимает вид

Р(t) = 2еxp(-λt) - еxp(-2λt).

Поскольку λ = 0,0005 ч^-1 и t = 400 ч, то

Р₍₄₀₀₎ = 2еxp(-0,0005´400) - еxp(-2´0,0005´400)=0,9671.

Среднюю наработку на отказ находим, используя (4.5.13):

Т₀= 1/λ(1/1 + 1/2) = 1/λ´3/2 = 1,5/0,0005 = 3000 ч.