Традиционный метод анализа

Итак, падение давления равно (при условии, что ВСС закончилось):

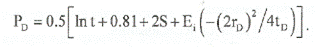
До тех пор, пока зона сжимаемости не достигает границы, параметр (2r_D)² /4t_D велик, и вторым слагаемым можно пренебречь:

То есть в начальные моменты времени пласт ведет себя как бесконечный.

Когда исследование продолжительно (математически - как только (2r_D)² /4t_D < 0.01), второе слагаемое может быть аппроксимировано логарифмической функцией:

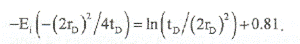
Таким образом, безразмерное давление может быть записано в виде:

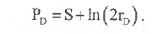
В реальных переменных падение давление равно:

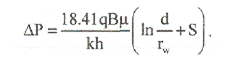
То есть давление в скважине остается постоянным, не зависит от времени.

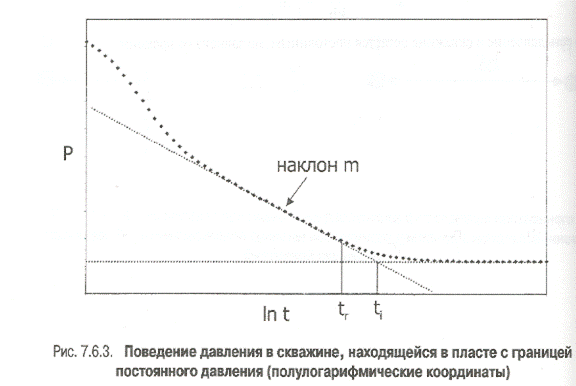
Так же, как в случае одной непроницаемой границы, можно использовать два метода, чтобы определить расстояние до границы постоянного давления:

· с использованием точки пересечения t_i; прямой линии наклона m на полулогрифмическом графике и горизонтальной прямой линии, соответствующей границе постоянного давления;

· с помощью понятия радиуса исследования.

Приравнивая два уравнения прямых линий, получим следующее уравнение для расстояния до границы постоянного давления:

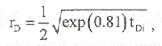
из которого имеем:

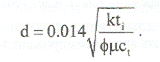
Если вторая прямая линия не достигается, для определения расстояния до границы можно использовать понятие радиуса исследования на момент t_r, когда данные по давлению покидают прямую линию наклона т:

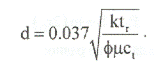
ЗАМКНУТЫЙ ПЛАСТ

До тех пор, пока зона сжимаемости не достигла границ пласта, пласт ведет себя как бесконечный, мы наблюдаем неустановившийся режим течения.

Когда пласт замкнутый и зона сжимаемости достигла всех границ, причем границы непроницаемые, режим течения становится псевдоустановившимся.

Непроницаемые границы определяют зону дренирования скважины.

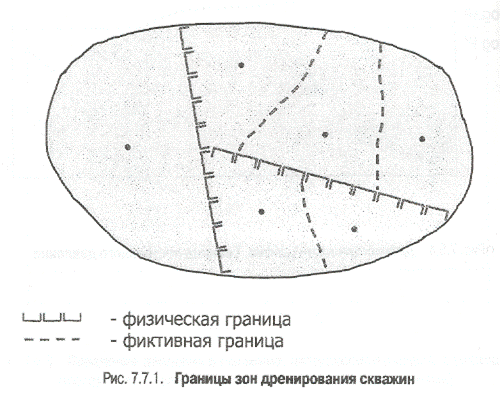
Границы зоны дренирования скважины могут представлять собой (рис. 7.7.1):

· физические барьеры: непроницаемые разломы, литологическое замещение и т.д.;

· фиктивные барьеры, возникающие в результате добычи из соседних скважин,

В соответствии с формулой Dietz положение границы между скважинами зависит от дебитов скважин и от эффективной мощности и пористости в каждой зоне дренирования:

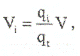
здесь V_j - поровый объем, дренируемый рассматриваемой скважиной;

q_j - дебит рассматриваемой скважины;

q, - общая добыча из пласта;

V - общий поровый объем.

С момента наступления псевдоустановившегося режима течения забойное давление меняется линейно со временем.

В безразмерных переменных зависимость давления от времени принимает вид;

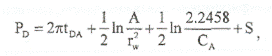
здесь t_DA = 0.00036 kt/jμс_tА ; А-площадь зоны дренирования; С_А - фактор фомы, который зависит от формы пласта и положения скважины в этом пласте,

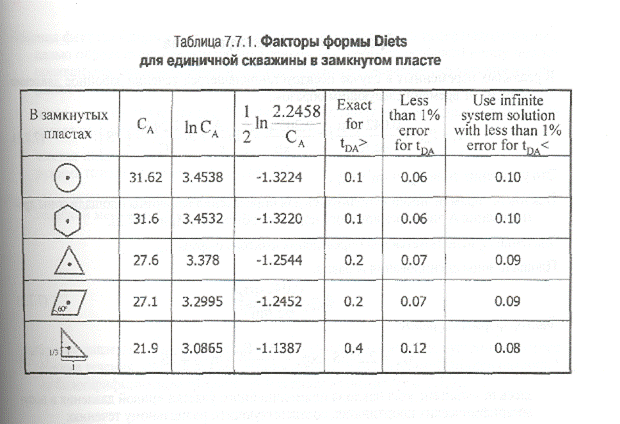
Существуют таблицы факторов формы, соответствующих различным конфигурациям пласта(табл. 7.7.1, приложение А1).

Так, например, для скважины, находящейся в центре кругового пласта, коэффициент С_А=31.62, и безразмерное давление принимает вид;

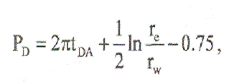
где 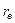- радиус зоны дренирования.

Из таблицы можно также заметить, что максимальное значение фактора формы соответствует круговому пласту со скважиной в центре. Маленькие значения С_А соответствуют вытянутым пластам со скважиной, смещенной относительно центра.