Традиционный метод анализа. Эффект влияния границы подобен эффекту влияния границы в бесконечном пласте: на графике в координатах (

Эффект влияния границы подобен эффекту влияния границы в бесконечном пласте: на графике в координатах ( 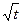, Р) появляется второй прямолинейный участок удвоенного наклона (рис. 7.4.2 Б). Такое явление наблюдается не всегда: только в случае, когда расстояние до границы канала от скважины намного больше ширины канала (a>>l} (рис. 7.4.2 А).

Уравнение второй линии в безразмерном виде;

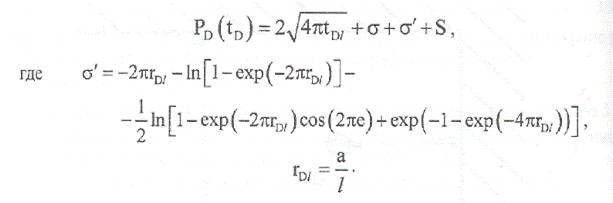
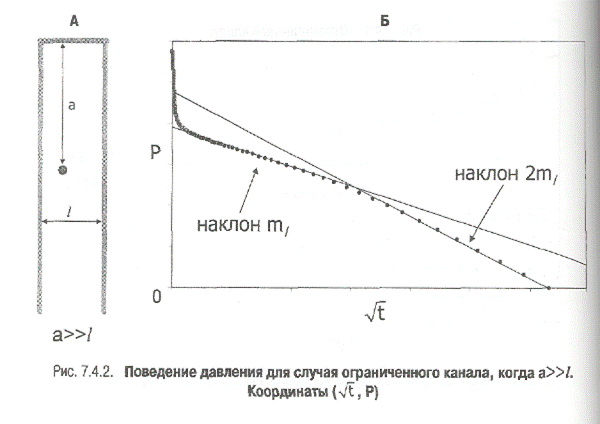
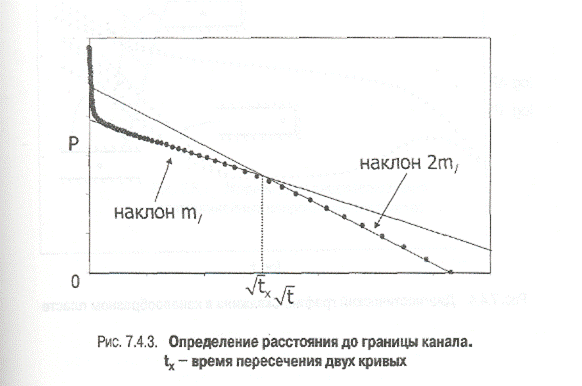
Расстояние до границы может быть получено путем нахождения точки пересечения двух прямых линий.

Приравнивая два уравнения, получаем:

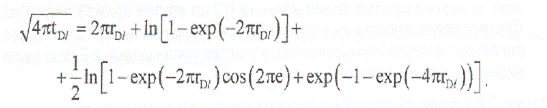
Это уравнение не решается в явном виде относительно r_Dl, за исключением случаев, когда а>>l и последними двумя слагаемыми можно пренебречь. Тогда получаем выражение:

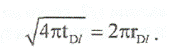
Выражая в размерных единицах относительно расстояния, имеем;

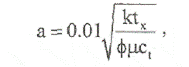
где k - проницаемость, [милидарси]; t_x - время пересечения двух прямых линий (рис. 7.4.3), [часы]; j - пористость; μ - вязкость, [спз]; c_t - общая сжимаемость. [am^-1].

Производная

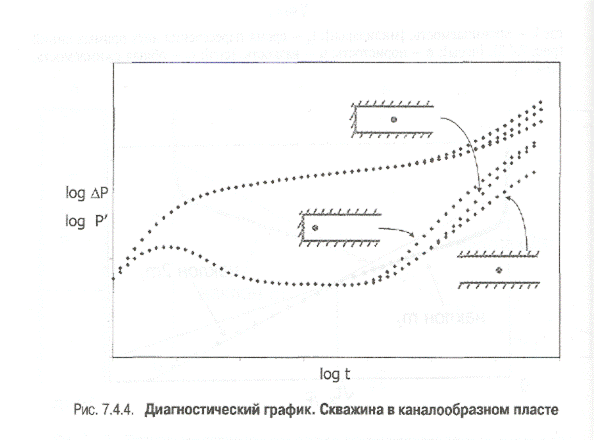
В случае ограниченного канала производная давления на билогарифмическом графике идет от первой прямой линии наклона 1/2 ко второй прямой линии наклона 1/2. Дублирование наклона на специализированном графике (Р от t^1/2) соответствует смещению второго прямолинейного участка производной в 2 раза вверх в билогарифмических координатах.

На рис. 7,4.4 приведены три вида типовых кривых в зависимости от расстояния от скважины до границы канала.

Когда граница очень близко расположена к скважине, производная, прежде чем установиться на прямой линии наклона 1/2, резко возрастает вверх (с наклоном > 1/2}. Эта особенность используется для диагностики границы в каналообразном пласте.

— 7.5. ДВЕ ПЕРЕСЕКАЮЩИЕСЯ ЛИНЕЙНЫЕ ГРАНИЦЫ

Иногда в течение исследования в скважине могут быть обнаружены две пересекающиеся непроницаемые границы, например два разлома (рис. 7,5,1).

Данные давления могут быть использованы для нахождения угла Θ между границами и расстояний от скважины до границ.