Традиционный метод анализа. Если во время исследования зона сжимаемости достигает обе пересекающиеся под углом Θ непроницаемые границы

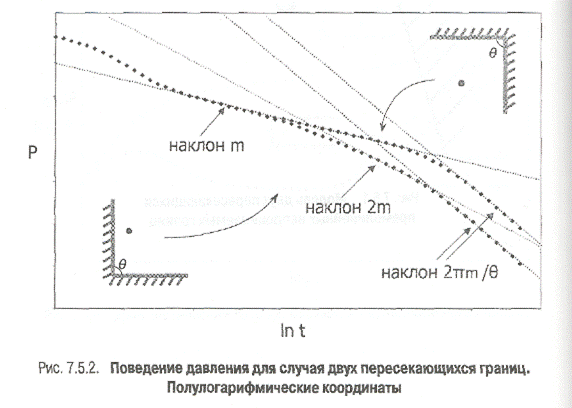
Если во время исследования зона сжимаемости достигает обе пересекающиеся под углом Θ непроницаемые границы, то данные по давлению, представленные в полулогарифмическом масштабе, будут обнаруживать два прямолинейных участка, один из которых, наклона m ₁=m, соответствует радиальному течению в пласте. Второй участок, наклона m₂=2pm/Θ, соответствует ситуации, когда обе границы влияют на приток к скважине (рис. 7.5.2).

Если скважина расположена ближе к одной из границ, на полулогарифмическом графике между двумя прямолинейными участками может появиться еще один прямолинейный участок наклона 2тm соответствующий влиянию одной непроницаемой границы в пласте (рис. 7.5.2),

Угол между двумя пересекающими границами может быть определен из соотношения наклонов двух прямолинейных участков:

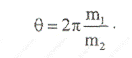
Расстояние от скважины до ближайшей границы может быть определено через понятие радиуса исследования или с помощью координаты точки пересечения двух прямых, как было описано ранее.

Производная

Поскольку логарифмическая производная давления - это тангенс угла наклона в полулогарифмических координатах, то каждый прямолинейный участок в этих координатах соответствует стабилизации производной в билогарифмических координатах.

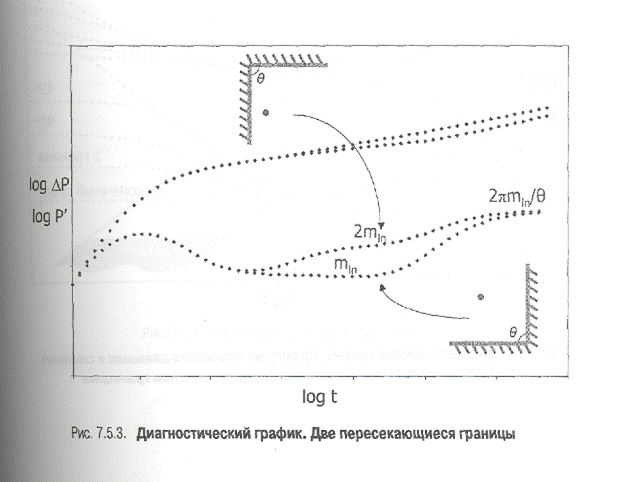
Значит, если скважина расположена в пласте с двумя пересекающимися под углом Θ границами, то график производной в конце концов будет стабилизироваться на величине 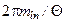(рис. 7.5.3).

Если скважина расположена намного ближе к одной из границ, кривая производной, перед тем как стабилизироваться на величине 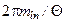, выйдет на «плато производной» со значением 2m_ln (рис. 7.5.3).

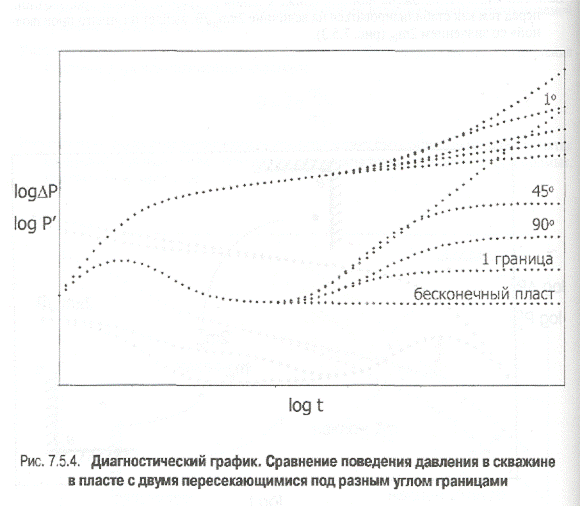
Когда угол между границами очень маленький, границы можно считать практически параллельными. Поведение давления в скважине будет очень похожим на поведение давления в скважине, расположенной в каналообразном пласте (рис. 7.5.4).

Переходное течение между стабилизацией на величинах m_ln и 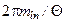соответствует квазилинейному течению с производной, возрастающей линейно с наклоном 0,5.