Традиционный метод анализа. Когда ВСС неощутимо, падение давления в скважине записывается следующим образом

Когда ВСС неощутимо, падение давления в скважине записывается следующим образом

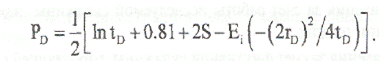
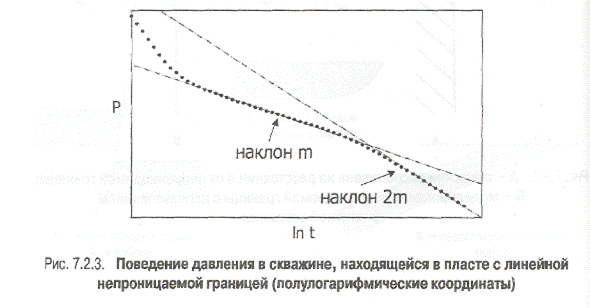
До тех пор, пока зона сжимаемости не достигла границы, (2r_D)² /4t_D велико, и Ei-функция практически равна нулю. Пласт ведет себя как бесконечный (прямая линия наклона m на полулогарифмическом графике) (рис. 7.2.3), падение давления равно:

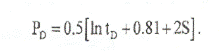
Когда зона сжимаемости достигает границы, второе слагаемое, соответствующее фиктивной скважине, нельзя считать нулевым. Давление падает быстрее, чем в бесконечном пласте, и точки измерения отклоняются от прямой линии на полулогарифмическом графике.

Когда (2r_D)²/4t_D < 0.01 (время t велико), Ei-функция может быть аппроксимирована логарифмом:

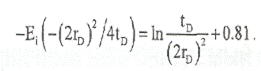
Таким образом, падение давления в скважине равно:

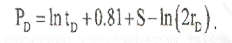
Если исследование продолжительное, непроницаемая граница будет проявляться как вторая прямая линия двойного наклона 2т на полулогарифмическом графике (рис.7.2.3).

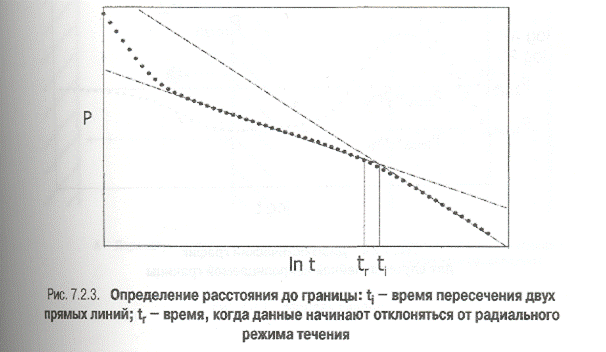
Расстояние до границы можно определить с помощью традиционного метода анализа. Данные давления наносятся на график как функция логарифма времени.

Если на полулогарифмическом графике видны два прямолинейных участка, то расстояние до границы можно определить с использованием точки пересечения этих прямых линий t_i(рис. 7.2.3).

Приравниваем два уравнения прямых линий:

Выражая r_D и заменяя безразмерные переменные размерными, получаем:

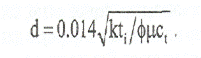(7.2.1)

Если исследование недлительное и второй прямолинейный участок не достигается на полулогарифмическом графике, то для оценки расстояния до границы можно использовать понятие радиуса исследования в момент времени t_r, когда точки измерения начинают отклоняться от первого прямолинейного участка:

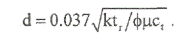(7-2.1)

где k -проницаемость [миллидарси]; t - время, [часы]; (р - пористость; μ - вяз­кость [спз]; c_t - общая сжимаемость [1/атм]; r_w - радиус скважины [м].

Замечание: Определение расстояния через радиус исследования может быть использовано для любого вида границы или неоднородности в пласте, однако этот метод менее точный и не позволяет определить характер границы.

Производная

Присутствие непроницаемой границы характеризуется появлением второго прямолинейного участка с двойным наклоном на полулогарифмическом графике.

Каждому прямолинейному участку на полулогарифмическом графике соответствует стабилизация производной давления на билогарифмическом графике с ординатой, равной тангенсу угла наклона в полулогарифмических координатах.

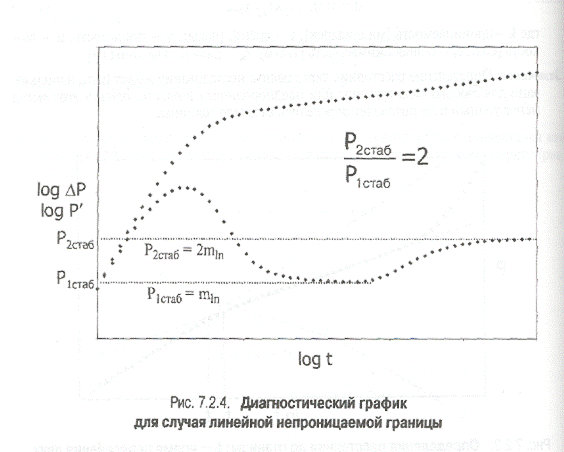
Поэтому характеристической особенностью непроницаемой границы является вторая стабилизация производной со значением 2m_ln (рис. 7.2.4).

Время t_r, когда производная «покидает» первое плато, соответствующее радиальному течению в пласте, можно использовать в формуле для нахождения расстояния до границы через радиус исследования. Определение t_r с помощью производной будет более аккуратным, чем его определение на полулогарифмическом графике.

КАНАЛ

Математической модели системы, называемой «канал», соответствуют две бесконечные непроницаемые границы, параллельные друг другу.

Данной модели могут соответствовать следующие реальные ситуации:

· два параллельных непроницаемых разлома;

· песчаные тела вытянутой формы (бары, каналы рек);

· смена разных фаций, параллельных друг другу по простиранию, и т.п.

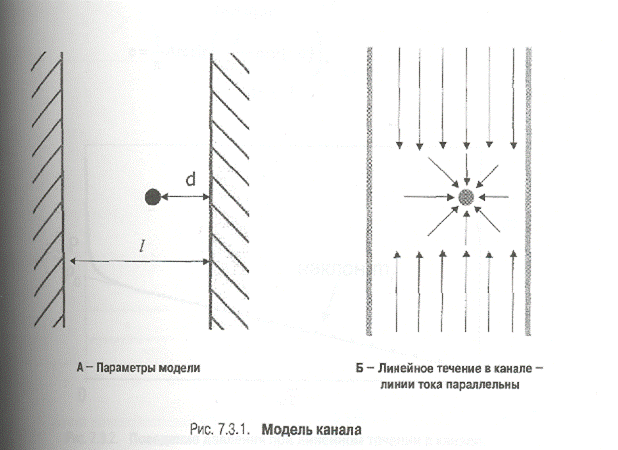
Канал определяется шириной 1 и расстоянием d от скважины до ближайшей из границ (рис. 7.3.1 А).

В течение исследования в скважине, находящейся в канале, несколько режимов течения сменяют друг друга:

· ВСС;

· радиальное течение;

· влияние ближайшей границы (наблюдается, если скважина сильно смещена относительно центра канала);

· линейное течение (рис. 7.3.1 Б).

Характеристическая или специальная функция для линейного течения - квадратный корень из времени. То есть в течение линейного режима течения давление на забое скважины линейно зависит от квадратного корня из времени:

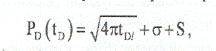
здесь t_Dl, =0.00036 kt/jμc_tl²- безразмерное время, вычисленное по отношению к ширине канала l, s = In (l/27pr_w ) - In (sin pe) - величина, характеризующая сме- iщение скважины относительно оси симметрии, e = d/l - эксцентриситет скважины.

В размерных единицах измерения решение имеет вид:

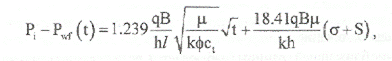(7.3.1)

где Р - давление [атм]; q - дебит, [м3/сут]; В - объемный коэффициент; μ - вяз­кость [спз]; k -проницаемость [миллидарси]; h - мощность [м]; t - время, [часы]; j - пористость; c_t - общая сжимаемость [1/атм]; r_w - радиус скважины [м].