Обобщенное спектральное представление сигналов

Литература: [Л.1], с 29-34

[Л.2], с 32-39

При рассмотрении геометрического представления сигналов мы зафиксировали пространство в какой-то момент времени 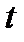. Снимем это ограничение и будем полагать, что каждый вектор 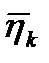координатного базиса представляет собой функцию времени 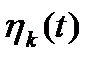. Переходя к функциям времени выражение (1.31) можно переписать следующим образом применительно для функций координатного базиса 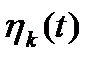и

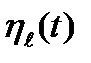
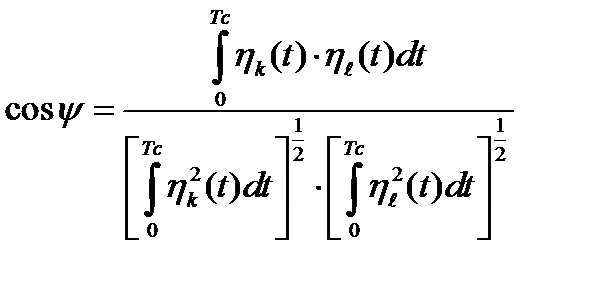, (1.32)

Но вектора 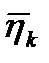и 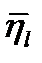взаимноперпендикулярны, т.е. угол между ними составляет 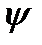=90⁰, а .

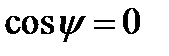Приравнивая (1.32) к нулю и учитывая, что нормы 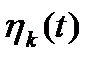и 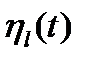всегда отличны от нуля, получим:

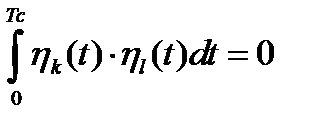. (1.33)

Две функци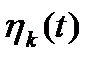и и 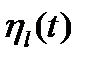, скалярное произведение (1.33) которых равно нулю, называют ортогональными функциями. Таким образом, декартова система координат при геометрическом представлении соответствует системе ортогональных функций 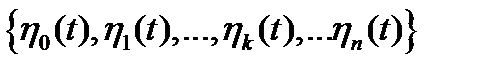. Поскольку по определению

,

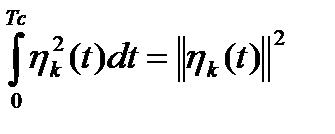то система функций 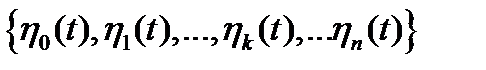является ортогональной, если выполняется условие

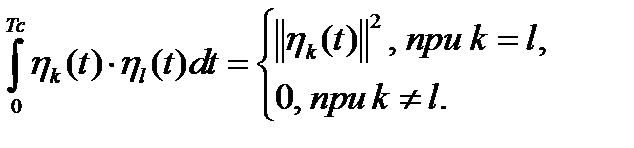(1.34)

При выполнении условия

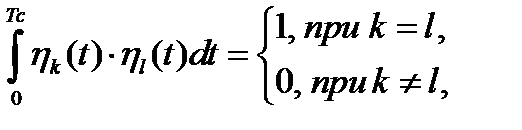(1.35)

система функций называется ортонормированной. Нетрудно убедиться, что нормировка осуществляется делением каждой функции 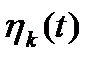на ее норму. С геометрической точки зрения каждая функция ортонормированной системы соответствует единичному вектору – орту.

С учетом вышеизложенного при условии конечной энергии сигнала на интервале (0,Тс), т.е.

,

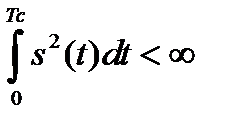выражение (1.20) можно записать следующим образом

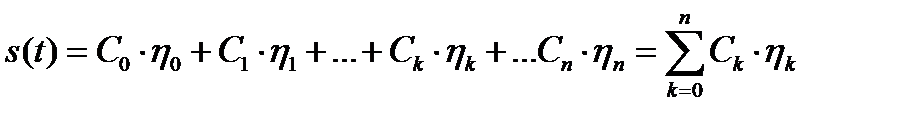. (1.36)

Выражение (1.36) представляет собой разложение сигнала 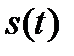на составляющие в системе ортогональных базисных функций (в ортогональном базисе) и называется обобщенным рядом Фурье.

Если число ортогональных функций в базисе 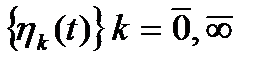бесконечно, то обобщенный ряд Фурье описывается следующим выражением

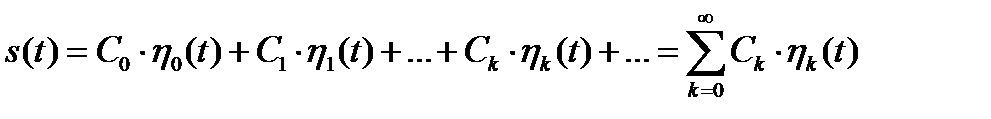. (1.37)

В дальнейшем мы будем пользоваться именно таким представлением обобщенного ряда Фурье.

Для определения значений 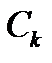умножим обе части (1.37) на 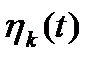и проинтегрируем произведение в пределах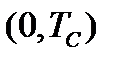

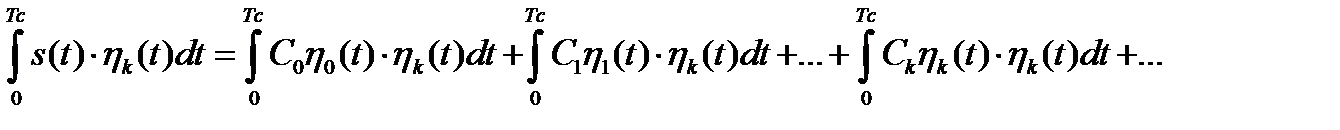(1.38)

В силу ортогональности функций 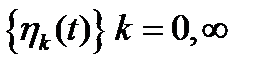все слагаемые в (1.38) будут равны нулю кроме слагаемого, в котором индексы функций совпадают. Тогда выражение (1.38) примет следующий вид

.

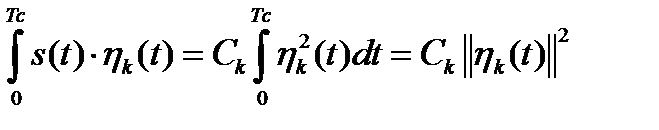Отсюда следует, что

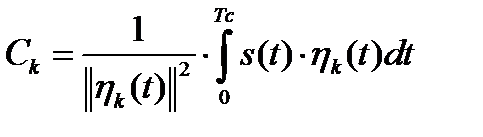. (1.39)

Отдельная функция 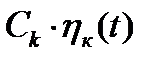называется спектральной составляющей сигнала, а совокупность коэффициентов 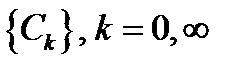носит название спектра сигнала в данной системе базисных функций. Спектр сигнала полностью определяет его свойства.

И, в заключение, выясним, как связаны между собой энергия сигнала в целом и его спектральных составляющие. Для простоты сначала положим, что сигнал 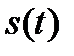представлен всего двумя спектральными составляющими

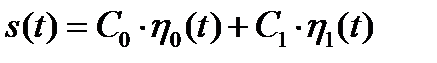. (1.40)

Так как энергия сигнала

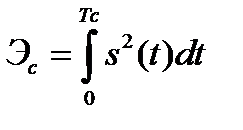, (1.41)

то, подставляя (1.40) в (1.41), получим

.

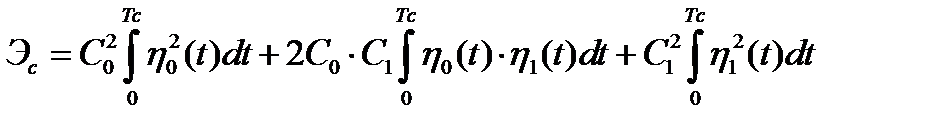В силу ортогональност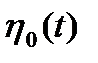и и 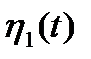второе слагаемое будет равно нулю. Тогда энергию сигнала можно представить формулами

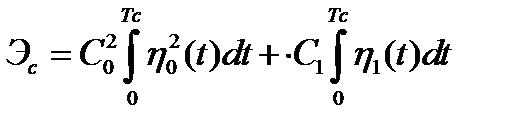
или

.

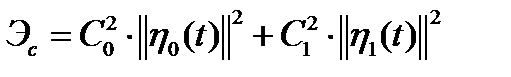Распространяя полученный результат на систему ортогональных функций 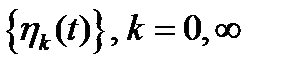, получим

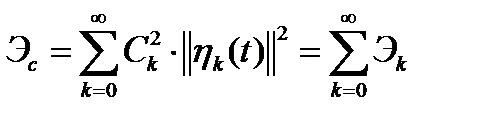, (1.42)

Где 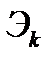– энергия k-той составляющей.

Если 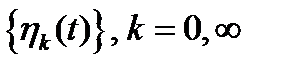- система ортонормированных функций, то (1.42) принимает вид:

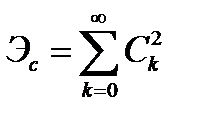. (1.43)

Выражения (1.42) или (1.43) представляют собой равенство Парсеваля, которое означает, что энергия сигнала 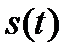равна сумме энергий всех спектральных составляющих. То же самое справедливо и для средней мощности сигнала.

Итак, выражения (1.36) и (1.37) не конкретизируют вид функций 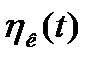. В качестве таких функций в радиотехнике рассматриваются тригонометрические функции, функции Уолша, Хаара и ряд других. Поэтому перейдем к рассмотрению спектрального анализа сигналов в конкретных базисных системах.