Динамическое представление сигналов

Литература: [Л.1], с 16-22

[Л.2], с 26-30

[Л.3], с 4-7

При построении РТИС возникают задачи анализа и синтеза радиотехнических сигналов. Сущность анализа состоит в том, что изучаемый объект разбивается на составные части, после чего проводится их исследование. Применительно к радиотехническим сигналам при анализе исследуемый сигнал описывается совокупностью других более простых сигналов с хорошо изученными свойствами. Такое представление позволяет, с одной стороны, сложную задачу преобразования исследуемого сигнала радиотехническими устройствами свести к задачам преобразования известных сигналов, а с другой стороны, - достаточно эффективно решать задачи синтеза сигналов с заданными свойствами.

Как уже подчеркивалось выше, в общем случае сигнал 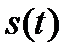описывается функцией времени, позволяющей рассматривать сигнал как процесс, развивающейся во времени. Поэтому представление сигнала 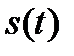сложной формы совокупностью простых сигналов, также описываемых функциями времени, получило название динамического или временного представления.

В теории радиотехнических сигналов для динамического представления используются следующие элементарные функции: функция знака 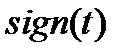(сигнум-функция), единичная функция 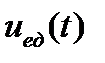(функция включения, функция Хевисайда), дельта-функция 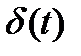(функция Дирака) и прямоугольный импульс с единичной высотой 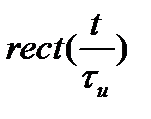(рис. 1.5, а, б, в, г). Рассмотрим вид этих функций и способы представления радиотехнических сигналов этими функциями.

Функция знака 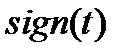имеет постоянную величину, равную единице, знак которой изменяется скачком при переходе переменной 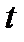через ноль (рис. 1.5, а). Математически функция знака описывается выражением

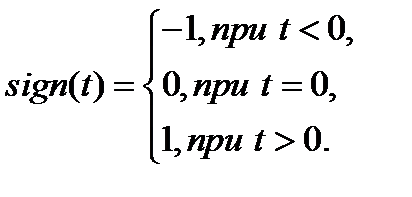(1.8)

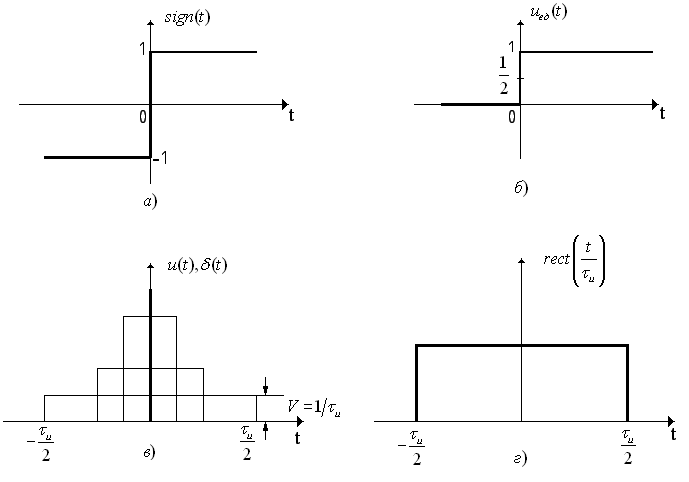
Рис. 1.5

Умножение на 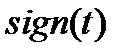означает изменение знака сигнала в момент времени .

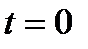Единичная функция 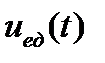характеризует собой единичный скачок при переходе через ноль (рис.1.5, б). Математическое выражение единичной функции имеет следующий вид

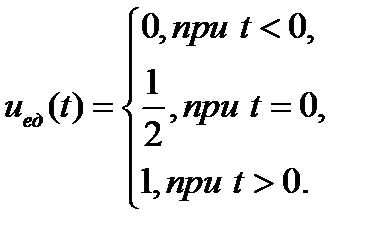(1.9)

Умножение 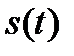на 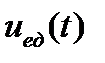равносильно включению этого сигнала в момент времени 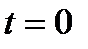. Сравнивая (1.8) и (1.9) можно установить, что

.

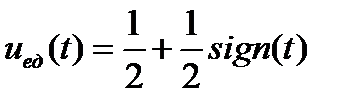Дельта-функция 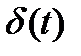была введена физиком-теоретиком П. Дираком. Рассмотрим импульс 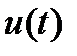единичной площади и длительностью 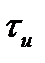(рис. 1.5, в)

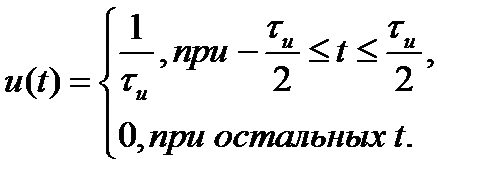
Будем уменьшать длительность импульса при сохранении его площади, равной единице. При этом высота импульса 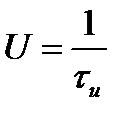будет возрастать. При 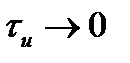высота импульса будет стремиться к бесконечности. Это и есть 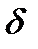- функция (на рисунке выделена утолщенным отрезком со стрелкой)

.

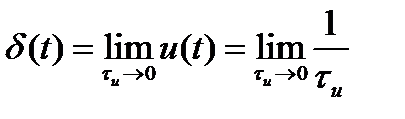Математически 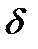-функция записывается следующим образом

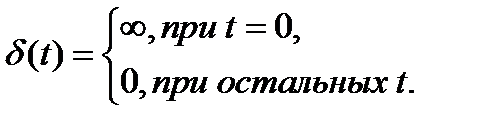(1.10)

Сравнивая (1.9) и (1.10) нетрудно установить, что

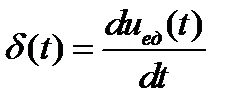(1.11)

Отметим некоторые свойства 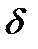- функции.

Так как исходный импульс 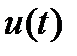описывается четной функцией, то 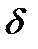- функция тоже четная, т.е.

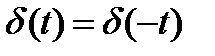
Во-вторых, ввиду того, что площадь исходного импульса равна единице, т.е.

,

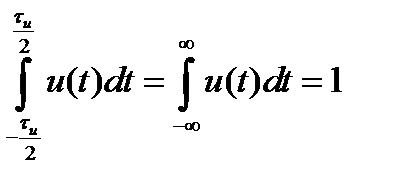поэтому .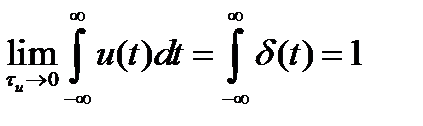

И наконец, отметим фильтрующее свойство - функции

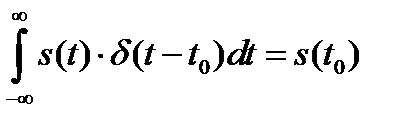. (1.12)

Иными словами интеграл произведения на 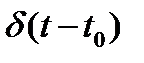равен значению 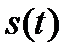в момент времени .

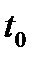Прямоугольный импульс с единичной амплитудой (рис. 1.5, г) описывается следующим выражением

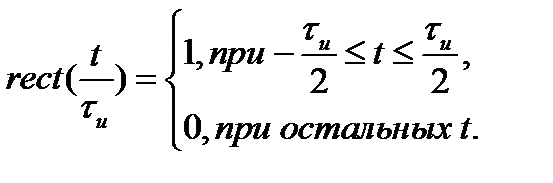(1.13)

С помощью прямоугольного импульса с единичной высотой можно достаточно просто описать периодическую последовательность прямоугольных импульсов, цифровые сигналы в виде двоичных кодовых комбинаций и другие.

Рассмотрим теперь каким же образом сигнал произвольной формы 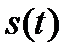можно описать с помощью рассмотренных выше элементарных функций. На практике для такого представления используются единичная функция и 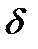- функция.

Возьмем сигнал произвольной формы 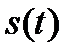и приближенно представим его ступенчатой функцией, которая изменяется в моменты времени 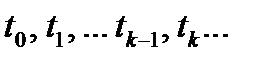, отстоящие друг от друга на равные интервалы времени 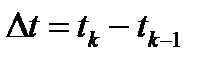(рис. 1.6).

Пусть в момент времени 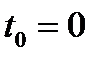сигнал принимает значение 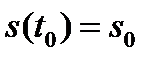. Тогда на интервале времени 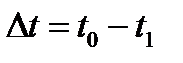значение сигнала можно представить в виде произведения

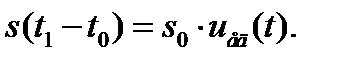
Рассмотрим интервал времени 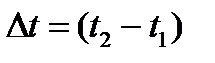. Значение сигнала в мо-мент времени 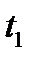очевидно равно 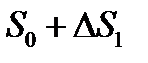, где .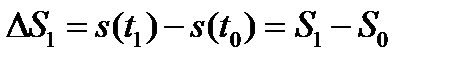

С другой стороны, величину 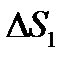можно представить в виде произведения

.

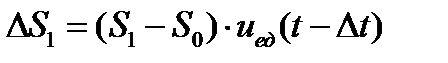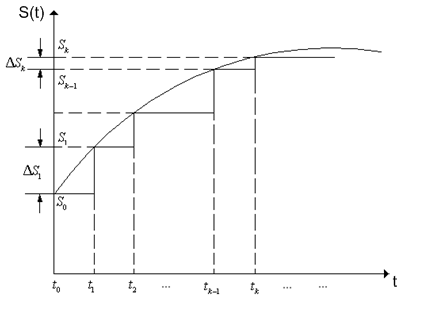
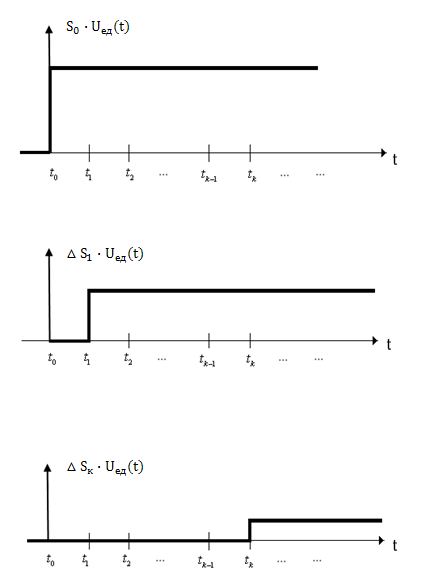
Рис. 1.6

Тогда значение сигнала в момент времени 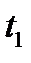запишется следующим образом

.

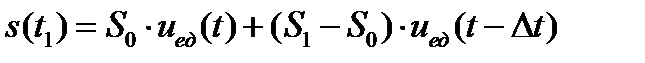Продолжая аналогичные рассуждения, получим

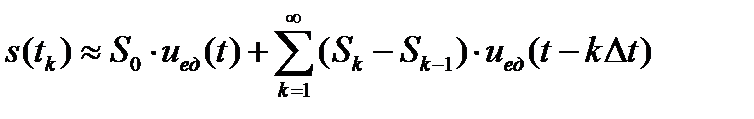. (1.14)

Очевидно, с уменьшением 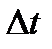точность представления сигнала возрастает.

Если разделить обе части равенства (1.14) на 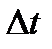и устремить 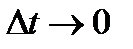, можно получить точное выражение сигнала при его представлении совокупностью единичных функций

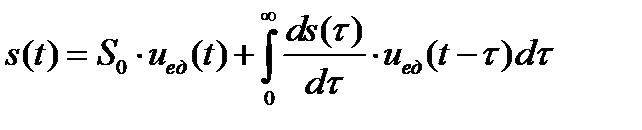. (1.15)

Перейдем к рассмотрению представления сигнала 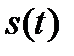посредством 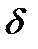- функции. Для этого представим сигнал в виде суммы прямоугольных импульсов длительностью 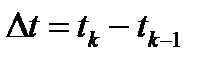и высотой 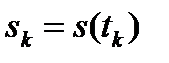(рис. 1.7).

Рассмотрим интервал времени 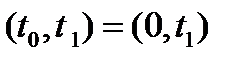. Очевидно, импульс на этом интервале времени можно представить следующим образом:

.

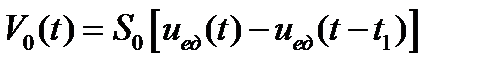На произвольном интервале времени 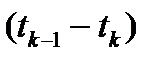импульс:

.

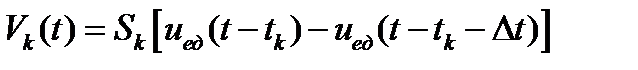Тогда сигнал, представленный в виде суммы прямоугольных импульсов, приближенно можно описать следующим выражением:

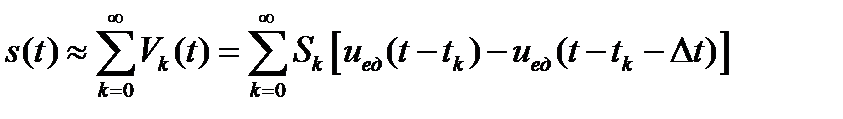. (1.16)

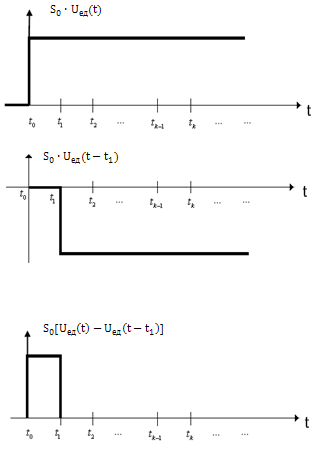
Рис. 1.7

Так же, как и в предыдущем случае, сигнал будет представлен тем точнее, чем меньше длительность импульсов . Разделив и умножив правую часть (1.16) на 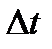, получим

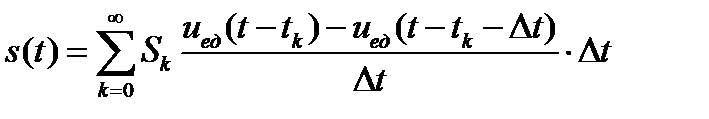. (1.17)

Устремим 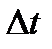к нулю. Тогда суммирование в (1.17) можно заменить интегрированием по новой переменной 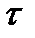, дифференциал которой 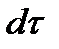будет соответствовать .

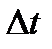Поскольку

,

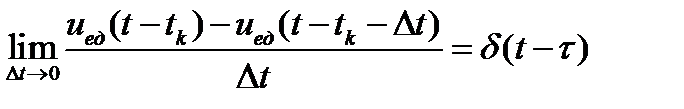выражение (1.17) примет следующий вид

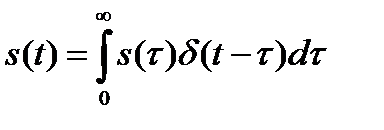. (1.18)

Распространяя область определений сигнала на всю ось действительных чисел, т.е. 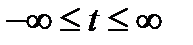, окончательно получим

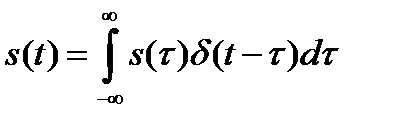. (1.19)

Итак, если сигнал 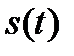умножить на 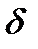- функцию и произведение проинтегрировать по времени, то результат будет равен значению сигнала в точке, где сосредоточен дельта-импульс. Выражение (1.19) как раз и отображает фильтрующее свойство 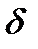- функции.