Иррациональные числа

Математикам Древней Греции были известны лишь рациональные числа. К ним относятся все целые числа, например, 1, 2, 3 и т. д. или целочисленные дроби – 1/2, 2/3 и т. п. Если отношение длин двух отрезков выражалось целочисленной дробью, древнегреческий математик считал, что они «соизмеримы». К примеру, если они находятся в отношении 3/5, это означает, что если один из этих отрезков отложить три раза, а другой пять раз, то получится два отрезка одинаковой длины. Представьте себе потрясение античных математиков, выяснивших, что не все отрезки являются соизмеримыми. Например, в прямоугольном равнобедренном треугольнике гипотенуза несоизмерима ни с одним из двух одинаковых катетов. В понятиях современной математики, поскольку, согласно теореме Пифагора квадрат гипотенузы такого треугольника равен удвоенному квадрату длины любого из катетов, длина гипотенузы равняется произведению длины любого из катетов на квадратный корень из 2. Это означает, что квадратный корень из 2 не является рациональным числом. Доказательство этого факта Евклидом в книге X «Элементов» базируется на первоначальном предположении обратного, что существует рациональное число, квадрат которого равен 2, после чего Евклид опровергает это предположение.

Допустим, что есть рациональное число, выраженное дробью p /q (где p и q – целые числа), чей квадрат равен 2:

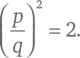
В таком случае будет бесконечное количество таких пар чисел, которые можно получить, умножая p и q на любой натуральный множитель, но предположим, что целые числа p и q – наименьшие целые, для которых верно выражение (p /q ) 2 = 2. Из уравнения выше следует, что

p ² = 2q ².

Отсюда очевидно, что p ² – четное число, но так как произведение двух любых нечетных чисел есть нечетное число, то p должно быть только четным. То есть мы можем записать равенство p = 2p ', где p ' – целое число. Но тогда

q ² = 2p '²

и, повторяя предыдущую цепь рассуждений, находим, что число q также четное и может быть выражено равенством q = 2q ', где q ' – целое число. Но тогда p /q = p '/q ', и значит,

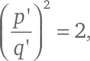
где p ' и q ' – целые числа, которые в два раза меньше p и q соответственно. А это противоречит исходному предположению, что p и q – наименьшие целые числа, для которых равенство (p /q )² = 2 справедливо. Мы имеем противоречие, и, следовательно, такие числа не могут существовать.

Теорема явным образом обобщается: любое число, например, 3, 5, 6 и т. д., которое само не является квадратом целого числа, не может быть квадратом рационального числа. Например, если 3 = (p /q )², где p и q – наименьшие целые числа, для которых это равенство справедливо, то p ² = 3q ², но это невозможно, если только нет такого целого p ', для которого p = 3p ', но тогда q ² = 3p '², и q = 3q ' для некоего целочисленного q ', и, значит, 3 =(p '/q ')², что противоречит предположению о том, что не существует целых чисел меньше p и q , для которых p 2 = 3q 2. Поэтому квадратные корни чисел 3, 5, 6, … иррациональны все.

Современная математика признает существование иррациональных чисел, таких как число, обозначаемое √2, квадрат которого равен 2. Если это число представить в виде десятичной дроби, то последовательность знаков такого числа продолжается до бесконечности, не повторяясь. Например, √2 = 1,414213562… И во множестве рациональных, и во множестве иррациональных чисел их количество бесконечно, но в каком‑то смысле иррациональных чисел намного больше, чем рациональных, поскольку рациональные числа можно представить как бесконечную последовательность, включающую все рациональные числа:

1, 2, 1/2, 3, 1/3, 2/3, 3/2, 4, 1/4, 3/4, 4/3, …

тогда как перечислить все иррациональные числа никаким способом нельзя.