Технические замечания
Приведенные ниже замечания объясняют научную и математическую основу многих исторических открытий, которые обсуждались в книге. Читатели, которые изучали алгебру и геометрию в старших классах школы и не полностью их забыли, не должны испытывать затруднений при чтении технических замечаний. Но я попытался организовать книгу таким образом, чтобы читатели, которые не интересуются техническими деталями, могли бы пропустить эти замечания и тем не менее понимать основной текст.
Хочу предупредить, что математический аппарат, используемый в замечаниях, не обязательно соответствует своему времени. От Фалеса до Ньютона стиль математики, применяющейся к решению физических задач, был куда более геометрическим и менее алгебраическим, чем это принято сегодня. Проанализировать эти задачи в таком геометрическом стиле было бы трудно для меня и утомительно для читателя. В этих замечаниях я покажу, как результаты, полученные натурфилософами прошлого, были дополнены (или, в некоторых случаях, не были) наблюдениями и предположениями, на которые они опираются, но я не буду пытаться достоверно воспроизвести детали всех рассуждений.
1. Теорема Фалеса
2. Платоновы тела
3. Гармония
4. Теорема Пифагора
5. Иррациональные числа
6. Установившаяся скорость падения
7. Падение капель
8. Отражение
9. Плавающие и погруженные в жидкость тела
10. Площадь круга
11. Размеры Солнца и Луны и расстояния до них
12. Размер Земли
13. Эпициклы внутренних и внешних планет
14. Параллакс Луны
15. Синусы и хорды углов
16. Горизонт
17. Геометрическое доказательство теоремы о средней скорости
18. Эллипсы
19. Элонгации и орбиты внутренних планет
20. Суточный параллакс
21. Правило равных площадей и эквант
22. Фокусное расстояние линзы
23. Телескоп
24. Лунные горы
25. Ускорение под действием силы тяжести
26. Параболические траектории
27. Вывод закона преломления света по аналогии с теннисным мячиком
28. Вывод закона преломления света на основе принципа наименьшего времени
29. Теория радуги
30. Вывод закона преломления света на основе волнового принципа
31. Измерение скорости света
32. Центростремительное ускорение
33. Сравнение Луны с падающим телом
34. Закон сохранения импульса
35. Массы планет
1. Теорема Фалеса[23]
Теорема Фалеса – хороший пример того, как, рассуждая в понятиях геометрии, можно прийти к неочевидному выводу о свойствах окружностей и треугольников. Фалес или кто‑либо другой был первым, кто доказал эту теорему, для нас она представляет интерес, так как демонстрирует, что древние греки знали о геометрии до Евклида.
Рассмотрим любую окружность. Пусть прямая пересекает ее по диаметру. Точки пересечения этой прямой с окружностью обозначим A и B . Выберем в любом месте окружности точку P , не совпадающую ни с A , ни с B , и соединим точки A и B с точкой P отрезками. Диаметр AB и отрезки AP и BP образуют треугольник ABP . Теорема Фалеса гласит, что такой треугольник всегда является прямоугольным, то есть его угол при вершине P всегда равен 90°.
Хитрость в доказательстве этой теоремы заключается в том, что необходимо из центра C окружности провести в точку P радиус CP . При этом треугольник ABP окажется разделен на два треугольника: ACP и BCP (см. рис. 1). Оба эти треугольника являются равнобедренными, то есть такими, у которых две стороны равны. В треугольнике ACP стороны CA и CP являются радиусами окружности и, по определению окружности, равны (будем обозначать стороны треугольника по точкам, которые они соединяют). Аналогично в треугольнике BCP равны стороны CB и CP . В равнобедренном треугольнике углы, противолежащие равным сторонам, равны между собой, поэтому угол α (альфа) между сторонами AP и AC равен углу между сторонами AP и CP , а угол β (бета) между сторонами BP и BC равен углу между сторонами BP и CP . Сумма углов любого треугольника равна удвоенному прямому углу[24], или, как сейчас принято говорить, 180°, поэтому если в треугольнике ACP третий угол между сторонами AC и CP обозначить α′ и точно так же обозначить β′ угол между сторонами BC и CP в треугольнике BCP , то будут верны равенства:
2α +α' = 180°; 2β+β' = 180°
Сложив оба равенства и переставив слагаемые местами, получим:
2(α + β)+ (α' + β') = 360°.
Учтем, что α′ + β′ – это развернутый угол между сторонами AC и BC , то есть такой угол, лучи которого образуют отрезок прямой линии. Его величина составляет 180°, поэтому:
2(α + β) = 360° − 180° = 180°.
Следовательно, α + β = 90°. Но если посмотреть на рисунок 1, то легко увидеть, что угол α + β – это угол между сторонами AP и BP в исходном треугольнике ABP, значит, он является прямоугольным треугольником, что и требовалось доказать.
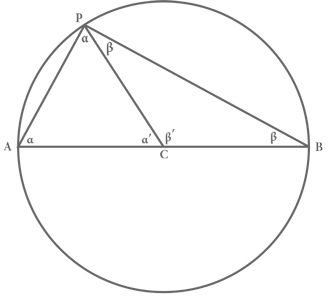
Рис. 1. Доказательство теоремы Фалеса. Теорема утверждает, что для любой взятой на окружности точки P угол между отрезками, проведенными из этой точки к концам произвольного диаметра AB , будет прямым.
Платоновы тела
В рассуждениях Платона о природе вещества центральное место занимает класс геометрических тел, известных как правильные многогранники, которые также известны как платоновы многогранники. Правильные многогранники можно рассматривать как трехмерную аналогию правильных многоугольников в планиметрии, и в определенном смысле они строятся из правильных многоугольников. Правильный многоугольник – это плоская фигура, ограниченная n одинаковыми отрезками, имеющая n вершин, причем углы, образуемые соседними сторонами при каждой вершине, равны. Например, правильными многоугольниками являются равносторонний треугольник (треугольник, все стороны которого равны) и квадрат. Правильный многогранник – это объемное тело, ограниченное одинаковыми правильными многоугольниками, причем все его вершины представляют собой равные телесные углы, стороны которых образованы N равными многоугольниками‑гранями.
Самый привычный пример правильного многогранника – это куб. Куб образуют шесть одинаковых граней‑квадратов, в каждой из его восьми вершин смыкаются три квадратные грани. Есть еще более простой правильный многогранник, тетраэдр: это треугольная пирамида, образованная четырьмя одинаковыми равносторонними треугольниками, у него четыре вершины, в каждой их которых смыкаются три треугольные грани. (Мы рассматриваем только выпуклые многогранники, у которых каждая вершина направлена наружу – к ним относятся и куб, и тетраэдр.) Из текста «Тимея» понятно, что Платон откуда‑то знал о том, что может быть лишь пять различных видов таких правильных многогранников, и он посчитал, что атомы различных форм материи имеют форму именно этих многогранников. Пять правильных многогранников включают тетраэдр, куб, октаэдр, додекаэдр и икосаэдр с 4, 6, 8, 12 и 20 гранями соответственно.
Сохранившееся со времен античности свидетельство о самой ранней попытке доказать, что существует лишь пять правильных многогранников, имеется в финальной, кульминационной части «Начал» Евклида. В предложениях 13–17 книги XIII Евклид описывает геометрическое строение тетраэдра, октаэдра, куба, икосаэдра и додекаэдра. Затем он пишет: «Вот я утверждаю, что, кроме упомянутых пяти тел, нельзя построить другого тела, заключенного между равносторонними и равноугольными равными друг другу <многоугольниками>» [25]. Н а самом деле после этого утверждения Евклид доказывает более узкую теорему о том, что в правильном многограннике существует только пять возможных комбинаций количества сторон n у каждой многоугольной грани и количества N смежных в каждой вершине многоугольников. Ниже приведено доказательство, аналогичное евклидову, но с использованием современной терминологии.
На первом шаге необходимо рассчитать внутренний угол θ (тета) каждой из n вершин n ‑стороннего правильного многоугольника. Проведем лучи из центра многоугольника к каждой из его вершин. В результате многоугольник окажется разделен на n треугольников. Поскольку сумма углов треугольника равна 180° и в каждом из этих треугольников есть по два угла, равных θ/2, то угол при третьей вершине, совпадающей с центром многоугольника, равняется 180° – θ. Так как n таких углов должны составлять полный угол 360°, то n (180° – θ) = 360°. Решая это уравнение, получаем:

К примеру, для равностороннего треугольника имеем: n = 3, поэтому θ = 180° – 120° = 60°, тогда как для квадрата n = 4, и θ = 180° – 90° = 90°.
На втором шаге представим себе, что мы отрезали от нашего многогранника все грани, ребра и вершины, кроме тех, которые примыкают к какой‑то одной выбранной вершине. Теперь то, что получилось, мысленно поставим на плоскость и «раздавим», нажав на эту вершину. Теперь N многоугольников, которые смыкались (были смежными) в этой вершине, окажутся лежащими на плоскости, но между ними должно остаться пустое место – в противном случае, если бы они покрывали полный угол, N многоугольников формировали бы слитную плоскую фигуру. Поэтому очевидно, что справедливо неравенство: N θ < 360°. Подставив вместо θ приведенную выше формулу и поделив обе части неравенства на 360°, получаем:
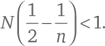
или, что то же самое (если обе части разделить на N ):

Учтем, что должно выполняться условие n ≥ 3, поскольку это минимальное количество вершин для многоугольника, и также должно выполняться неравенство N ≥ 3, так как иначе в многограннике не оставалось бы места между смежными при вершине многоугольными гранями (например, для куба n = 4, потому что грани квадратные, а N = 3). Поэтому вышеприведенное неравенство не позволяет ни отношению 1/n , ни отношению 1/N быть слишком малым, например, 1/2 – 1/3 = 1/6. Соответственно, ни n , ни N не могут быть равными или больше 6. Зная это, легко проверить все возможные комбинации целых чисел в диапазонах 5 ≥ N ≥ 3 и 5 ≥ n ≥ 3 на соответствие неравенству и обнаружить, что есть только пять таких комбинаций:
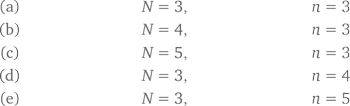
(В случаях, когда n равняется 3, 4 и 5, мы имеем стороны правильного многогранника, которые являются равносторонними треугольниками, квадратами и пятиугольниками соответственно.) Именно эти значения N и n присутствуют в тетраэдре, октаэдре, икосаэдре, кубе и додекаэдре.
Вот и все, что доказал Евклид. Но он не доказал, что существует лишь по одному правильному многограннику для каждой возможной пары n и N . Теперь мы пойдем дальше Евклида и покажем, что для каждой пары значений n и N мы получим по единственной комбинации других свойств многогранника: F – количества граней, E – количества ребер, и V – количества вершин. Как мы видим, есть три неизвестные величины, и значит, чтобы их найти, нам потребуется три уравнения. Чтобы вывести первое, отметим, что общее количество сторон всех многоугольников, образующих поверхность многогранника, равняется nF , но при этом каждая из Е граней является общей границей двух соседних многоугольников, поэтому:
2 E = nF.
Также учтем, что N граней пересекаются в каждой из V вершин, и притом каждое из E ребер соединяет две вершины, так что:
2 E = NV.
И наконец, есть и еще одно, менее явное, соотношение между величинами F, E и V . Чтобы его вывести, нужно принять дополнительное допущение – пусть наш многогранник является односвязным, то есть любой путь, который можно проложить между двумя различными точками его поверхности, можно непрерывно преобразовать в любой другой путь между теми же самыми точками. Это условие выполняется, например, для куба и тетраэдра, но не для многогранника (неважно, правильного или нет), который получили, разместив его вершины и грани вдоль поверхности тора. Существует сложная теорема, которая доказывает, что любой односвязный многогранник можно получить, если последовательно добавлять новые ребра, грани и/или вершины к тетраэдру, а потом сжать получившуюся фигуру до нужной формы. Зная об этом, мы покажем, что любой односвязный многогранник (правильный или неправильный) удовлетворяет равенству:
F – E + V = 2.
Легко проверить, что равенство удовлетворено для тетраэдра, в случае которого F = 4, E = 6 и V = 4, поэтому в левой части уравнения имеем: 4–6 + 4 =2. Если теперь мы добавим к любому многограннику ребро, секущее какую‑либо из его граней от одного ребра до другого, то у нас добавится одна дополнительная грань и две дополнительные вершины, а значит, величины F и V увеличатся на единицу и двойку, соответственно. Но оба из прежних ребер, в которые упирается новое ребро, при этом еще окажутся разбиты на два, и поэтому E увеличится на 1 + 2 =3, и выходит, что соотношение F – E + V останется неизменным. Точно так же, если мы добавим новое ребро, которое пролегает между какой‑либо вершиной и точкой, принадлежащей одному из имеющихся ребер, то мы увеличим F и V на единицу, а E при этом на 2, и значит, формула F – E + V все равно даст тот же результат. Поскольку любой односвязный многогранник может быть построен произвольной комбинацией этих действий, все получающиеся многогранники должны сохранять то же самое соотношение, то есть для них выражение F – E + V = 2 будет так же справедливо, как и для тетраэдра (это простой пример того, чем занимается отрасль математики под названием «топология»; в топологии число, выражаемое формулой F – E + V , называется эйлеровой характеристикой полиэдра, или многогранника).
Теперь мы можем совместно решить все три уравнения для E, F и V . Проще всего использовать первые два уравнения, чтобы заменить F и V в третьем на выражения, соответственно, 2E /n и 2E /N , и, таким образом, третье уравнение выражается в форме 2E /N – E +2E /N =2, что дает
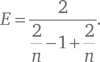
Далее из двух других уравнений получаем:

И теперь для пяти вышеперечисленных случаев количество граней, вершин и ребер будет равно:

Это и есть платоновы тела.
Гармония
Пифагорейцы открыли, что две струны щипкового музыкального инструмента одной и той же толщины, сделанные из одинакового материала и одинаково сильно натянутые, когда их щипают одновременно, производят приятный слуху звук, если отношение длин двух таких струн выражается как дробь с небольшим целым числителем и знаменателем – например, 1/2, 2/3, 1/4, 3/4 и т. д. Чтобы понять, почему так происходит, сперва нам нужно выяснить, как связаны друг с другом частота, длина и скорость распространения для любого вида волн.
Любая волна – это процесс распространения колебаний. В случае акустической (звуковой) волны в воздухе распространяются колебания давления воздуха, в случае волны на поверхности моря распространяются колебания толщины воды, в случае световой волны определенной поляризации колеблется вектор напряженности электрического поля, а в случае волны, бегущей вдоль струны, распространяются колебания частиц струны, отклоняющихся от положения равновесия в направлении, перпендикулярном самой струне. Максимальное абсолютное отклонение колеблющейся величины от равновесного значения называется амплитудой волны.
Самая простая волна имеет синусоидальную форму. Если мы сделаем мгновенный снимок такой волны, то увидим, что у нее отклонение колеблющейся величины от среднего значения обращается в ноль в некоторых точках на пути ее распространения. Если, начав с одной из них, мы будем двигаться от нее вперед в направлении распространения волны, то увидим, как отклонение от среднего плавно увеличивается, пока не сравняется с амплитудой волны, и затем плавно опускается до нуля. Если мы последуем дальше, то увидим, что отклонение падает до отрицательного значения амплитуды и вновь возвращается к нулю, а затем весь цикл повторяется снова и снова по мере того, как мы двигаемся дальше в прежнем направлении. Расстояние между двумя соседними точками в начале и в конце полного цикла называется длиной волны и обычно обозначается символом λ (лямбда). Для восприятия дальнейшего объяснения важно понять, что, поскольку мгновенный уровень возвращается к нулю не только в начале и конце цикла, но еще и в середине, расстояние между двумя соседними нулевыми точками равняется половине длины волны, λ/2. Это значит, что любые две мгновенные точки с нулевым уровнем волны должны быть отделены друг от друга целым количеством отрезков с длиной, равной половине длины волны.
В математике есть фундаментальная теорема (впервые сформулированная только в первой половине XIX в.), которая доказывает, что практически любое возмущение (точнее, любое возмущение, достаточно гладко изменяющееся вдоль линии распространения волны) можно представить как результат сложения синусоидальных волн с разными длинами (это называется гармоническим анализом, или «фурье‑анализом»).
Каждая синусоидальная волна предполагает не только изменение некой величины в пространстве, но и ее колебания. Если волна распространяется со скоростью v , то за время t она проходит расстояние vt . Тогда мимо фиксированной точки за время t проследует vt /λ интервалов, равных длине волны. Это значит, что в любой точке за одну секунду количество циклов, в течение каждого из которых и сама колеблющаяся величина, и скорость ее изменения вновь возвращаются к исходным значениям, равно v/λ. Эта величина называется частотой колебаний, и ее принято обозначать греческой буквой ν (ню), то есть ν = v/λ. Скорость распространения возмущения колеблющейся струны равна постоянной величине, если масса и натяжение струны практически не зависит от длины волны, и амплитуда колебаний определяется только массой струны и силой ее натяжения. Поэтому для таких волн (так же как и для световых волн) частота просто обратно пропорциональна длине волны.
Теперь рассмотрим струну какого‑нибудь музыкального инструмента. Пусть ее длина равна L . Амплитуда колебаний должна равняться нулю на обоих концах струны, в точках ее крепления. Это условие ограничивает возможные длины волн синусоидальных составляющих, на которые раскладывается любое частное колебания струны. Как мы отметили, расстояние между любыми точками синусоидальной волны, где амплитуда колебания равна нулю, должно быть кратно половине длины волны. Значит, зафиксированная на обоих концах струна должна содержать целое число N таких интервалов в половину длины волны, то есть L = Nλ /2. Это означает, что в струне возможны только волны, длины которых выражаются формулой λ = 2L/N , где N = 1, 2, 3, и т. д. Соответственно, все возможные частоты можно найти по формуле[26]:
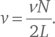
Самая низкая частота для случая, когда N = 1, равна v /2L . Все прочие частоты, соответствующие N = 2, 3, 4 и т. д., называются обертонами. Например, самая низкая частота для струны ноты до первой октавы («среднее до») – 261,63 колебаний в секунду, но еще она же вибрирует с частотой 523,26 колебаний в секунду, 784,89 колебаний в секунду и т. д. Интенсивность различных обертонов определяет качество звучания разных музыкальных инструментов.
Теперь допустим, что вибрировать заставили две струны с длинами L 1 и L 2, которые в остальном абсолютно одинаковы – в частности, скорость v распространения возмущения в обеих одинакова. За время t форма колебаний первой и второй струн на самых низких частотах для обеих пройдет через n 1 = ν 1t = vt /2L 1 и n 2 = ν 2t = vt /2L 2 циклов или частичных циклов, соответственно. Их соотношение равняется:

Таким образом, для того, чтобы частоты самого низкого из возможных для каждой из струн звуков относились как целые числа, величина L 2/L 1 должна выражаться простой целочисленной дробью, то есть рациональным числом (в этом случае и для каждого обертона частоты будут удовлетворять тому же условию). Звуки обеих струн в этом случае сольются, как если бы щипнули одну струну, а не две. По всей видимости, именно поэтому мы воспринимаем получившееся созвучие как консонанс.
Например, если L 2/L 1 = 1/2, то на каждое колебание первой струны придется два полных цикла второй. В этом случае говорят, что звуки, издаваемые первой и второй струнами, образуют интервал октаву. Все клавиши ноты до на клавиатуре фортепиано производят музыкальные звуки, каждый из которых отделен от соседнего интервалом в одну октаву. Если отношение L 2/L 1 = 2/3, то получающийся интервал называется квинтой. Например, это справедливо в случае, когда первая струна звучит на ноте до первой октавы с главной частотой 261,63 колебаний в секунду, а вторая струна, длина которой 2/3 от первой, звучит на ноте соль первой октавы с частотой 3/2 × 261,63 = 392,45 колебаний в секунду[27]. Если соотношение L 2/L 1 = 3/4, получившийся интервал называется терцией.
Другая причина того, что эти сочетания нот благозвучны, заключается в обертонах. Чтобы N 1‑й обертон струны 1 имел ровно ту же частоту, что и N 2‑й обертон струны 2, должно выполняться равенство vN 1/2L 1 = vN 2/2L 2, и таким образом:
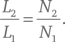
И вновь отношение длин двух струн выражается рациональным числом, хотя и по иной причине. Но если это отношение окажется равно какому‑либо нерациональному числу, например, π или квадратному корню из 2, то обертоны двух струн никогда не совпадут точно, хотя частоты более высоких обертонов могут сходиться как угодно близко. Звук, который при этом получается, ужасен.
Теорема Пифагора
Так называемая теорема Пифагора – самая знаменитая во всей планиметрии. Хотя ее доказательство приписывают ученикам и последователям Пифагора, например, Архиту Тарентскому, в точности история ее создания неизвестна. Здесь я приведу простейшее доказательство, основанное на понятии пропорциональности, широко применявшемся древнегреческими математиками.
Рассмотрим треугольник с вершинами A, B и P , у которого угол при вершине P является прямым. Теорема утверждает, что площадь квадрата, сторона которого равна AB (гипотенуза треугольника), равняется сумме площадей квадратов, стороны которых равны двум другим сторонам того же треугольника, катетам AP и BP . Говоря языком современной алгебры, рассматривая AB, AP и BP как численные величины, равные длинам указанных сторон, должно быть справедливо равенство:
AB ² = AP ² + BP ² .
Чтобы доказать теорему, следует провести перпендикуляр к гипотенузе AB из вершины P . Обозначим точку его пересечения с гипотенузой C (см. рис. 2). Таким образом мы поделим исходный треугольник ABP на два меньших прямоугольных треугольника APC и BPC . Легко видеть, что оба меньших треугольника подобны исходному прямоугольному треугольнику, то есть все углы в них те же самые, что и в большом. Если мы обозначим углы при вершинах A и B α (альфа) и β (бета), то у треугольника ABP будут углы α, β и 90°, и значит, α + β + 90° = 180°. В треугольнике APC два угла равны α и 90°, значит, третий угол равняется β. Аналогично в треугольнике BPC два угла равны β и 90°, следовательно, третий угол равен α.
Так как все три треугольника взаимно подобны, их соответствующие стороны пропорциональны. Это означает, что длина катета AC относится к длине гипотенузы AP треугольника ACP так же, как длина катета AP к длине гипотенузы AB в исходном треугольнике ABP . Соответственно, BC относится к BP в той же пропорции, что и BP к AB . Мы можем выразить это в более привычной алгебраической форме, связав длины сторон пропорцией:

Отсюда очевидно следует, что AP ² = AC × AB , а BP ² = BC × AB . Складывая два этих уравнения вместе, получаем:
AP ² + BP ² = ( AC + BC ) × AB.
Но AC + BC = AB , что и требовалось доказать.

Рис. 2. Доказательство теоремы Пифагора. Согласно теореме, сумма площадей квадратов, стороны которых равны катетам AP и BP , равняется площади квадрата, стороной которого является гипотенуза AB . Для доказательства теоремы из точки P в точку C проводится перпендикуляр к гипотенузе AB .
Дата добавления: 2016-01-29; просмотров: 741;
