Установившаяся скорость падения

Здесь g – постоянная величина, не зависящая от того, какое именно тело падает. Оно обозначает ускорение свободного падения тела в вакууме и вблизи земной поверхности, приблизительно равное 9,8 м/с за секунду. Вторая сила – сопротивление воздуха. Она выражается функцией f (v ), значение которой пропорционально плотности воздуха, увеличивается с ростом скорости и зависит от формы и размера тела, но не зависит от его массы:

F _в = −f(v) = kv.

f(v) = Kv ² ,

где K – другая положительная константа.

Подставив в формулу для полной силы, действующей на падающее тело, F = F_т + F_в выражения для сил тяготения и сопротивления и заменив затем полученной суммой множитель силы во Втором законе Ньютона, получаем:

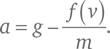
Когда тело только‑только отпустили и оно лишь начало падать, его скорость еще ничтожно мала, поэтому сила сопротивления воздуха не действует, и оно просто летит вниз с ускорением, равным g . По мере падения его скорость растет и сопротивление воздуха начинает уменьшать ускорение падения. В конце концов скорость становится такой, что слагаемое – f (v )/m сравнивается по модулю со слагаемым g в формуле выше и ускорение падает до близкой к нулю величины. Эта скорость называется установившейся скоростью падения и определяется как корень уравнения

f (v_уст) = gm.

Аристотель нигде не упоминал установившуюся скорость падения, но та скорость, которую можно определить по этой формуле, характеризуется теми же свойствами, которые он приписывал скоростям падающих тел. Поскольку f (v ) – монотонно возрастающая функция от v , то установившаяся скорость возрастает с ростом массы m . В особом случае, когда f (v ) = kv , установившаяся скорость падения прямо пропорциональна массе и обратно пропорциональна коэффициенту сопротивления:

Но в общем случае зависимость скорости падающих тел от времени может быть иной. Так или иначе, тяжелые тела приобретают присущую им установившуюся скорость только после продолжительного падения.

Падение капель

Стратон пронаблюдал, что падающие одна за другой капли одной струи отдаляются друг от друга все больше и больше по мере падения. Из этого факта он заключил, что капли падают ускоренно. Если одна капля в какой‑то момент падения оказалась ниже другой, это значит, что первая из них прошла большее расстояние. К тому же, раз капли по мере падения отдаляются, то та из них, которая падает дольше, падает быстрее, демонстрируя ускоренное падение. Хотя Стратон не знал этого, ускорение в этом случае постоянно, и, как мы увидим, результатом является то, что разрывы между каплями в цепочке капель, в которую превращается струя, возрастают пропорционально времени падения.

Как упоминалось в техническом замечании 6, если сопротивлением воздуха можно пренебречь, то ускорение падающего тела равно g , ускорению свободного падения, которое вблизи поверхности Земли равно 9,8 м/с за секунду. Если в начальный момент падения тело находилось в покое, то по истечении интервала времени τ (тау) его скорость будет равна g τ. Таким образом, если две одинаковые капли 1 и 2 срываются со среза одного и того же сливного лотка в различные моменты времени t ₁ и t ₂, то в какой‑то более поздний момент времени они приобретут скорости v ₁ = g (t – t ₁) и v ₂ = g (t – t ₂) соответственно. Разность их скоростей, таким образом, составит:

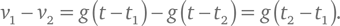
Несмотря на то что и v ₁, и v ₂ растут со временем, их разность не зависит от конкретного момента t , поэтому расстояние s между двумя каплями просто увеличивается прямо пропорционально времени:

Например, если вторая капля срывается со среза сливного лотка на одну десятую долю секунды позже первой, то половину секунды спустя две капли окажутся на расстоянии 9,8 × 1/2 × 1/10 = 0,49 м одна от другой.

Отражение

Открытие закона отражения световых лучей Героном Александрийским явилось одним из самых ранних примеров того, как закон физики выводится средствами математики из другого, более общего принципа. Допустим, наблюдатель в точке A видит отражение в зеркале объекта в точке B . Если наблюдатель видит изображение в точке P на зеркале, то световой луч в таком случае проделал путь из точки B в точку P , а затем в точку A (Герон, вероятно, сказал бы, что луч прошел от наблюдателя из точки A к зеркалу, а затем к объекту в точке B , как если бы глаз таким образом дотронулся до объекта, но на ход наших рассуждений это не повлияет). Задача заключается в следующем: где именно на зеркале находится точка P ?

Чтобы ответить на этот вопрос, Герон предположил, что свет всегда следует кратчайшим путем. В случае отражения это означает, что точка P должна быть расположена так, чтобы общая длина пути из B в P , а затем в A была бы наименьшей среди всех возможных путей из двух прямолинейных отрезков между точкой B , зеркалом и точкой A . Отсюда он заключил, что угол θ_п (тета_п ) между зеркалом и падающим на него лучом света (отрезком между точкой B и зеркалом) равен углу θ_о между зеркалом и отраженным лучом (отрезком между зеркалом и точкой A ).

Доказательство правила о равных углах падения и отражения таково. Начертим прямую, перпендикулярную поверхности зеркала, проходящую через точку B и точку B ′, которая находится на таком же расстоянии позади зеркала, как B перед ним (см. рис. 3). Допустим, что эта прямая пересекает зеркало в точке C . Катеты B ′C и CP прямоугольного треугольника B ′CP имеют ту же длину, что и катеты BC и CP в треугольнике BCP , поэтому гипотенузы B ′P и BP этих двух прямоугольных треугольников также должны быть равны. Значит, полное расстояние, которое луч света проходит из B в P , а потом в A , такое же, как если бы он проходил из B ′ в P , а затем в A . Кратчайшее расстояние между точками B ′ и A – это отрезок прямой, а значит, кратчайший путь между реальным объектом и наблюдателем – такой, при котором точка P лежит на отрезке B ′A . В случае пересечения двух прямых линий противолежащие по отношению к точке пересечения углы равны, поэтому угол θ между отрезком B ′P и зеркалом равен углу θ_о между отраженным лучом и зеркалом. Но поскольку у прямоугольных треугольников B ′CP и BCP все стороны одинаковы, угол θ должен быть также равен углу θ_п между падающим лучом и зеркалом. Таким образом, поскольку и θ_о , и θ_п равны θ, они взаимно равны. Это фундаментальное правило равенства углов падения и отражения определяет положение точки P , которая соответствует изображению объекта в зеркале.

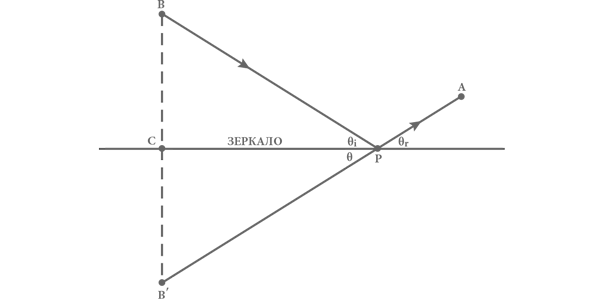
Рис. 3. Доказательство теоремы Герона. Теорема доказывает, что кратчайший путь из объекта B до поверхности зеркала и затем к наблюдателю в точке A таков, что углы θ_п и θ_о равны. Начерченные сплошной линией отрезки помечены стрелками, показывающими направление движения луча света. Штриховая линия – перпендикуляр к поверхности зеркала между точкам B и B’ , находящимися на одинаковом расстоянии от зеркала, но по разные стороны от него.