Когда Луна в фазе первой или последней четверти, угол между направлениями на Луну и на Солнце составляет 87°.

Если в этот момент смотреть с Луны, угол между направлениями на Солнце и на Землю должен составлять точно 90° (см. рис. 5а), поэтому треугольник, образованный отрезками Луна – Солнце, Луна – Земля и Земля – Солнце, является прямоугольным, в котором отрезок Земля – Солнце есть гипотенуза. Отношение катета, прилежащего к углу θ (тета) в прямоугольном треугольнике, к его гипотенузе – тригонометрическая функция косинус угла θ, которая обозначается cos θ, и ее значение мы можем взять из таблицы или рассчитать на калькуляторе с тригонометрическими функциями. Итак,

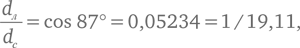
и значит, из наблюдения следует, что Солнце в 19,11 раз дальше от Земли, чем Луна. Не зная тригонометрии, Аристарх мог лишь заключить, что это число не меньше 19 и не больше 20. На самом деле этот угол равен не 87°, а 89,853°, и поэтому Солнце в действительности находится в 389,77 раз дальше от Земли, чем Луна.

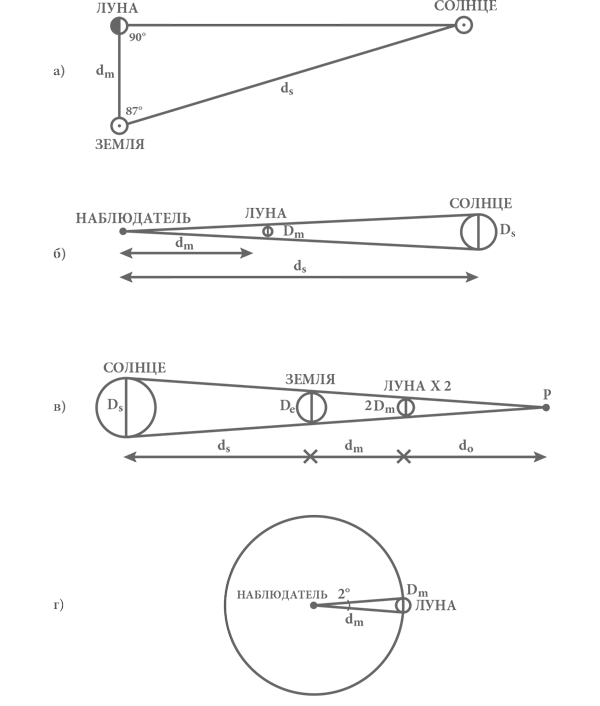
Рис. 5. Четыре наблюдения, которые Аристарх использовал для расчета размеров Солнца и Луны и расстояний от Земли до них: а) треугольник, образуемый Землей, Солнцем и Луной в момент, когда Луна находится в середине фазы первой или последней четверти; б) диск Луны точно закрывает диск Солнца для земного наблюдателя во время полного солнечного затмения; в) Луна заходит в тень Земли во время полного лунного затмения. Сфера, которая на месте Луны точно перекрывала бы конус тени, имеет диаметр, вдвое больший, чем у Луны, а точка P – крайняя точка конуса тени, отбрасываемой Землей; г) видимый угловой размер Луны по Аристарху составляет 2°; истинное его значение близко к 0,5°.

Наблюдение 2