Луна имеет угловой размер 2°.

Поскольку угловой размер дуги полной окружности равен 360° (см. рис. 5 г) и длина окружности радиусом dл равна 2πdл , то диаметр Луны равен

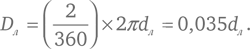
По Аристарху, значение отношения D_л /d_л лежит в промежутке между 2/45 = 0,044 и 1/30 = 0,033. По неизвестным причинам в сохранившихся трудах Аристарх грубо ошибается в своей оценке видимого углового диаметра Луны. На самом деле он составляет 0,519°, что сводит значение D_л /d_л к 0,0090. Как мы отметили в главе 8, Архимед в своем труде «Исчисление песчинок» дает величину для углового диаметра Луны 0,5°, что довольно близко к истинному значению и могло бы дать правильные оценки диаметра Луны и расстояния до нее.

Используя результаты наблюдений 2 и 3, из которых Аристарх получил отношение D_з /D_л диаметров Земли и Луны, и свой результат наблюдения 4, давший ему отношение D_л /d_л диаметра Луны к расстоянию до нее, он смог найти отношение расстояния до Луны к диаметру Земли. Например, полагая D_з /D_л = 2,85 и D_л /d_л = 0,035, получаем:

(Истинное значение – около 30.) Далее, совмещая эту величину с результатом наблюдения 1, дающим отношение расстояния от Земли до Солнца и до Луны как d_с /d_л = 19,1, Аристарх нашел, что расстояние от Земли до Солнца в d_с /D_з = 19,1 × 10,0 = 191 раз больше диаметра Земли, тогда как в действительности оно в 11 600 раз больше. Осталось измерить Землю, но это уже следующая задача.

Размер Земли

Для его расчета Эратосфен воспользовался сведениями о том, что в полдень во время летнего солнцестояния в Александрии направление на Солнце составляет 1/50 часть полной дуги окружности (то есть 360°/5 = 7,2°) от направления в зенит, тогда как в то же время в Сиене – городе, который, как он предполагал, лежит точно к югу от Александрии – в тот же самый полдень солнце было точно в зените. Поскольку Солнце расположено очень далеко, его лучи, падающие на поверхность Земли в Александрии и Сиене, можно считать параллельными. Вертикаль, то есть направление в зенит для любого города на поверхности Земли, – это продолжение луча, проведенного из центра земного шара к точке расположения этого города на его поверхности, поэтому угол между лучами от центра Земли к Сиене и Александрии должен также составлять 7,2°, или 1/50 часть полной дуги (см. рис. 6). А значит, если основываться на предположениях Эратосфена, длина окружности земного шара должна быть в 50 раз длиннее расстояния от Александрии до Сиены.

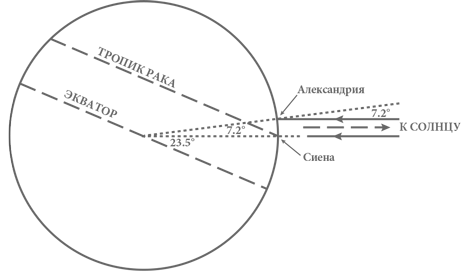
Рис. 6. Схема наблюдения Эратосфена, которую он использовал для определения размера Земли. Горизонтальные линии со стрелками демонстрируют направление падения солнечных лучей во время летнего солнцестояния. Пунктирные линии представляют собой лучи, проведенные из центра Земли к Александрии и Сиене, и соответствуют перпендикулярам к поверхности Земли.

Сиена находится не на экваторе Земли, как можно подумать, бегло глядя на рисунок, а близко к Северному тропику, или тропику Рака – широте, расположенной на 23,5 к северу от экватора (иначе говоря, угол между направлениями из центра Земли на какую‑либо точку на тропике Рака и точку на экваторе точно к югу от нее составляет 23,5°). Во время летнего солнцестояния солнце в полдень стоит в небе прямо над головой на тропике Рака, а не на экваторе, потому что ось вращения Земли не перпендикулярна плоскости ее орбиты, а отклонена от перпендикуляра на угол 23½°.

Эпициклы внутренних и внешних планет

В своем «Альмагесте» Птолемей представил теорию движения планет, согласно которой, в ее простейшем виде, каждая планета движется по окружности, называемой эпициклом, вокруг точки в пространстве, которая сама обращается вокруг Земли по окружности, которая называется деферент. Здесь мы ответим на вопрос, почему эта теория работала так хорошо, предсказывая видимые движения планет. Ответ на него оказывается различным для случая внутренних планет (Меркурия и Венеры) и внешних планет (Марса, Юпитера и Сатурна).

Сначала рассмотрим внутренние планеты – Меркурий и Венеру. По современным представлениям, и Земля, и эти планеты обращаются вокруг Солнца на приблизительно постоянном расстоянии от него и примерно с неизменной скоростью. Если мы не станем принимать во внимание законы физики, мы можем считать, что в центре находится Земля. Тогда Солнце будет обращаться вокруг нее, а все остальные планеты будут обращаться вокруг Солнца на постоянных расстояниях и с постоянными скоростями. Это представление соответствует простейшему варианту теории, позднее предложенной Тихо Браге, сторонником которой, возможно, был и Гераклид. Она дает верные предсказания положений планет, не считая небольших поправок, необходимых потому, что планеты на самом деле движутся по эллиптическим орбитам, близким к круговым, а не в точности по окружностям, и Солнце расположено не в центрах этих эллипсов, а на некотором расстоянии от центров, к тому же и скорость планеты слегка изменяется по мере ее движения по орбите. Описанная система является особым случаем планетной теории Птолемея, хотя сам Птолемей такой случай никогда не рассматривал: в нем деферентом является не что иное, как орбита Солнца вокруг Земли, а эпициклом – орбита Меркурия или Венеры вокруг Солнца.

Заботясь лишь о расчете видимых положений Солнца и планет, переменное расстояние любой планеты от Земли можно умножать на произвольную константу, получая тот же самый результат. Так получится, например, если радиус и эпицикла, и деферента планеты помножить на одно и то же число, которое для Меркурия и Венеры может быть произвольно различным. Допустим, мы примем, что радиус деферента Венеры равен половине расстояния от Земли до Солнца, а радиус ее эпицикла – половине радиуса орбиты Венеры вокруг Солнца. Это не скажется на том факте, что центры эпициклов планет все время будут располагаться на прямой, проходящей через Землю и Солнце (см. рис. 7а, на котором схематично, не в истинном масштабе, изображен пример эпицикла и деферента внутренней планеты). Эта трансформация не скажется на видимом движении Венеры и Меркурия по небу до тех пор, пока мы не поменяем соотношение радиусов эпицикла и деферента каждой из планет. Такова упрощенная версия теории, предложенной Птолемеем для описания движений внутренних планет. Согласно ей, один оборот планеты по эпициклу занимает столько же времени, сколько ей в реальности необходимо для оборота вокруг Солнца: 88 суток для Меркурия и 225 суток для Венеры. При этом центр эпицикла, как и Солнце, обращается вокруг Земли, и один его полный оборот занимает промежуток времени, равный земному году.

Предметно говоря, притом что мы не меняем отношения радиусов эпицикла и деферента, должно быть справедливо равенство

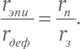
Здесь r_эпи и r_деф – радиусы эпицикла и деферента в системе Птолемея, а r_п и r_з – радиусы орбит той же планеты и Земли в системе Коперника (или, что то же самое, радиус орбит планеты вокруг Солнца и Солнца вокруг Земли, соответственно, в теории Тихо Браге). Конечно, Птолемей ничего не знал о системах Тихо Браге или Коперника, и свою теорию он разрабатывал иным путем. Все сказанное по этому поводу выше лишь показывает, почему теория Птолемея работала, а не то, каким образом он вывел ее.

Теперь обратимся к внешним планетам – Марсу, Юпитеру и Сатурну. В простейшей версии теории Коперника (как и у Тихо Браге) каждая из этих планет постоянно находится на одном и том же расстоянии не только от Солнца, но и от точки C’ , движущейся в пространстве, сохраняя одно и то же расстояние от Земли. Чтобы найти эту точку, начертим параллелограмм (рис. 7б), первые три вершины которого в порядке против часовой стрелки будут таковы: S – точка расположения Солнца, E – точка расположения Земли, P’ – точка расположения одной из планет. Движущаяся точка C’ находится в четвертом, пустом углу этого параллелограмма.

Рис. 7. Упрощенная версия теории эпициклов, описанной Птолемеем: а) схема, согласно Птолемею, изображающая движение одной из внутренних планет – Меркурия или Венеры; б) схема движения одной из внешних планет – Марса, Юпитера или Сатурна – согласно теории Птолемея. Планета P обращается по эпициклу вокруг точки C за один год, при этом отрезок CP всегда параллелен отрезку, соединяющему Землю и Солнце, в то время как сама точка C обращается вокруг Земли по деференту за более длительное время (штриховые линии отражают особый случай теории Птолемея, в котором она эквивалентна теории Коперника).

Поскольку отрезок ES имеет фиксированную длину, а отрезок P’C’ является противоположной ему стороной параллелограмма, то P’C’ также имеет фиксированную длину, равную длине первого отрезка. Поэтому планета все время остается на одном и том же расстоянии от C’ , равном расстоянию от Земли до Солнца. Это особый случай теории Птолемея, не рассмотренный им самим. В нем деферент – не что иное, как орбита точки C’ вокруг Земли, а эпицикл – орбита Марса, Юпитера или Сатурна вокруг точки С’ .

И вновь, если думать лишь о расчете видимых положений Солнца и планет, можно умножить переменное расстояние любой планеты от Земли на произвольную константу, не меняя видимую картину, и этого можно достигнуть, перемножая радиусы эпицикла и деферента каждой планеты на одну и ту же постоянную величину, индивидуальную для каждой внешней планеты. И хотя у нас больше не получается параллелограмм, отрезок от планеты до точки C остается параллельным отрезку между Солнцем и Землей. Видимое движение любой из внешних планет по небу не изменится в результате такой трансформации, если неизменным останется соотношение радиусов ее деферента и эпицикла. Такова упрощенная версия теории Птолемея, предложенной им для описания движения внешних планет. Согласно ей, один оборот по эпициклу вокруг точки C планета совершает за год, в то время как точка C обращается по деференту вокруг Земли за то время, которое по‑настоящему требуется планете, чтобы совершить оборот по орбите вокруг Солнца: 1,9 земных лет для Марса, 12 лет для Юпитера, 29 лет для Сатурна.

При неизменности отношения радиусов деферента и эпицикла должно быть справедливо равенство

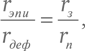
где r_эпи и r_деф снова обозначают радиусы эпицикла и деферента в системе Птолемея, а r_п и r_з – радиусы орбит планеты и Земли, соответственно, в системе Коперника (или, аналогично, радиус орбиты планеты вокруг Солнца и радиус орбиты Солнца вокруг Земли в системе Тихо Браге). Опять же, здесь мы не описали то, каким образом Птолемей пришел к формулировкам своей теории, а лишь пояснили причину того, почему она работала довольно хорошо.

Параллакс Луны

Обозначим угол между направлением в зенит и на Луну, видимую из некоторой точки O земной поверхности, как ζ’ (дзета штрих). Луна непрерывно и равномерно движется вокруг центра Земли, поэтому, анализируя серию повторяющихся наблюдений Луны, можно вычислить направление от центра Земли C к центру Луны M . В частности, можно рассчитать угол ζ между лучом, на котором находится отрезок CM , и лучом из центра Земли C , пересекающим поверхность Земли в точке O , который совпадает с направлением в зенит в этой точке. Углы ζ и ζ’ слегка отличаются, потому что радиус Земли r_з , хотя и мал по сравнению с расстоянием между центром Земли и Луной d , но не пренебрежимо мал. Именно из разности этих углов Птолемей смог вывести отношение d /r_з .

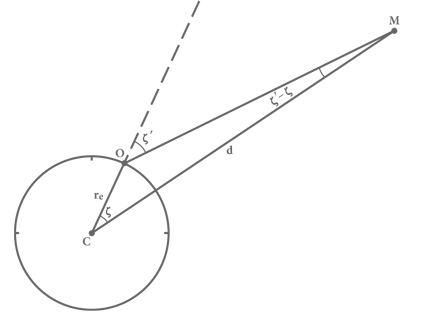
Рис. 8. Использование параллакса для определения расстояния до Луны. Здесь ζ’ – угол между наблюдаемым положением Луны и вертикалью, а ζ – то значение, которое было бы у этого угла, если можно было наблюдать Луну из центра Земли.

Точки C, O и M образуют треугольник, в котором угол при вершине C равен ζ, угол при вершине O равен 180° – ζ’, а при вершине M , поскольку сумма углов любого треугольника равна 180°, угол будет 180° − ζ – (180° − ζ’) = ζ’ − ζ (см. рис. 8). Отношение d /r_з из значений этих углов мы можем получить намного проще, чем это делал Птолемей, воспользовавшись теоремой из современной тригонометрии: в любом треугольнике длина каждой стороны пропорциональна синусу противолежащего угла (о том, что такое синус, расскажем в техническом замечании 15). Угол, противолежащий отрезку CO длиной r_з , равен ζ’ − ζ, а угол, противолежащий отрезку CM длиной d , равен 180° − ζ, поэтому

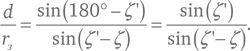
1 октября 135 г. Птолемей определил, что зенитный угол при наблюдении из Александрии составляет ζ’ = 50°55’, и его расчеты показали, что в тот же самый момент при наблюдении из центра Земли угол ζ был бы равен 49°48’. Соответствующие синусы этих углов равны

Зная эти числа, Птолемей смог заключить, что расстояние от центра Земли до Луны в единицах радиуса Земли составляет:

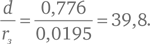
Эта величина существенно меньше, чем настоящее значение, в среднем примерно равное 60. Проблема оказалась в том, что Птолемей неточно определил разность углов ζ’ и ζ, но по крайней мере полученный результат давал верное представление о том, какого порядка величина расстояния до Луны.

Так или иначе, Птолемей рассчитал его более точно, чем Аристарх, который на основании своих расчетов отношения диаметров Земли и Луны, а также расстояния до Луны к ее диаметру смог бы указать предельные значения для d /r_з , равные 215/9 = 23,9 и 57/4 = 14,3. Однако если бы Аристарх использовал правильное значение 1/2° для углового диаметра лунного диска вместо неверной величины 2°, то соотношение d /r_з у него получилось бы в 4 раза больше, в промежутке от 57,2 до 95,6. Такой промежуток включал бы истинную величину.