Пересечение поверхности и плоскости

Линия пересечения поверхности с плоскостью представляет собой линию, называемую сечением. Точки этой кривой можно рассматривать как точки пересечения линий поверхности с плоскостью или прямых плоскости с поверхностью.

Отсюда следуют два варианта построения сечения:

1) выбираем конечное число линий на поверхности и определяем точки пересечения их с плоскостью;

2) выделяем конечное число прямых на плоскости и строим точки пересечения их с поверхностью.

Заметим, что возможно решение, представляющее собой комбинацию этих вариантов. В любом случае построение сечения сводится к многократному применению алгоритма решения задачи на пересечение линии и поверхности.

Построение сечения существенно упрощается, если плоскость занимает проецирующее положение. Это связано с тем, что проецирующая плоскость характеризуется собирательным свойством. В этом случае одна из проекций сечения находится на следе плоскости, т.е. известна.

В пересечении гранных поверхностей плоскостями получаются многоугольники (рис. 49 а). Их вершины определяются как точки пересечения ребер гранных поверхностей с секущей плоскостью. Секущая плоскость Σ является фронтально-проецирующей, следовательно, все линии, лежащие в этой плоскости, совпадут с фронтальным следом Σ₂ плоскости Σ. Следовательно, фронтальная проекция 1₂2₂3₂ сечения определится при пересечении фронтальных проекций ребер пирамиды со следом Σ(Σ₂). Горизонтальные проекции точек 1(1₁), 2(2₁) и 3(3₁) находим из условия принадлежности точек ребрам пирамиды.

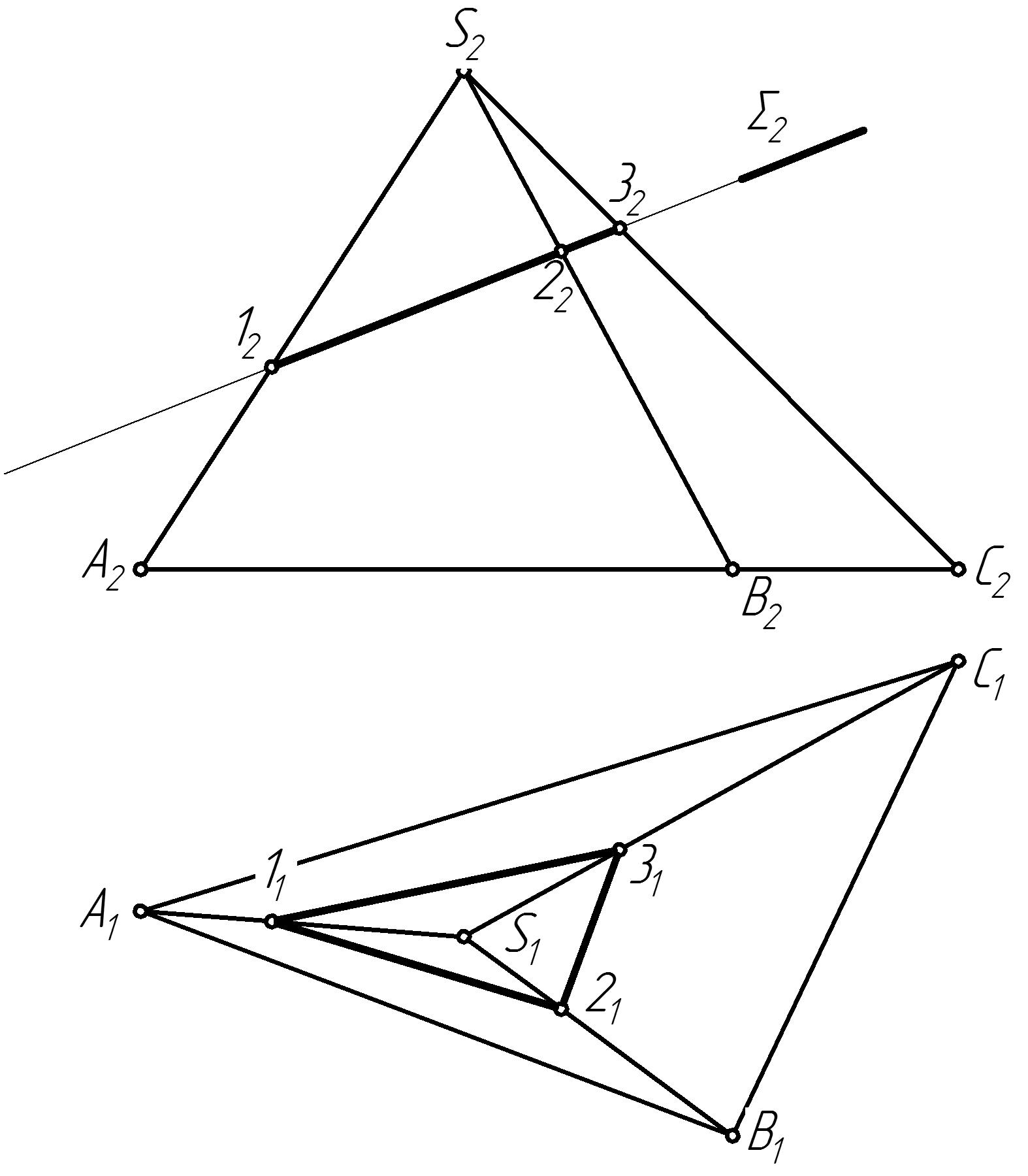
а б

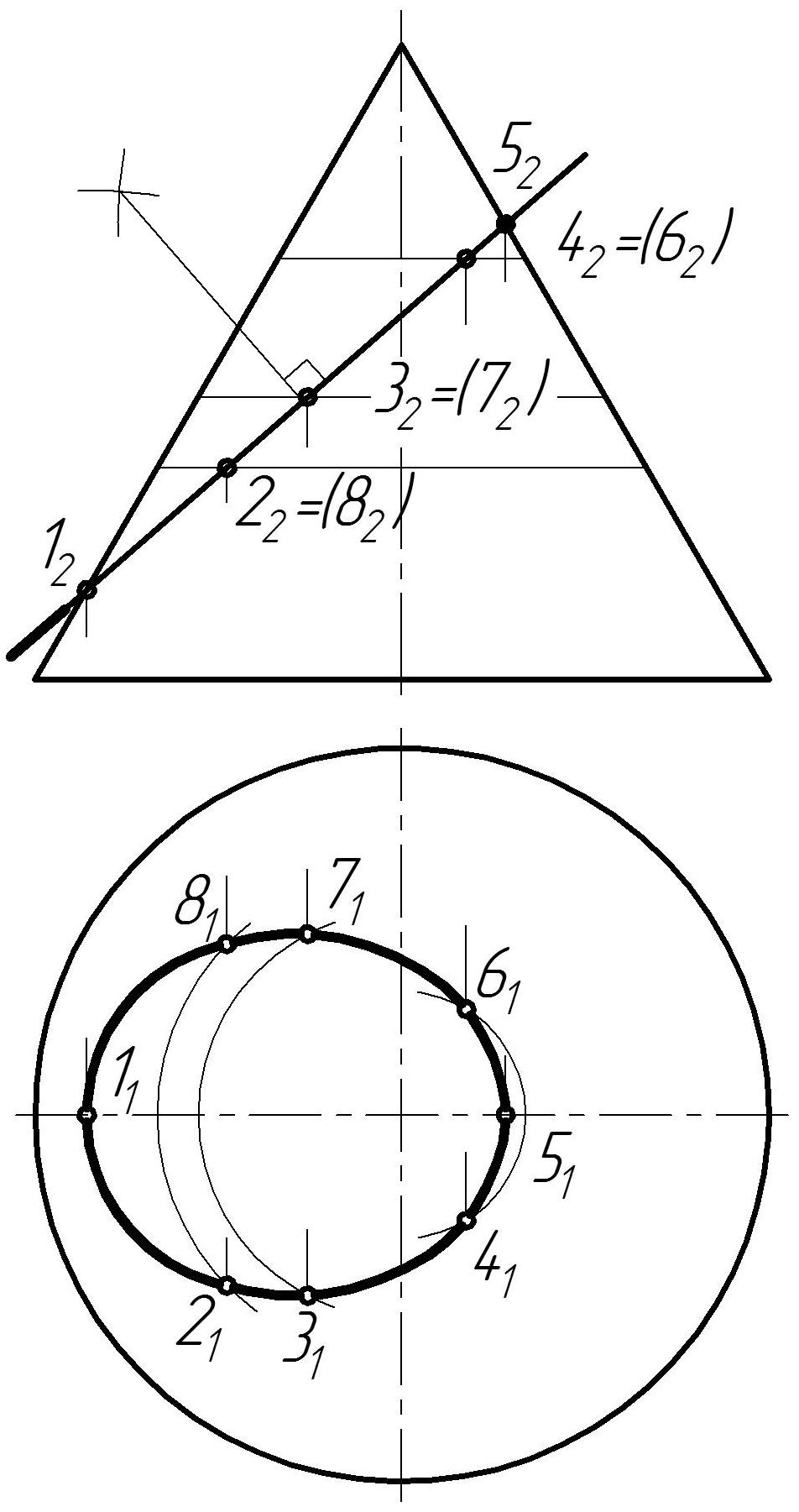
Рис. 49 Построение линии пересечения поверхности с плоскостью

Построение линии пересечения конической поверхности вращения с фронтально-проецирующей плоскостью Σ показано на рис. 49 б. Заданная плоскость Σ пересекает исходную поверхность по эллипсу, фронтальная проекция которого расположена на следе этой плоскости. Горизонтальную проекцию сечения строим по точкам из условия их принадлежности поверхности конуса (см. рис. 49 б).

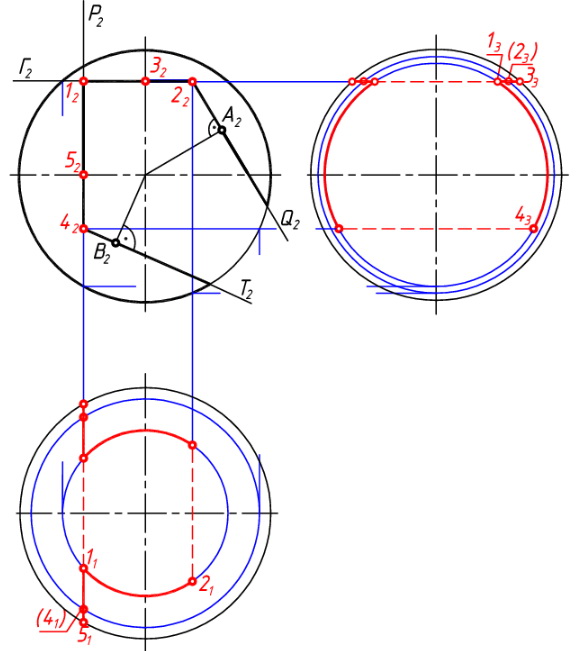
Рассмотрим построение выреза сферы, образованного с помощью четырех проецирующих секущих плоскостей (рис.51, а )[1]. Каждая из них пересекает сферу по линии, являющейся частью окружности. Кроме того, Г и Р являются горизонтальной и профильной плоскостями уровня соответственно. Проекции выреза на П₁ и П₃ будут симметричными.

а	б
в	г

На плоскостях проекций П₁ и П₃ ветви выреза от плоскостей Q и Т будут проецироваться в виде частей эллипсов. Точки А и В являются концами осей этих эллипсов.

Отметим опорные точки в плоскостях уровня: 1, 2 и 4 конечные точки ветвей выреза; 5 и 3 точки перемены видимости на плоскостях П₁ и П₃ соответственно.

Построим проекции опорных точек частей выреза от секущих плоскостей Г и Р на плоскостях проекций П₁ и П₃ (рис. 51, б).

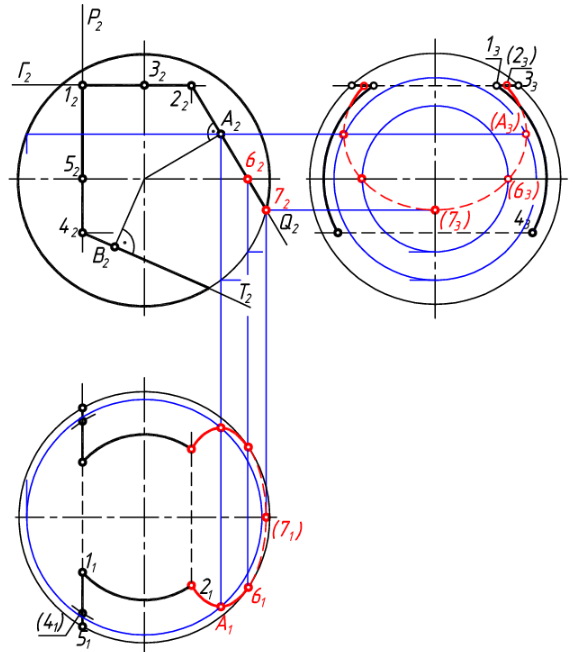
Построим ветвь выреза от плоскости Q. Опорные точки 6 перемена видимости на П₁. Опорная точка 7 низшая точка (рис. 51, в).

Построим ветвь выреза от плоскости Т. Опорные точки 8 перемена видимости на П₃. Опорная точка 9 низшая точка (рис. 51, г).

Очерки сферы и видимость линии выреза на плоскостях П₁ и П₃ определяются с учетом сквозного выреза.