Поверхности вращения
Если перемещение образующей линии представляет собой вращение вокруг некоторой неподвижной прямой (оси), то образованная в этом случае поверхность называется поверхностью вращения.
Образующая линия может быть плоской или пространственной кривой, а также прямой. Каждая точка образующей линии при вращении вокруг оси описывает окружность, которая располагается в плоскости перпендикулярной оси вращения (рис. 42).
Эти окружности называются параллелями. Следовательно, плоскости, перпендикулярные оси, пересекают поверхность вращения по параллелям. Линия пересечения поверхности вращения плоскостью Σ, проходящей через ось, называется меридианом.
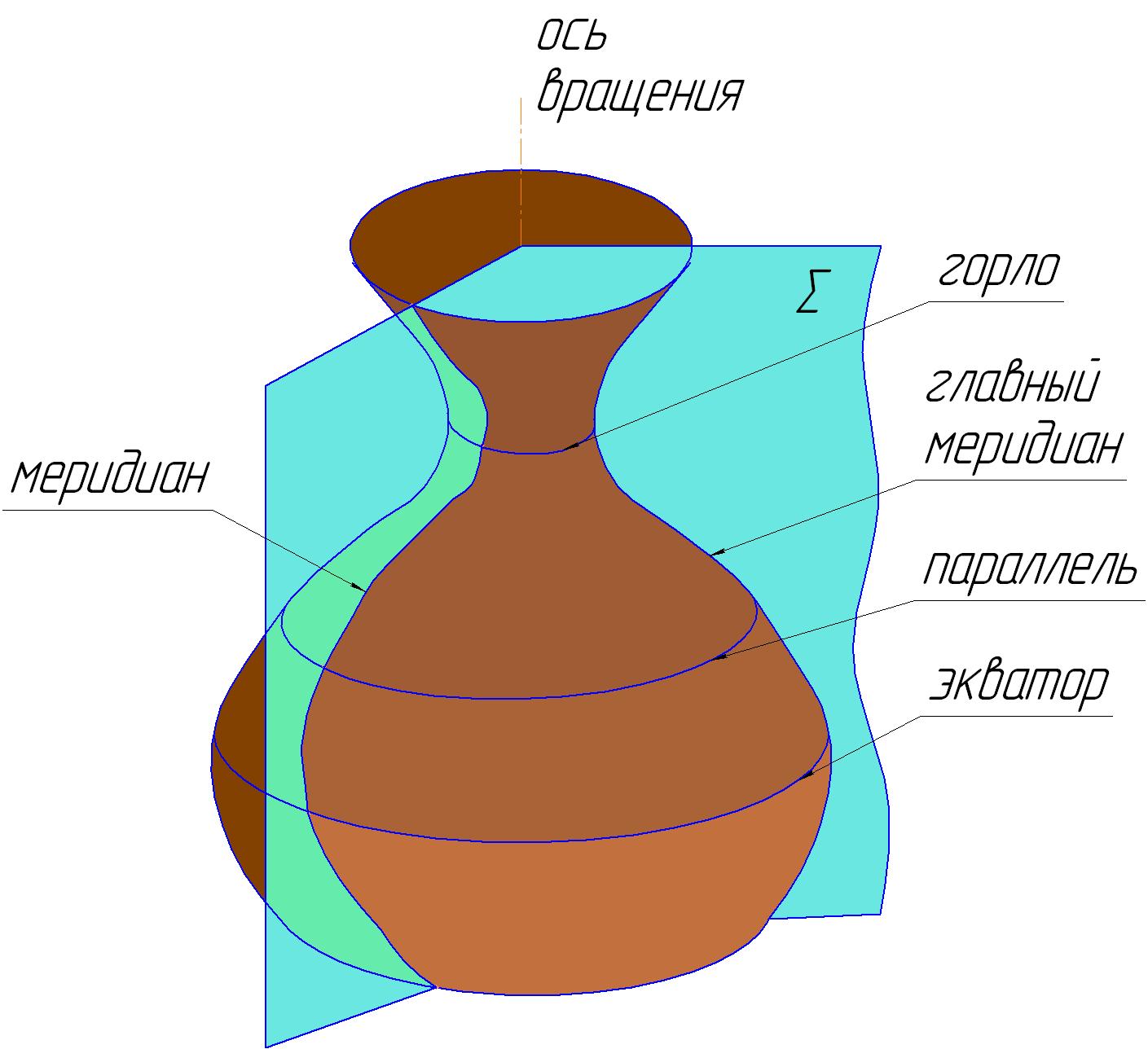 Меридиан, который является результатом пересечения поверхности вращения с плоскостью уровня, называется главным. Проекция главного меридиана на плоскость, которой параллельна плоскость уровня, является очерковой линией соответствующей проекции поверхности вращения.
Меридиан, который является результатом пересечения поверхности вращения с плоскостью уровня, называется главным. Проекция главного меридиана на плоскость, которой параллельна плоскость уровня, является очерковой линией соответствующей проекции поверхности вращения.
| Рис. 42 Элементы поверхности вращения |
При проектировании различных инженерных сооружений, машин и механизмов наибольшее распространение получили поверхности, образующиеся вращением прямой линии и кривых второго порядка.
Вращением прямой линии образуются:
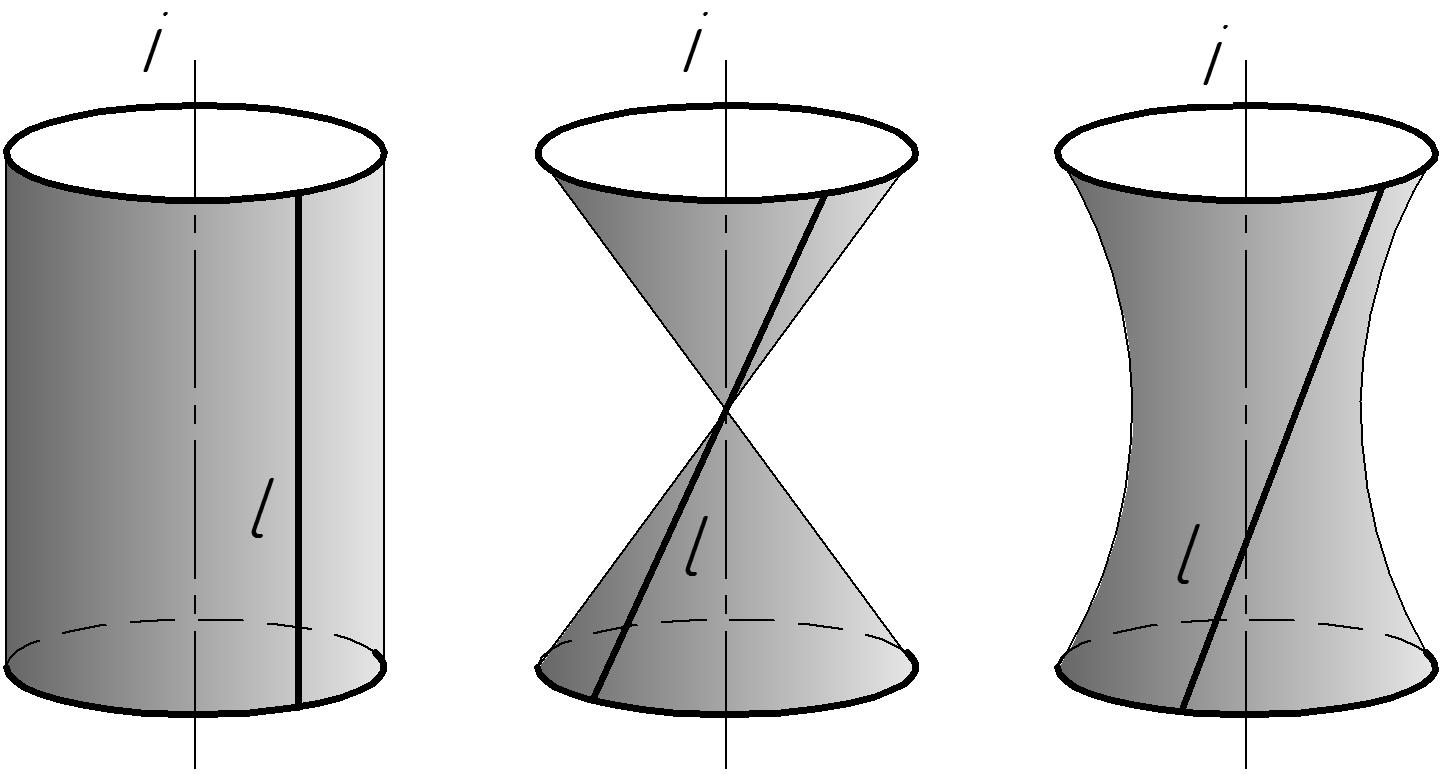
–цилиндр вращения, если прямая l параллельна оси i (рис. 43 а);
– конус вращения, если прямая l пересекает ось i (рис. 43 б);
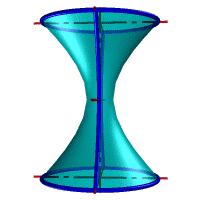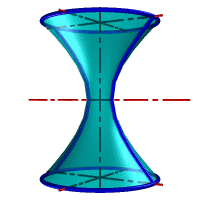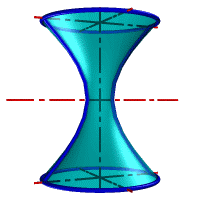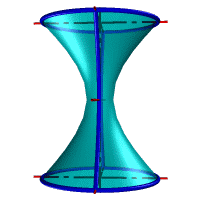
– однополостный гиперболоид, если прямая l скрещивается с осью i (рис. 43 в).
| ||
| а | б | в |
| Рис. 43 Линейчатые поверхности вращения | ||
К поверхностям вращения, образованным вращением кривых второго порядка вокруг оси относятся:
– сфера образуется вращением окружности вокруг ее диаметра (рис. 44 а);
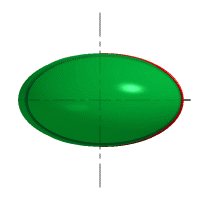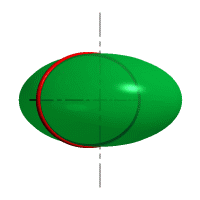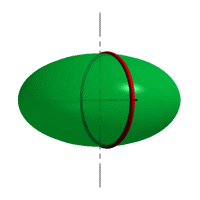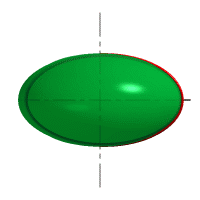
– эллипсоид вращения образуется вращением эллипса вокруг большой или малой оси (44 б, в);
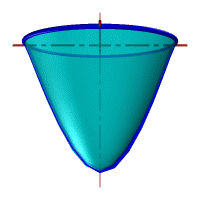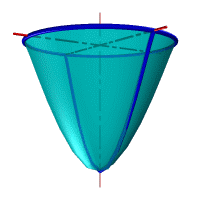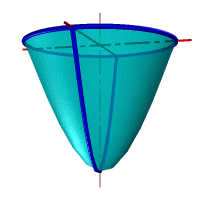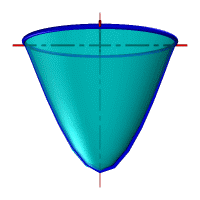
– тор образуется вращением окружности вокруг внешней оси (рис. 44 г);

| 
| 
|
| а | б | в |

| 
| 
|
| г | д | е |
| Рис. 44 Поверхности вращения второго порядка |
– однополостный гиперболоид вращения образуется вращением гиперболы вокруг ее мнимой оси. Эта поверхность образуется также вращением прямой (рис. 44 е).
Дата добавления: 2016-01-29; просмотров: 1288;
