Собственные колебания

Собственные колебания возникнут при P=0, R*=0. В таком случае уравнение колебаний примет вид

.

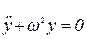Его общее решение будет:

y=A sinw t + B cosw t .

Если сделать замены A=a cosj, B=a sinj , получим

y=a sin(w t+j).

Таким образом, собственные колебания являются гармоническими.

Определим их начальную фазу φ и амплитуду a. Пусть при t=0 известны начальное отклонение y₀ и начальная скорость v₀. Тогда

y₀ =a sin φ, v₀ = 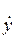(0) = aω cos φ.

Из них имеем 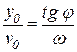и .

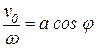Поэтому

, .

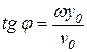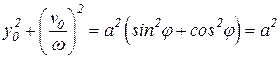Следовательно,

, .

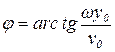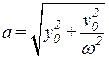Если вес массы равен G, а ускорение свободного падения g, то G=mg. К тому же, вес G вызывает статический прогиб, определяемый по формуле y_ст=G×d. Поэтому имеем

.

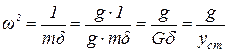Эти формулы позволяют найти частоту из решения статической задачи.

Из полученных формул вытекают следующие выводы:

1) начальная фаза и амплитуда зависят от начальных условий;

2) частота и период собственных колебаний системы не зависят от начальных условий;

3) при увеличении жесткости системы частота собственных колебаний возрастает, а при увеличении массы – уменьшается.

В о п р о с ы

1. Какие основные задачи решает динамика сооружений?

2. Чем отличается динамическая степень свободы от статической?

3. На какие три вида делятся колебания колебательных систем?

4. Какая разница между собственными и свободными колебаниями?

5. Как изменяется частота колебаний при изменении массы?

Л е к ц и я 17