Колебания систем с одной степенью свободы
Изучим колебания невесомой балки (рис. 16.7 а) с точечной массой m под действием динамической нагрузки 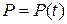 . При учете только изгибных деформаций такую балку можно рассматривать как колебательную систему с одной динамической степенью свободы.
. При учете только изгибных деформаций такую балку можно рассматривать как колебательную систему с одной динамической степенью свободы.
Уравнение колебаний массы определяется из условия динамического равновесия сил, действующих на нее (рис. 16.7 б):
J + R + R* – P = 0 ,
где 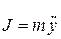 – инерционная сила; R – сила упругости балки; R* – сила сопротивления среды движению массы. Так как при колебаниях система находится в движении, это уравнение называется уравнением движения.
– инерционная сила; R – сила упругости балки; R* – сила сопротивления среды движению массы. Так как при колебаниях система находится в движении, это уравнение называется уравнением движения.
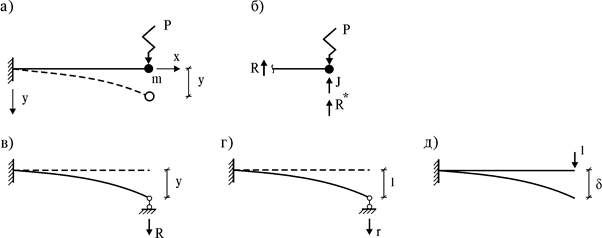
Рис. 16.7
Силу упругости R можно определить двумя способами.
Вначале воспользуемся методом перемещений. Для этого в правом конце балки введем опору и дадим ей перемещение y, возникающее при колебании массы (рис. 16.7 в). Тогда реакция во введенной связи будет равна искомой силе упругости R. Для ее определения рассмотрим единичное состояние системы: введенной опоре дадим смещение y=1 (рис. 16.7 г) и вычислим реакцию (жесткость) r. В данном случае ее можно определить по таблице метода перемещений. Так как балка упругая, то R=ry. Если эту реакцию и силу инерции подставить в предыдущее уравнение, получим уравнение вынужденных колебаний системы с одной степенью свободы в форме метода перемещений:
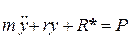 .
.
Во втором случае к концу балки приложим единичную силу. Она вызовет перемещение d (рис. 16.7 д), называемое податливостью. По теореме Бетти 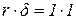 . Значит, r=1/d. Если подставить его в наше уравнение, затем поделить уравнение на m и ввести обозначение
. Значит, r=1/d. Если подставить его в наше уравнение, затем поделить уравнение на m и ввести обозначение 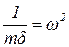 , получим уравнение колебаний системы с одной степенью свободы в форме метода сил:
, получим уравнение колебаний системы с одной степенью свободы в форме метода сил:
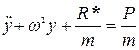 .
.
Дата добавления: 2016-01-29; просмотров: 1471;
