Удар точки о неподвижную поверхность
18.2.1 Прямой удар.
Удар называется прямым, если скорость точки до удара направлена по нормали к поверхности, скорость точки после удара также направлено по нормали.
Для оценки ударных свойств поверхности служит коэффициент восстановления.
Коэффициентом восстановления называется отношение модулей скоростей после и до удара:
.
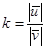Частные случаи:
; 
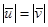- это абсолютно упругий удар;
; 
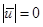- это абсолютно неупругий удар; если поверхность движется, то точка после удара движется вместе с поверхностью;
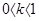- это частично упругий удар (упругий удар).
Процесс удара разделяется на две фазы:
1 - Фаза деформации продолжительностью τ1 от начала удара до момента максимальной деформации тела, принимаемого за материальную точку, в конце фазы скорость точки равна нулю.
2 - Фаза восстановления продолжительностью τ2 от момента максимальной деформации тела до отделения точки от поверхности.
Общее время удара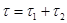 
.
При абсолютно упругом ударе форма восстанавливается полностью; при упругом - частично; при абсолютно неупругом ударе форма не восстанавливается,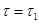 
, - удар состоит из одной фазы.
Со стороны поверхности в первой и второй фазах на тело действует ударный импульс реакции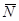 
:
; 
.
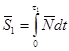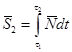По теореме об изменении количества движения при ударе:
.
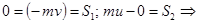
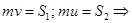
Это выражение для коэффициента восстановления k при прямом ударе через ударные импульсы S2 и S1 за вторую и первую фазы удара. Выражение справедливо и для движущейся поверхности.
Полный ударный импульс за время удара:
.
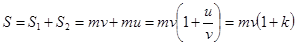При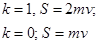 
Косой удар
Удар называется косым, если скорость точки перед ударом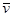 
образует с нормалью к поверхности угол 
.
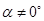α - угол падения;
β - угол отражения.
;
;
,
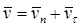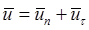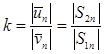где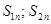 
- проекции ударных импульсов на нормаль в первой и второй фазах удара.
Если поверхность шероховатая, то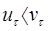 
. Примем, что поверхность не обладает ударным трением, то есть 
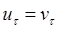, тогда
, т. к. 
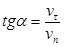, то
.
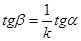Дата добавления: 2016-01-29; просмотров: 1070;