Уравнения Лагранжа (второго рода)

Уравнения Лагранжа - это дифференциальные уравнения движения системы в обобщенных координатах, имеющие следующий вид:

;

;

.........................................

,

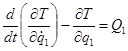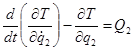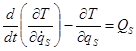где 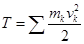- кинетическая энергия системы.

Преимущества уравнений Лагранжа:

– дают единый метод решения задач динамики;

– число уравнений Лагранжа определяется только числом степеней свободы системы и не зависит от числа точек системы и характера их движения;

– при идеальных связях в правые части входят обобщенные активные силы, то есть из рассмотрения исключены реакции связей.

Алгоритм составления уравнений Лагранжа:

– установить число степеней свободы системы;

– выбрать обобщенные координаты;

– изобразить систему в произвольном положении и приложить все активные силы, включая силу трения;

– определить обобщенные силы;

– определить кинетическую энергию систему в ее абсолютном движении;

– выразить кинетическую энергию через обобщенные координаты 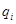и обобщенные скорости ;

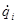– определить частные производные 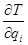и и 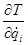подставить их в уравнения Лагранжа;

– если заданы действующие силы и начальные условия, то, интегрируя уравнения, находим закон движения системы в виде:

– ;

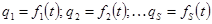– если задан закон движения, то определяем действующие силы.

Теория удара. Основные понятия и теоремы

Основные понятия.

Ударом называется явление, при котором за ничтожно малый промежуток времени скорости точек тела изменяются на конечную величину.

Ударными силами называются силы, под действием которых происходит удар.

Временем удара называется промежуток времени, в течение которого происходит удар.

Ударный импульс равен:

.

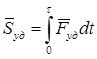Графически 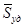изображается заштрихованной площадью под кривой .

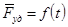Средняя ударная сила равна:

.

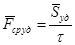Так как τ мало, то 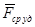велико, поэтому 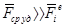, а 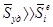. Поэтому импульсами неударных сил пренебрегают.

Так как τ мало, то считают, что за время удара точки тела не успевают изменить своего положения, поэтому перемещениями точек тел за время удара пренебрегают.

18.1.2 Основные теоремы теории удара:

Теорема об изменении количества движения точки при ударе: Изменение количества движения точки за время удара равно ударному импульсу, приложенному к точке.

,

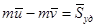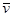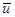где и - скорости точки до и после удара.

Теорема об изменении количества движения системы при ударе: Изменение количества движения системы за время удара равно векторной сумме внешних ударных импульсов, приложенных к точкам системы.

.

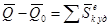Следствие: Если 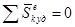, то 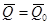, то есть количество движения системы не изменяется, если сумма внешних ударных импульсов равна нулю.

Теорема о движении центра масс системы:

.

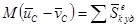Следствие: Если 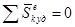, то 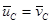, то есть скорость центра масс системы не изменится, если сумма внешних ударных импульсов равна нулю.

Теорема Кельвина (для точки): Работа силы, приложенной к точке за какой-либо промежуток времени равна скалярному произведению импульса силы за тот же промежуток времени на полусумму начальной и конечной скоростей.

.

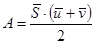Теорема Кельвина для системы:

.

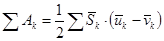Теорема об изменении кинетического момента системы при ударе: Изменение кинетического момента системы относительно точки за время удара равно векторной сумме моментов относительно той же точки внешних ударных импульсов приложенных к точкам системы.

.

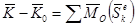В проекциях на координатные оси:

;

;

.

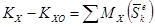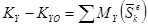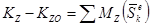Следствия:

Если удар испытывает твердое тело, вращающееся вокруг оси, то, так как ; ,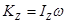

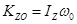Для твердого тела .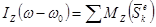

Если 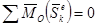, то 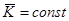- это закон сохранения кинетического момента при ударе.