Обобщенные скорости
В качестве обобщенных координат можно выбрать величины, имеющие любой геометрический смысл и размерность: отрезки прямых, дуг; углы; площади; объемы и т.д.
Система, имеющая s степеней свободы, будет иметь s обобщенных координат:
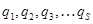 .
.
Так как эти координаты независимы, то независимы и их приращения:
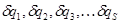 .
.
При движении системы ее независимые координаты изменяются со временем. Возьмем от них производные по времени - это обобщенные скоростисистемы:
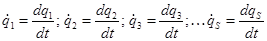 .
.
Размерность обобщенных скоростей определяется размерностью соответствующих обобщенных координат:
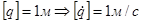 - линейная скорость;
- линейная скорость;
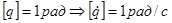 - угловая скорость;
- угловая скорость;
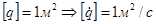 - секторная скорость.
- секторная скорость.
Понятие обобщенной скорости охватывает все виды скоростей.
Обобщенные силы
Пусть на систему, состоящую из n материальных точек, имеющую s степеней свободы действуют силы 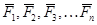 . Ее положение определяется s обобщенными координатами
. Ее положение определяется s обобщенными координатами 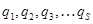 . Сообщим системе такое возможное перемещение, при котором только i-я координата получит перемещение
. Сообщим системе такое возможное перемещение, при котором только i-я координата получит перемещение 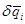 , а остальные координаты не изменятся. Сумма работ всех действующих на этом перемещении сил равна:
, а остальные координаты не изменятся. Сумма работ всех действующих на этом перемещении сил равна:
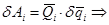
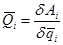 ,
,
где 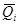 - обобщенная сила соответствующая обобщенной координате
- обобщенная сила соответствующая обобщенной координате 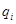 .
.
Если системе сообщить такое возможное перемещение, при котором одновременно изменятся все s обобщенных координат, то сумма элементарных работ на этом перемещении равна:
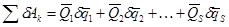 .
.
Это полная элементарная работа всех действующих на систему сил в обобщенных координатах.
Обобщенные силы - это величины равные коэффициентам при приращениях обобщенных координат в выражении полной работы действующих на систему сил.
Размерность обобщенной силы определяется размерностью обобщенной координаты:
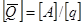 ;
; 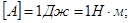 .
.
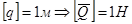 - сила;
- сила;
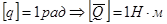 - момент силы (пары сил);
- момент силы (пары сил);
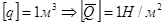 - давление.
- давление.
Порядок вычисления обобщенной силы:
– установить число степеней свободы системы;
– выбрать обобщенные координаты;
– изобразить все активные силы, включая силу трения;
– сообщить системе возможное перемещение, при котором изменится только 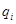 координата, получая положительное перемещение
координата, получая положительное перемещение 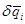 ;
;
– вычислить сумму элементарных работ всех сил на этом перемещении;
– определить обобщенную силу 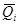 , соответствующую обобщенной координате
, соответствующую обобщенной координате 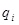 :
: 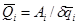 .
.
Дата добавления: 2016-01-29; просмотров: 3123;
