Обобщенная формула для изменения энтропии
Понятие «энтропии» предложено в середине 19-го столетия немецким физиком, «отцом термодинамического анализа» Рудольфом Клаузиусом, кото-рому историей науки отдается приоритет открытия второго закона термодина-мики. Однако автор не дал физического смысла энтропии. В течение полутора веков многими учеными предлагались различные толкования физического смысла энтропии. Каждое из них имело свои достоинства и недостатки. Однако достоверного общепризнанного толкования физического смысла энтропии нет и сегодня.
Опуская дискуссионные аспекты, связанные с понятием «энтропии», рассмотрим практические приложения энтропии в термодинамическом анализе.
Обобщенная формула для изменения энтропии:
,
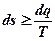где s – энтропия.
Знак равенства относится к обратимым процессам, а неравенства - к необратимым.
Энтропия – калорический параметр состояния и обладает всеми свойствами параметров.
1кг ‚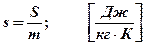 
m кг ‚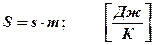 
.
"Тепловая смерть Вселенной" (Клаузиус): состояние всеобщего теплового равновесия, когда температура всех тел во Вселенной одинакова. Работа не совершается, тепло не передается от одного тела к другому, в том числе и живым организмам.
Таким образом, для обратимых процессов, которые мы и рассматриваем, формула для изменения энтропии имеет вид:
.
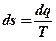Изменение энтропии в процессе является признаком теплового взаимодействия рабочего тепла с окружающей средой. Так как абсолютная температура Т всегда положительна, то знак теплоты определяется знаком энтропии. Процесс увеличения энтропии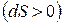 
означает подвод теплоты, а процесс уменьшения 
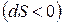– отвод теплоты от рабочего тела.
Тепловая энтропийная диаграмма
Наряду с p-v-координатами в термодинамике широко используются T-S-координаты, в которых по оси абсцисс откладывается энтропия. По оси ординат– температура.
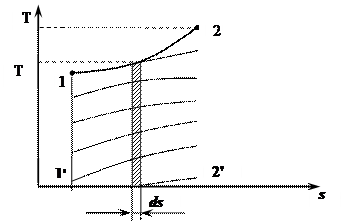
1-2 – произвольный процесс.
Площадь элементарного прямоуголь-ника =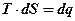 
.
Площадь фигуры под кривой процесса
пл.1-1'-2-2' =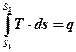 
Таким образом, в T-S координатах площадь под процессов эквивалентна теплу, подводимому или отводимому в процессе.
Изобразим произвольный цикл 1-а-2-b-1.
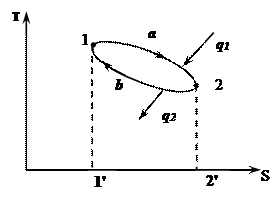
q1=площадь 1'-1-а-2-2' – подводимое тепло;
q2 = площадь 1'-1-b-2-2' – отводимое тепло;
q0=q1-q2= площадь 1-a-2-b-1-полезное тепло
Тогда
.
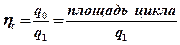Таким образом, к.п.д. цикла пропорционален площади цикла в T-S-координатах.
Основные термодинамические процессы
в T-S-координатах
Для того, чтобы использовать свойства тепловых энтропийных диаграмм, необходимо изображать в T-S-координатах процессы и циклы.
Изохорный процесс (v=const)
Тепло, подводимое в изохорном процессе, можно определить через теплоемкость (в дифференциальном виде):
dq = cv∙dT.
Подставим это выражение в общую формулу для изменения энтропии и проинтегрируем:
‚
→ 
‚
→ 
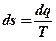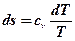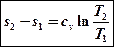
На основании этого выражения можно изобразить изохорный процесс в T-S-координатах.
|
Изохора в T-s- коорди-
натах изображается
логарифмической
кривой.
Изобарный процесс (p=const)
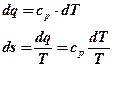
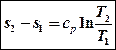
Изобара в T-s- координатах изображается логарифмической
кривой, лежащей положе изохоры.
Изотермический процесс (T=const)
Так как все тепло, подводимое в изотермическом процессе, расходуется на совершение работы, определим тепло по формуле для работы:
dq = dl = p∙dv ‚
Из уравнения состояния pv = RT выразим давление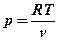 
и подставим его в формулу для тепла:
dq = p∙dv =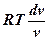 
‚
Подставим это выражение в общую формулу для изменения энтропии и проинтегрируем:
→
→ 
→
→ 
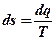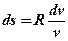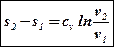
Сделав замену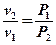 
, получим еще одну формулу:
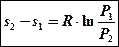
Адиабатный
процесс q=0;dq=0)
dq = 0 →
→ 
–
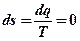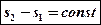
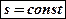
Иначе адиабатный процесс называют изоэнтропийным.
| |
Политропный процесс (pvn = const)
Тепло, подводимое в процессе, определим по первому закону термодинамики:
dq = du + dl ‚ (1)
Слагаемые в правой части определим по формулам:
du = cv∙dT; (2)
dl = p∙dv. (3)
Из уравнения состояния pv = RT выразим
p =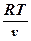 
и подставим в (3):
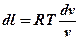(4)
Подставим (2) и (4) в (1):
→ 
.
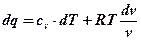Полученное выражение подставим в общую формулу для изменения энтропии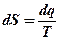 
:
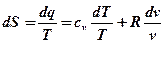
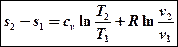
Как и сам политропный процесс, формула для определения изменения энтропии является обобщающей. После подстановки в нее условий протекания конкретного процесса, она принимает частный вид, соответствующий этому процессу. Убедимся в этом :
→ 
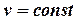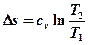; (т.к. 
).
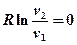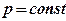→Сделаемзамену 
:
→ 
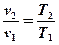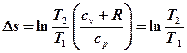, (т.к. cv + R = cp)
‚ 
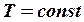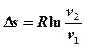(т.к. ).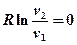
Еще одна формула для определения изменения энтропии политропного процесса:
|
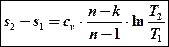
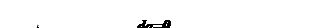
Политропа в T-S координатах изображается логарифмической линией, характер которой определяется значением показателя политропы п.
Цикл Карно вT=s координатах
Перенесем цикл Карно из p-v в T-s-координаты по процессам:
|
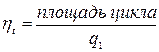, (т.е. кпд пропорционален площади цикла)
Цикл Карно в T-s- координатах изображается прямоугольником. Поскольку площадь прямоугольника всегда больше площади любой другой фигуры, вписанной в него, то к.п.д. цикла Карно в любом конкретном интервале температур будет иметь максимальное значение.
ТЕОРЕТИЧЕСКИЕ ЦИКЛЫ ДВИГАТЕЛЕЙ ВНУТРЕННЕГО
СГОРАНИЯ, ИХ КЛАССИФИКАЦИЯ И УПРОЩЕНИЯ ПРИ РАССМОТРЕНИИ ЦИКЛОВ
Идеи Карно по совершенствованию тепловых двигателей:
– использования в качестве рабочего тела продуктов сгорания, как имеющих максимальную температуру;
– предварительное сжатие горючей смеси перед воспламенением.
Дата добавления: 2016-01-29; просмотров: 1742;