Теплоемкость политропного процесса
Давление
Давление равно силе, действующей на единицу площади: 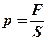 .
.
Абсолютное давление (pабс) отсчитывается от неусловного нуля.
Барометрическим (pбар) называют атмосферное давление.
Манометрическое давление (pман) равно разности между абсолютным и барометрическим (т.е. превышению над атмосферным). Измеряется манометром.
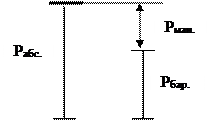 Тогда для определения абсолютного давления, заведомо большего атмосферного (pабс.> pбар), нужны барометр, манометр и формула: pабс = pбар +pман .
Тогда для определения абсолютного давления, заведомо большего атмосферного (pабс.> pбар), нужны барометр, манометр и формула: pабс = pбар +pман .
Вакуметрическое давление (Рвак) равно разности между барометрическим и абсолютным давлением (т.е. недостающему до атмосферного). Измеряется вакуметром.


Для определения абсолютного давления, заведомо меньшего атмосферного (pабс.< pбар), нужны барометр, вакуметр и формула: pабс = pбар - pвак
Если в формуле при символе давления нет индексов, то всегда подразумевается абсолютное давление.
Связь между различными единицами измерения давления:
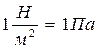 ; 1кПа = 103Па; 1МПа = 106Па;
; 1кПа = 103Па; 1МПа = 106Па;
1 бар = 105 Па = 750 мм рт. ст. = 1,02техн.атм.
1 техн. атм. = 1 кг/см2 = 104кг/м2; = 0,98∙105 Па = 0,98 бар =
= 735,6 мм рт. ст. = 10 м вод. ст.;
1 физ. атм. = 760 мм рт. ст. = 1,033 техн. атм.
Объём
Полный объём - V [м3].
Удельный объём – объём единицы массы вещества 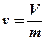 [м3/кг].
[м3/кг].
Удельный объем – величина, обратная плотности: 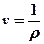 . Тогда
. Тогда 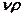 =1.
=1.
Температура
Параметром состояния является абсолютная температура. Отсчитывается по абсолютной шкале (шкале Кельвина). За 0 градусов этой шкале принята температура, при которой отсутствует тепловое движение элементарных частиц. Обозначается «Т», измеряется в градусах Кельвина (К°). Эту шкалу называют научной. В качестве практической шкалы в Европе применяется шкала Цельсия. За 0 градусов своей шкалы Цельсий принял температуру равновесия между водой и льдом, за 100 градусов – температуру равновесия между водой и насыщенным паром. Обозначается «t», измеряется в градусах Цельсия (С°). Связь между шкалами Кельвина и Цельсия: Т = t + 273,15°.
В США в качестве абсолютной шкалы используется шкала Ренкина. За 0 градусов этой шкалы, как и у Кельвина, принята температура, при которой отсутствует тепловое движение элементарных частиц, но цена градуса почти вдвое меньше: R=1,8K. В качестве практической шкалы используется шкала Фаренгейта. За 100 градусов своей шкалы Фаренгейт принял нормальную температуру человеческого тела. Цена градуса – как и у Ренкина. Связь со шкалой Цельсия: F=1,8·C+32.
Законы идеальных газов
Закон Бойля–Мариотта
Открыт в 1662 г. английским физиком Р.Бойлем и независимо от него в 1676 г. французским физиком Мариоттом:
при T=const произведение pv=const (или pV=const).
Закон Гей-Люссака
Открыт в 1802 году французским физиком Жозефом Луи Гей-Люссаком и практически одновременно англичанином Д.Дальтоном. Сам Гей-Люссак признавал, что за 15 лет до него этот же закон открыл его соотечественник Шарль, но результатов своих трудов не опубликовал. Поэтому в литературе закон иногда называют законом Шарля-Гей-Люссака, а то и просто Шарля.
При p = const отношение 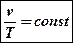 (или
(или 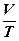 = const).
= const).
Если называть этот закон законом Шарля, то логично использовать запись:
при v = const отношение 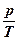 = const,
= const,
так как Шарль исследовал газы при v=const.
Объединенный закон Бойля–Мариотта и Гей-Люссака
В 1826 г. Гей-Люссак объединил свой закон с законом Бойля-Мариотта:
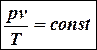 .
.
Уравнения состояния
Если в последней записи объединенного закона Бойля–Мариотта и Гей-Люссака обозначить const через R и несколько изменить форму записи, то получится уравнение состояния для 1 кг газа, предложенное в 1834 г. фран-цузским физиком Эмилем Клапейроном:
1 кг газа: pv = RT (ур-е Клапейрона для 1 кг газа),
где R – индивидуальная газовая постоянная, зависящая от природы газа.
Умножив правую и левую часть уравнения на массу газа m, получим:
pvm = mRT.
Но vm=V. Тогда еще одно уравнение примет вид:
m кг газа: pV = mRT (ур-е Клапейрона для m кг газа).
Умножив первое уравнение на молекулярную массу m[кг/кмоль], получим:
Pvm = mRT.
Но vm = vm ,где vm [м3/кмоль] -молекулярный объем(объем 1 кмоля). После замены получится третье уравнение состояния:
1 кмоль газа: pvm = mRT (ур-е Менделеева-Клапейрона для 1 кмоля газа).
Три приведенные уравнения состояния широко используются при решении задач.
Закон Авогадро
Еще один закон идеального газа: при одинаковых температурах и давлениях в равных объемах различных газов содержится одинаковое количество молекул.Гораздо чащепри решении задач используется следствие закона Авогадро: при одинаковых температурах и давлениях килограмм-молекулы различных газов занимают одинаковые объемы. Так, при нормальных физических условиях этот объем составляет:
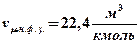 .
.
Условия, соответствующие нормальным физическим (н.ф.у.):
p = 760 мм рт.ст = 1,033 т.атм = 101325Па;
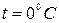 .
.
Но в задачах по термодинамике используются нормальные технические условия (н.т.у.). Им соответствуют:
p = 1 техн.атм = 1 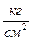 = 0,98 бар = 0,98·105 Па = 736,5 мм рт.ст.
= 0,98 бар = 0,98·105 Па = 736,5 мм рт.ст.
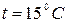 .
.
В этих условиях килограмм-молекула любого газа занимает объем:
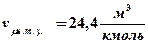 .
.
Газовая постояная
Из уравнения Менделеева-Клапейрона pvm = mRT выразим газовую постоянную:
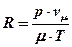 .
.
Но согласно объединенному закону Бойля-Мариотта и Гей-Люссака
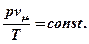
Для того, чтобы определить численное значение константы и единицы ее измерения, подставим в левую часть значения параметров, соответствующие одному из известных состояний вместе с их единицами измерения. Например, соответствующие нормальным техническим условиям:
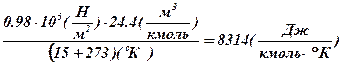 .
.
Тогда R = 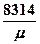 [
[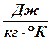 ].
].
По этой формуле легко определять значение газовой постоянной, не прибегая к справосным материалам.
Физический смысл газовой постоянной: она равна работе совершаемой 1кг газа при его нагревании на 10К при постоянном давлении.
Аргументацию физическому смыслу дадим позднее.
Равновесное состояние. Процесс. Равновесные и неравновесные процессы. Р–v -координаты.
Обратимые и необратимые процессы.
Равновесным называется такое состояние газа при котором температура и давление по всей его массе одинаковы.
Термодинамический процесс – это изменение состояния рабочего тела во времени, то есть изменение одного или нескольких его термодинамических параметров.
Равновесными называется процессы, протекающие через ряд равновесных состояний. Они возможны или при весьма медленном протекании процесса или при незначительном изменении параметров.
Все реальные процессы, протекающие в тепловых двигателях, быстротечны и неравновесны, однако теоретически изучаются как равновесные.
p-v – координаты:
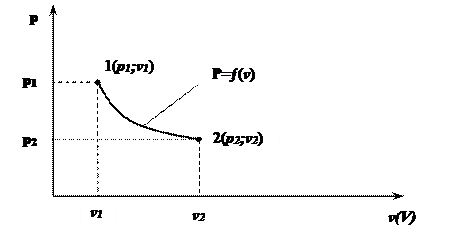
Равновесное состояние в p-v-координатах изображается точкой (1;2). Равновесный процесс – линией (1-2).
Обратимыми называются процессы, протекающие без потерь и после завершения которых рабочее тело возвращается в исходное состояние.
Все реальные процессы, протекающие в тепловых двигателях, являются необратимыми, однако теоретически изучаются как обратимые.
Теплоёмкость газов.
Теплоёмкость – это количество теплоты, которое необходимо подвести к единице количества вещества, чтобы нагреть его на 10К.
В зависимости от принятой единицы количества вещества различают теплоёмкости массовую, объемную и мольную.
Массовая теплоёмкость:
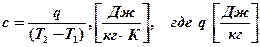 - тепло, подводимое к 1 кг газа.
- тепло, подводимое к 1 кг газа.
Объемная теплоемкость:
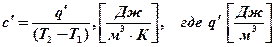 - тепло, подводимое к 1 м3 газа.
- тепло, подводимое к 1 м3 газа.
Мольная теплоемкость
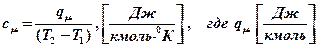 - тепло, подводимое к 1 кмолю газа.
- тепло, подводимое к 1 кмолю газа.
Эти виды теплоемкости связаны простыми соотношениями:
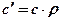 ;
; 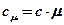 ;
; 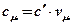 .
.
Теплоёмкость газа может иметь значение равное нулю или изменяться от – ∞ до + ∞ в зависимости от вида процесса, при котором подводится тепло. Она зависит от природных свойств газов и температуры. Теплоёмкость реальных газов зависит также от давления.
Зависимость теплоёмкости от температуры.
С увеличением температуры теплоёмкость газов увеличивается: с = f(t).
|
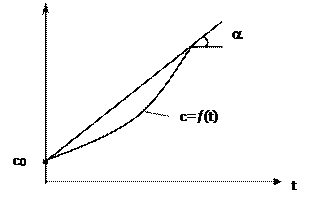 Для практических расчетов нелинейную зависимость достаточно аппрокси-мировать прямой линией. Ее уравнение:
Для практических расчетов нелинейную зависимость достаточно аппрокси-мировать прямой линией. Ее уравнение:
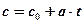 ;
;
где 
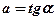 – угловой коэффициент
– угловой коэффициент
|
Зависимость теплоёмкости от вида термодинамического
процесса, в котором подводится тепло
Основные термодинамические процессы:
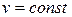 – изохорный (протекающий при постоянном объёме);
– изохорный (протекающий при постоянном объёме);
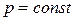 – изобарный;
– изобарный;
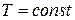 – изотермический (
– изотермический ( 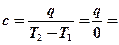 ∞);
∞);
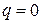 – адиабатный (тепло не подводится и не отводится от рабочего тела)
– адиабатный (тепло не подводится и не отводится от рабочего тела)
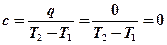 ;
;
pvn – политропный (обобщающий).
Поскольку изотермическая и адиабатные теплоемкости имеют тривиальные значения, а политропный процесс является обобщающим, остается определить теплоемкость при изохорном и изобарном подводе тепла.
В двух цилиндрах находится по одному килограмму одного и того же газа. Нагреем каждую порцию газа на 1°К. В первом случае – в изохорном процессе (поршень закреплен), во втором случае – в изобарном процессе (поршень нагружен телом постоянной массы). Обозначим подводимое тепло соответственно qv и qpи определим его через теплоемкость .
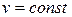
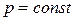


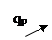 |
 qv
qv
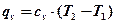
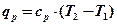
где сv – изохорная теплоёмкость; ср – изобарная теплоёмкость.
В изохорном процессе все подводимое тепло идет на нагревание рабочего тела, а в изобарном часть тепла расходуется на совершение работы. Поэтому 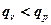 ;
;
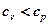 .
.
Поскольку все тепло, подводимое в изохорном процессе, расходуется на изменение температуры рабочего тепла, а в изобарном идет еще и на совершение работы, то при одинаковой разности температур в обоих процессах в изобарном следует подводить теплоты больше на величину работы совершаемой в этом процессе.
Но работа, совершаемая 1кг газа при его нагревании на 10К при постоянном давлении представляет собой физический смысл газовой постоянной (см. выше).
Тогда можно записать уравнение, связывающее изобарную и изохорную теплоемкости:
cp - cv = R – уравнение Майера.
В термодинамических расчетах широко используется отношение этих теплоемкостей:
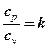 .
.
Примерные значения k:
для одноатомных газов (He; Ar; Xe) k = 1,6;
для двухатомных газов (О2; Н2; воздух) k = 1,4;
для многоатомных газов (CH4;CO2) k = 1,3.
Из последнего равенства выразим 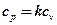 и подставим в уравнения Майера:
и подставим в уравнения Майера:
kcv – cv = R
Отсюда вытекают две формулы, по которым легко определить массовую изохорную и изобарную теплоемкости, считая их независящими от температуры:
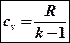 ;
;
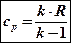 .
.
Если требуется определить теплоемкость с учетом ее зависимости от температуры, следует использовать формулу:
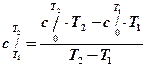 .
.
где T1 и T2– границытемпературного диапазона, для которого определяется теплоемкость;
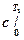 - теплоемкость в диапазоне от 0° до Т1 (берется из справочника);
- теплоемкость в диапазоне от 0° до Т1 (берется из справочника);
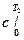 - теплоемкость в диапазоне от 0° до Т2 (берется из справочника).
- теплоемкость в диапазоне от 0° до Т2 (берется из справочника).
В заключении темы перечислим все разновидности теплоемкости, которые имеют нетривиальные значения:
массовая изохорная - сv; [Дж/кг·К] ;
массовая изобарная - ср; [Дж/кг·К] ;
объемная изохорная - 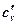 ;[Дж/м3·К];
;[Дж/м3·К];
объемная изобарная - 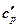 ;[Дж/м3·К];
;[Дж/м3·К];
мольная изохорная - сmv;[Дж/кмоль·К];
мольная изобарная - сmp;[Дж/кмоль·К].
ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
Сущность первого закона
 Подведем к 1 килограмму реального газа бесконечно малое количество теплоты dq. При нагревании газа увеличивается его температура и, следовательно, кинетическая энергия его молекул на величину dК. Увеличивается объем газа и совершается, таким образом, работа по преодолению сил сцепления между молекулами. Эта работа превращается в потенциальную энергию молекул, увеличивая ее на dП. При расширении газа совершается также внешняя работа dl. Тогда можно записать уравнение энергетического баланса:
Подведем к 1 килограмму реального газа бесконечно малое количество теплоты dq. При нагревании газа увеличивается его температура и, следовательно, кинетическая энергия его молекул на величину dК. Увеличивается объем газа и совершается, таким образом, работа по преодолению сил сцепления между молекулами. Эта работа превращается в потенциальную энергию молекул, увеличивая ее на dП. При расширении газа совершается также внешняя работа dl. Тогда можно записать уравнение энергетического баланса:
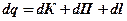 .
.
Поскольку сумма кинетической и потенциальной энергии молекул отражают внутреннее состояние газа, ее называют внутренней энергией газа и обозначают «U»:
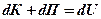
Используя эту замену, запишем несколько вариантов математической формулировки первого закона термодинамики:
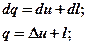
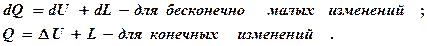
для 1кг газа; для m кг газа.
Словесная формулировка первого закона: тепло подводимое к газу, расходуется на изменение внутренней энергии и совершение внешней работы.
Внешняя работа газа.

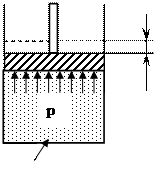 Если к 1 кг газа, находящемуся в цилиндре с подвижным невесомым поршнем, подвести бесконечно малое количество теплоты dq, то со стороны газа на поршень будет действовать давление p. Сила давления тогда будет равна:
Если к 1 кг газа, находящемуся в цилиндре с подвижным невесомым поршнем, подвести бесконечно малое количество теплоты dq, то со стороны газа на поршень будет действовать давление p. Сила давления тогда будет равна:
P = p∙S, где S – площадь поршня.
В результате поршень сместится на бесконечно малую величину dh. То есть будет совершена элементарная работа:
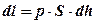 .
.
Но S ∙dh = dv . Тогда
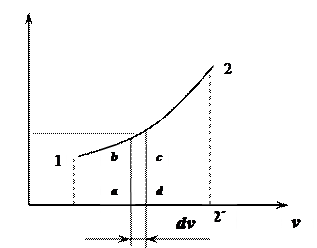
dl = p∙dv.
|
| |
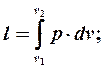
для полной работы:
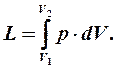
Графическая интерпретация работы
|
|
|
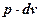 . А площадь всей фигуры под кривой процесса (1'-1-2-2') определится путем интегрирования:
. А площадь всей фигуры под кривой процесса (1'-1-2-2') определится путем интегрирования:
|
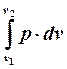 .
.
Но с другой стороны этот же интеграл равен работе, совершаемоей в процессе 1-2.
Таким образом в p-v-координатах работа эквивалентна площади под кривой процесса. То есть она является функцией процесса, а не параметром состояния рабочего тела.
Внутренняя энергия и ее свойства.
У идеального газа внутренняя энергия равна кинетической энергии его молекул. Т.е. U=f(K). Но кинетическая энергия молекул в свою очередь определяется температурой: K=f(T). Тогда можно утверждать, что внутренняя энергия однозначно зависит от температуры: U=f(Т).
Поскольку внутренняя энергия является функцией параметра состояния, то она сама является параметром.
І свойство внутренней энергии:
Внутренняя энергия – параметр состояния вещества и не зависит от характера процесса.
ІІ свойство внутренней энергии:
Поскольку внутренняя энергия зависит от температуры и не зависит от характера процесса, то в разных по характеру процессах с одинаковой разностью температур изменение внутренней энергии будет одинаковым.
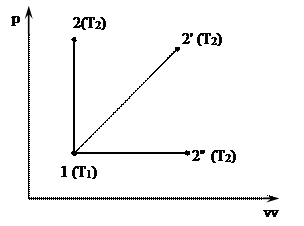
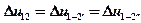
По I закону термодинамики
dq=du+dl.
Для изохорного процесса 1-2
dl=0; dq=du=cv(T2-T1).
.
На основании ІІ-го свойства внутренней энергии формулу, выведенную для изохорного процесса, можно распространить и на другие виды процессов с той же разностью температур:
Δu=cv(T2-T1).
Эта формула корректна для любого вида процесса.
Единицы измерения:
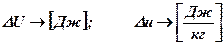
ЭНТАЛЬПИЯ
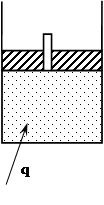
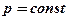 Подведем к 1 кг газа тепло q в изобарном процессе. По I закону термодинамики оно израсходуется на изменение внутренней энергии и совершений внешней работы:
Подведем к 1 кг газа тепло q в изобарном процессе. По I закону термодинамики оно израсходуется на изменение внутренней энергии и совершений внешней работы:
q = Du + l .
”Распишем” слагаемые в правой части:
Du = u2 – u1;
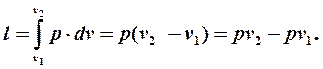
Подставим эти выражения в первую формулу и сгруппируем слагаемые:
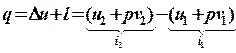 .
.
Однотипные выражения, стоящие в скобках, обозначим через i2 и i1 и назовем их энтальпией:
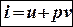 – энтальпия
– энтальпия
Физический смысл энтальпии: она представляет собой сумму внутренней энергии рабочего тела и энергии давления окружающей среды.
Так как энтальпия определяется через параметры состояния u, p, v, то она также является параметром состояния и ее изменение не зависит от характера процесса.
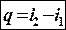 – формула корректна только для изобарного процесса (все тепло,
– формула корректна только для изобарного процесса (все тепло,
подводимое в изобарном процессе, расходуется на изменение
энтальпии);
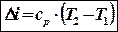 – формула корректна для любого вида процесса.
– формула корректна для любого вида процесса.
Обозначения и единицы измерения:
1кг ‚ 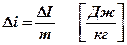 ;
;
m кг ‚ 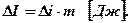 .
.
Внутренняя энергия, энтальпия – калорические параметры состояния.
Энтальпия используется для расчета изобарного процесса, который широко используется в технике.
Анализ основных термодинамических
процессов идеального газа.
Процессы исследуются по единому плану, не зависящему от характера процесса:
а) выводится уравнения процесса в p-v-координатах; дается его
графическое изображение;
б) выводятся уравнения, связывающие начальные и конечные значения
переменных параметров в данном процессе;
в) определяется внешняя работа газа в процессе;
г) определяется тепло, подводимое или отводимое в процессе;
д) определяется изменение внутренней энергии и энтальпии.
Изохорный процесс (v=const)
А)
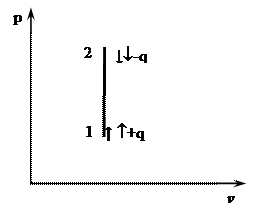 Линия изображающая изохорный процесс называется изохорой.
Линия изображающая изохорный процесс называется изохорой.
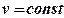 – уравнение процесса
– уравнение процесса
Б)
Запишем уравнения состояния для точек 1 и 2:
p1v1 = RT1 ;
p2v2 = RT2 .
Разделим почленно первое уравнение на второе:
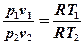 ;
;
После сокращений получим:
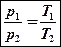 .
.
В)
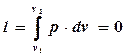 , т.к. dv=0. l=0
, т.к. dv=0. l=0
Г)
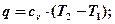
q=Du + l, но l=0, тогда
q = Du.
Особенностью изохорного процесса является то, что все тепло подводимое в нем, расходуется на измерение внутренней энергии.
д)
Du = cv∙(T2 – T1);Di = cp∙(T2 – T1).
Изобарный процесс (p=const)
а)
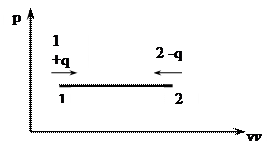
р = const–уравнение процесса
Линия изображающая изохорный процесс называется изохорой.
б)
Запишем уравнения состояния для точек 1 и 2:
p1v1 = RT1 ;
p2v2 = RT2 .
Разделим почленно первое уравнение на второе:
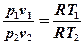 ;
;
После сокращений получим:
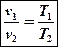 .
.
в)
Общую формулу для определения работы проинтегрируем с учетом того, что р = const:
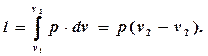
l = p(v2-v1)
Если в этом выражении открыть скобки сделать замены pv2 = RT2 и pv1 = RT1, nj получим еще одну формулу для определения работы:
l = R(T2 – T1)
г)
Тепло, подводимое или отводимое в изобарном процессе, можно определить тремя способами:
q = cp(T2 – T1);
q = Du + l;
q = i2 – i1.
Особенность изобарного процесса: только в нем подводимое тепло расходуется по двум пунктам – идет на изменение внутренней энергии и совершение работы.
д)
Du = cv∙(T2 – T1); Di = cp∙(T2 – T1).
Изотермический процесс (T = const)
а) 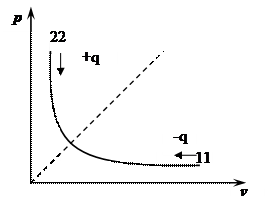
Для вывода уравнения процесса используем уравнение состояния:
pv = RT.
Поскольку для изотермического процесса RT = const, можно записать:
pv = const - уравнение процесса.
Изотерма в p-v-координатах изображается равнобокой гипер-болой (симметричной относительно бисектрисы прямого угла).
Б)
Т.к. pv = const, то p1v1 = p2v2 . Отсюда
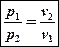 .
.
В)
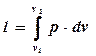
Из уравнения состояния pv = RT выразим р: p = RT/v. Подставим в правую часть равенства и проинтегрируем полученное выражение:
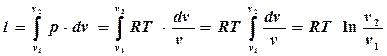 .
.
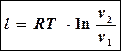
Но в изотермическом процессе 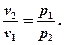 После замены в подлогарифменном выражении получится еще одна формула для определения работы:
После замены в подлогарифменном выражении получится еще одна формула для определения работы:
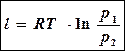
Заменив в последнем выражении RT через p1v1 (из уравнения состояния p1v1 =RT) , можно записать третью формулу:
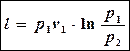
Г)
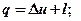
Но в изотермическом процессе Du = cv∙(T2 – T1)=0, т.к. T2 = T1. Тогда
q = l.
Особенностью изотермического процесса является то, что все тепло, подводимое в нем, расходуется на совершение работы. Являясь в этой связи идеальным процессом для тепловых двигателей, изотермический процесс на практике, однако, не осуществим. Поэтому он не задействован ни в одном цикле теплового двигателя.
д)
Du = cv∙(T2 – T1)=0 Di = cp∙(T2 – T1)=0
Адиабатный процесс (q = 0; dq = 0)
Адиабатным называется процесс, при котором тепло не отводится и не подводится к рабочему телу. Практически полное отсутствие теплообмена возможно лишь при высокой скорости протекания процесса, когда рабочее тело просто не успевает обменяться теплом с окружающей средой или другими телами. Адиабатный процесс является основным процессом любого теплового двигателя, так как именно при его протекании внутренняя энергия рабочего тела превращается в работу.
а)
Выведем уравнение адиабатного процесса в p-v-координатах.
Запишем 1-й закон термодинамики в дифференциальной форме:
dq = du + dl.
Для адиабатного процесса
du + dl = 0 (1)
Слагаемые в левой части определим по формулам:
du = cv∙dT (2)
dl = p∙dv (3)
Продифференцируем уравнение состояние pv = RT по температуре с учетом того, что p и v являются функциями температуры:
p∙dv + v∙dp = R∙dT
Отсюда 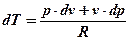 (4)
(4)
Из темы «Теплоемкость газов» (см. выше) известно:
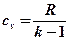 (5)
(5)
Подставим выражения (4) и (5) в (2). После сокращения R получим:
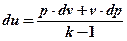 (6)
(6)
Подставим (6) и (3) в формулу (1):
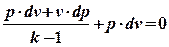 .
.
Умножим правую и левую части уравнения на (k-1):
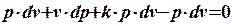 .
.
После взаимного уничтожения первого и последнего слагаемого получим:
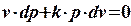
Разделим обе части уравнения на pv. После сокращений получим:

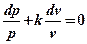 .
.
Проинтегрируем полученное выражение и сделаем некоторые преобразования:
lnp + k∙lnv = const;
lnp + lnvk = const;
lnpvk = const.
Пропотенцируем последнее выражение:
pvk = const
Полученное выражение и является уравнением адиабатного процесса.
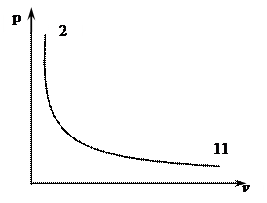
Адиабата в p-v-координатах изображается неравнобокой гиперболой, идущей круче изотермы.
Б)
В адиабатном процессе все три термодинамических параметра – p, v, и T являются переменными. Поэтому количество соотношений, связывающих их попарно, должно быть равно трем.
Первое вытекает из уравнения процесса pvk = const, на основании которого можно записать p1v1k = p2v2k. Отсюда
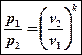 (7)
(7)
Запишем уравнения состояния для 1-й и 2-й точки процесса и разделим почленно первое уравнение на второе:
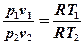 (8)
(8)
сократим R и подставим сюда (7):

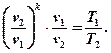
После преобразования получим:
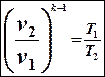
Из (7) выразим отношение объемов:
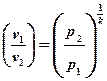
 и подставим в (8).
и подставим в (8).
После преобразований получим:
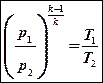
В)
По 1-му закону термодинамики q = Du + l. Но у адиабатного процесса q = 0. Тогда
l = -Du,
т.е работа в адиабатном процессесовершается за счет внутренней энергии.
Используя формулы Du = cv(T2 – T1); 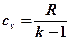 ; p1v1 = RT1; p2v2 = RT2 , можно записать несколько выражений для определения работы:
; p1v1 = RT1; p2v2 = RT2 , можно записать несколько выражений для определения работы:
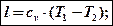
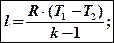
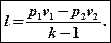
г) 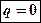
Д)
Du = cv∙(T2 – T1)=0 Di = cp∙(T2 – T1)=0
Политропный процесс
Политропными называются процессы подчиняющиеся уравнению:
pvn = const,
где n – показатель политропы (- ∞ < n < + ∞).
Политропный процесс является обобщающим. Он включает все термодинамические процессы, протекающие с постоянной теплоемкостью. Каждому из таких процессов соответствует свое значение показателя политропы. Частными случаями политропного процесса является и основные термодинамические процессы. Убедимся в этом:
А)
n = 0 → pv0 = const → p = const → изобарный процесс;
n = 1 → pv1 = const →‚ pv = const → изотермический процесс;
n = k → pvk = const → адиабатный процесс;
n = 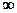 →pv¥=const →
→pv¥=const → 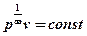 → v = const → изохорный процесс.
→ v = const → изохорный процесс.
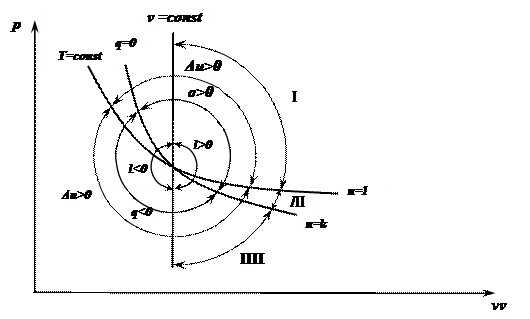
Показатель политропы во многом определяет характер протекания процесса, позволяет судить о распределении энергии в процессе. Для иллюстрации разобьем основными термодинамическими процессами координатную плоскость на секторы и рассмотрим особенности процессов расширения в зависимости от значения показателя политропы.
; .
|
| |
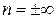 ) характеризуются положительной работой (
) характеризуются положительной работой ( 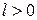 ), так как сопровождаются расширением рабочего тела; для процессов, находящихся левее изохоры, характерна отрицательная работа.
), так как сопровождаются расширением рабочего тела; для процессов, находящихся левее изохоры, характерна отрицательная работа.
Процессы расположенные правее и выше адиабаты ( 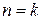 ) идут с подводом теплоты (
) идут с подводом теплоты ( 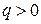 ), а левее и ниже адиабаты – с отводом теплоты (
), а левее и ниже адиабаты – с отводом теплоты ( 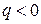 ).
).
Процессы, расположенные выше изотермы ( 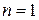 ), характеризуются увеличением внутренней энергии (Du>0), а ниже изотермы – уменьшением внутренней энергии (Du<0).
), характеризуются увеличением внутренней энергии (Du>0), а ниже изотермы – уменьшением внутренней энергии (Du<0).
Процессы, расположенные между адиабатой и изотермой ( 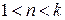 ), имеют отрицательную теплоемкость, так как теплота и внутренняя энергия имеют противоположные знаки.
), имеют отрицательную теплоемкость, так как теплота и внутренняя энергия имеют противоположные знаки.
Особенности трех групп процессов расширения
| № п/п | n | q | Δu | l | Схема энергетического Баланса | ||||
| I | – ∞ < n < 1 | q > 0 | Δu > 0 | l > 0 |

| ||||
| II | 1 < n < k | q > 0 | Δu < 0 | l > 0 |

| ||||
| III | k < n < + ∞ | q < 0 | Δu < 0 | l > 0 |

|
I. Подводимое тепло расходуется на увеличение внутренней энергии и совершение работы.
II. Работа совершается за счет подводимого тепла и за счет внутренней энергии.
III. Тепло отводится и совершается работа за счет внутренней энергии.
Б)
Так как структура уравнений политропного и адиабатного процессов аналогична, формулы соотношений переменных параметров и работы адиабатного процесса можно принять и для политропного после замены показателя степени k на n:
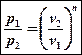

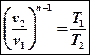

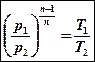
В)
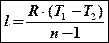
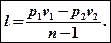
Г)
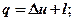
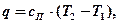
где сП – теплоемкость политропного процесса.
Д)
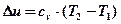
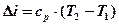
Теплоемкость политропного процесса
Выведем формулу для теплоемкости политропного процесса. Для этого запишем I-й закон термодинамики:
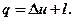
Подставим сюда формулы:
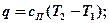
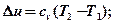
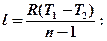
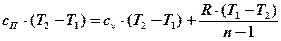 .
.
Сократим скобки, заменим 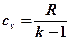 и выразим отсюда cП:
и выразим отсюда cП:
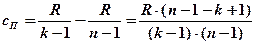 .
.
Сделав обратную замену 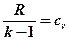 , получим формулу для определения теплоемкости политропного процесса:
, получим формулу для определения теплоемкости политропного процесса:
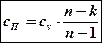
Как и сам политропный процесс формула для определения его теплоемкости является обобщающей. По ней можно определить теплоемкость любых процессов, в том числе и основных термодинамических. Подставим в нее значения показателя политропы, соответствующие основным процессам:
Изобарный процесс → 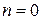 ; →
; → 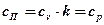 ;
;
Изотермический процесс → 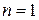 ; →
; → 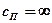 ;
;
Адиабатный процесс → 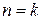 ; →
; → 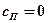 ;
;
Изохорный процесс → 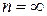 ; →‚
; →‚ 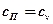 .
.
Во всех случаях получены значения теплоемкости, соответствующие условиям протекания каждого из основных процессов.
ГАЗОВЫЕ СМЕСИ.
В большинстве тепловых двигателей рабочими деталями являются газовые смеси (продукты сгорания).
Газовая смесь – это газ, состоящий из двух или более компонентов, не вступающих друг с другом в химические реакции.
Для каждого компонента в отдельности и для смеси в целом применимы газовые законы и уравнения состояния.
Далее приняты обозначения:
p, Т, V – параметры смеси.
pі – давление і–го компонента при объеме и температуре смеси (парциальное давление).
Vі – объем і – го компонента при давлении и температуре смеси (парциальный объем).
Температуры всех компонентов и смеси в целом одинаковы.
Дата добавления: 2016-01-29; просмотров: 10637;
