Кажущаяся молекулярная масса смеси
Плотность газа можно определить из соотношения
→,
где m - молярная масса, vm - молярный объем газа.
Подставим это соотношение в формулу
→
→ 
.
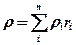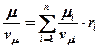«При одинаковых температурах и давлениях килограмм-молекулы различных газов занимают одинаковые объемы» - следствие закона Авогадро. На его основании можно сократить vm и vmi . Получим:
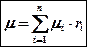
Или, в развернутом виде:
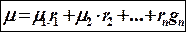
Через массовые доли m можно определить по формуле:
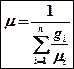
Газовую смесь можно считать однородным газом с молекулярной
массой, рассчитанной по одной из этих формул. (Ее называют
«кажущейся».)
Молекулярная масса воздуха, рассчитанная по приведенным
формулам, составляет 29 кг/кмоль.
Перевод массовых долей в объемные и обратно (без вывода)
массовые доли ‚ в объемные
; 
;
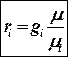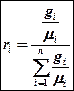объемные доли ‚ в массовые
; 
.
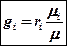ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
Сущность и формулировки
Принципиальная модель теплового двигателя
Второй закон имеет много формулировок. Некоторые из них:
Для получения из теплоты работы необходимо иметь разность температур. (С. Карно, 1824г.).
Теплота не может переходить от холодного тела к горячему самопроизвольно, то есть без затрат работы. (Р. Клаузиус, 1850г.).
Невозможно получение работы без перехода части теплоты от горячего источника к холодному. (В. Томсон, 1851г).
Все самопроизвольные процессы протекают в направлении от состояний менее вероятных к состояниям более вероятных. (Л. Больцман,1897г.).
Вечный двигатель второго рода невозможен.
Вечный двигатель второго рода– машина, которая не имеет источника холодного источника тепла и умеет извлекать работу из равновесной термодинамической системы. С помощью такой машины можно было бы превращать в работу внутреннюю энергию окружающей среды.
Теплота состоит из эксергии и анергии. (Современная формулировка)
Круговые процессы (циклы)
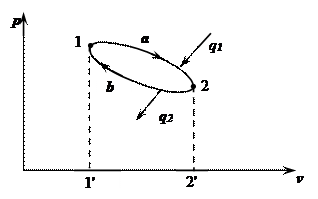
При протекании процесса расширения 1-а-2 совершается работа
l1 = площадь 1'-1-а-2-2'.
Рабочее тело возвращается в исходное состояние процессом 2-b-1, на совершение которого затрачена работа:
l2 = площадь 1'-1-b-2-2'.
Круговым процессом (циклом) называется совокупность двух или более процессов, возвращающих рабочее тело в исходное состояние.
Полезная работа цикла эквивалентна площади цикла в p-v координатах.
l0 = площадь 1-а-2-b-1.
Цикл можно разбить на участки в зависимости от того, подводится или отводится тепло к рабочему телу:
q1 – подводимое тепло (1-а-2);
q2 – отводимое тепло (2-b-1);
q0 – полезное тепло цикла.
Очевидно,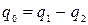 
.
Запишем 1-й закон термодинамики для цикла:
q0 = Du0 + l0.
Поскольку рабочее тело возвращается в исходное состояние, то Du0=0.
Тогда
q0 = l0.
Отношение работы произведенной двигателем за цикл к количеству теплоты, подведенной за этот цикл называется термическим КПД.
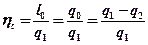
– термический КПД
ht определяет степень термодинамического совершенства цикла.
Циклы прямые и обратные,
обратимые и необратимые
Прямыми называются циклы, в которых процессы направлены по часовой стрелке, причем процессы расширение располагаются над процессами сжатия. (См. цикл выше.)
Полезная работа в цикле положительна, совершается за счет подводимой теплоты. По этим циклам работают тепловые двигатели.
Обратными называются циклы, в которых процессы направлены против часовой стрелки, причем процессы расширения располагаются под процессами сжатия.
Полезная работа в циклах отрицательна, компенсируется за счет притока энергии извне. По этим циклам работают холодильные установки.
Обратные циклы состоят из обратимых процессов. Необратимость одного процесса делает весь процесс необратимым.
Цикл Карно для идеального газа
Цикл предложен в 1824г. французским ученым С. Карно. Он является идеальным циклом тепловых двигателей. Особенность цикла заключается в том, что тепло в нем подводится и отводится в изотермических процессах.
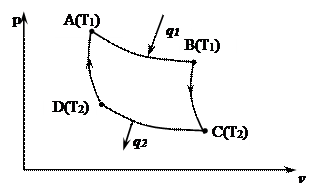
(AB) →изотермическое расширение с подводом теплоты q1;
(ВС) → адиабатное расширение;
(СD) →изотермическое сжатие с отводом теплоты q2;
(АD) → адиабатное сжатие.
Выведем формулу для определения к.п.д. цикла Карно htk .
Исходнаяформула:
.
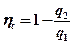Для изотермического процесса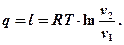 
Тогда тепло, подводимое и отводимое в цикле Карно, можно определить по аналогичным формулам:
; 
‚ 
.
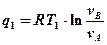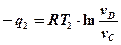Подставим q1 и q2 в исходную формулу:
.
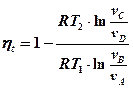Докажем, что кроме газовой постоянной можно сократить и лога-рифмы. Для этого следует доказать, что подлогарифменные выражения равны.
Для адиабатных процессов BC и DA можно записать:
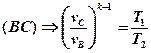(1); 
.
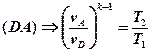Второе выражение возведем в степень -1:
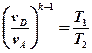(2).
В выражениях (1) и (2) равны правые части. Следовательно, равны и левые:
.
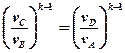Отсюда
‚ 
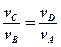, что и требовалось доказать .
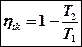– КПД цикла Карно
Свойства КПД Карно:
1. КПД не зависит от природы рабочего тела, а зависит от температур горячего и холодного источника тепла.
2. КПД увеличивается при увеличении перепада температур в цикле.
3. 
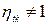, т.к. 
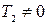, а 
.
4. 
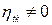, т.к. 
.
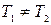Цикл Карно на практике неосуществим, но он имеет большое научное значение, так как в любом конкретном интервале температур этот цикл дает максимально возможный КПД. (Докажем это утверждение позже.) Поэтому КПД цикла Карно служит эталоном для оценки степени совершенства любого цикла любого теплового двигателя.
Практическое значение цикла Карно состоит в том, что он указывает на необходимость увеличения Т1 и уменьшения Т2 для повышения КПД двигателя.
Обратный цикл Карно
|
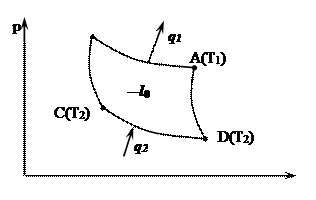
(AB); (СD) – изотермы;
(ВС); (DА) – адиабаты.
|
ЭНТРОПИЯ
Дата добавления: 2016-01-29; просмотров: 8932;