Паутинообразная модель

Проведенный анализ зависимости рыночного равновесия от времени основывался на методе сравнительной статики, при котором сопоставляются несколько разновременных равновесных состояний без рассмотрения процесса перехода от одного равновесия к другому. Описание процессов, происходящих во времени, осуществляется посредством динамического анализа, в котором цена и выпуск являются функциями от времени. Рассмотрим одну из простейших динамических моделей ценообразования - «паутинообразную» модель.

В этой модели принимается во внимание, что при планировании объемов рыночной сделки потребители и производители могут оказаться в неодинаковом положении. Покупатель, планируя в периоде t объем спроса, знает цену в этом периоде, а производитель в момент осуществления мероприятий, определяющих объем его предложения, не имеет представления, какова будет цена к моменту выхода продукции на рынок. Так, фермер, определяя площади посева, не знает цену урожая в день его реализации; когда производитель мебели определяет объем ее выпуска, ему еще неизвестно, по какой цене ее можно будет продать, и т.п.

В «паутинообразной» модели ценообразования предполагается, что ожидаемая производителями в периоде (t - 1) цена в период t равна существующей цене. Иначе говоря, производитель принимает сегодня решение об объеме продаж завтра на основе сегодняшней цены.

Таким образом, в «паутинообразной» модели объем рыночного спроса в периоде t зависит от цены этого периода: Q_t^D = a - bP_t, а объем рыночного предложения в данном периоде определяется ценой предшествовавшего периода: Q_t^S = m + nP_t-1.

Паутинообразная модель - модель, изображающая траекторию движения к состоянию равновесия, когда реакция предложения или спроса запаздывает.

Паутинообразная модель описывает динамический процесс: траекторию корректировки цен и объема производства при движении от одного состояния равновесия к другому; используется для описания колебаний цен на рынках сельскохозяйственной продукции, на биржевом рынке, где предложение реагирует на изменения цен с некоторым запозданием.

Рассмотрим вариант динамической модели рынка одного продукта. Предположим, что объем спроса зависит от уровня цен текущего периода, а объем предложения - от уровня цен предшествующего периода:

Q_i^D=Q_i^D(P_t), Q_i^D = Q_i^S(P_t-1), (43)

где t - определенный период (t = 0,1,2,..., Т). Это значит, что производители в период t - 1 определяют объем производства, предполагая, что цены периода t - 1 сохраняются и в период t (P_t-1 = P_t).

В таком случае график спроса и предложения будет иметь вид паутинообразной модели.

Возможны три варианта изменения рыночной цены во времени.

1. Если наклон линии предложения более крутой, чем наклон линии спроса, то со временем отклонение от равновесия уменьшается, равновесие восстанавливается (Рисунок 61).

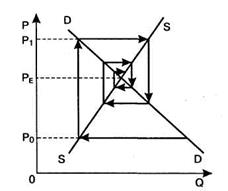
Рисунок - 61

2. Если наклон линии предложения более пологий, чем наклон линии спроса, отклонение от равновесия увеличивается (Рисунок 62).

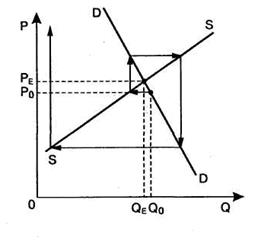
Рисунок - 62

3. При одинаковом наклоне линий предложения и спроса рынок колеблется вокруг точки равновесия (Рисунок 63). Этот вариант рассмотрим несколько подробнее. Допустим, что начальная цена Ро. На эту цену ориентируются производители в период t = 1, предлагая продукцию в объёме Q1, что ниже равновесного уровня QE. Тогда возникает дефицит, в результате чего цены повышаются до P1. В ответ на это производители увеличат объем предложения до Q2, надеясь, что уровень цен сохранится и в период t = 2. Избыток предложения приведет к понижению цены до Ро и т. д.

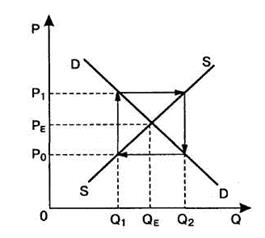
Рисунок – 63

Следовательно, несмотря на то, что линии спроса и предложения имеют нормальный наклон, запаздывание в реакции предложения на изменение цен может привести к нестабильности равновесного состояния. Из этого вытекает, что анализ стабильности не ограничивается только методом сравнительной статики.

Все три варианта допускают неизменность функций спроса и предложения во времени.