Производственный процесс в краткосрочном периоде

В действительности за короткий период времени одни виды затрат изменяются больше, чем другие. От степени, в которой изменяются различные виды затрат в течение короткого периода времени, зависит увеличение объёма выпуска. Например, в любой момент времени на фабрике есть определённая площадь производственных помещений и данное количество станков. В течение короткого времени производство может быть увеличено, если фабрика будет работать круглые сутки. Большее количество рабочих можно привлечь для работы в две или три смены каждый день. Так можно работать все семь дней в неделю, если необходимо, и существует большой спрос на производимую продукцию. В этом случае соотношение применяемого труда к капиталу увеличится.

Для простоты анализа предположим, что в течение некоторого периода времени фирма изменяет затраты только одного фактора производства – труда (L) Затраты всех остальных факторов остаются неизменными. Тогда объём выпуска ( y) становится функцией от одной переменной – количества трудозатрат (L): y = f(L)

В теории краткосрочного периода объём выпускаемой фирмой продукции часто называют совокупным (общим) продуктом переменного фактора производства (в нашем случае – труда) и обозначают TP. Однако в микроэкономическом анализе важны не столько общие показатели, сколько средние и предельные величины.

Средний переменный продукт фактора производства – это отношение совокупного продукта переменного фактора к использованному количеству этого фактора. Например, средний продукт труда APL − это совокупный продукт, делённый на количество часов труда (L):

. (17)

Приведённая величина представляет собой производительность труда в форме объёма выпуска за каждый час труда.

Предельный продукт переменного фактора это предельная производительность.

Предельный продукт труда 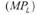показывает, как изменится общий продукт труда при изменении трудозатрат на одну единицу и при прочих равных условиях. Он может быть легко подсчитан по следующей формуле:

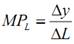. (18)

где ∆y − изменение в общем продукте (в объёме выпуска продукции);

∆L − изменение в затратах труда.

Можно также сказать, что предельный продукт труда показывает производительность последнего нанятого работника. Отсюда его другое название – предельная производительность труда.

Закон уменьшающейся предельной производительности переменного фактора производства (во многих учебниках он именуется также законом убывающей отдачи переменного фактора).

Впервые этот закон был сформулирован во второй половине XVIII в. французским экономистом Тюрго в связи с исследованием сельскохозяйственного производства.

"Семена, брошенные в плодородную землю, но без всякой ее обработки, — пишет он, — почти наверняка пропадут впустую. Если прилагать труд, то урожай будет возрастать: сначала в большей пропорции, чем рост труда, затем в меньшей — вплоть до того момента, когда земля полностью истощится. Искусство земледельца уже ничего не сможет добавить к этой картине, возрастание затрат не даст теперь никакой прибавки продукции".

Д. Рикардо использовал закон убывающей производительности для объяснения установления цен на зерно в Великобритании в период после 1814 г.: в процессе развития земледелия удельная производительность сельского хозяйства падала, а издержки производства росли, что приводило к увеличению цен.

Первоначально утверждали что это правило справедливо только для сельскохозяйственного производства. Современная экономическая наука считает, что закон убывающей производительности носит всеобщий характер и относится к любой человеческой деятельности, которая использует два или более факторов производства, и количество одного из них непрерывно увеличивается, а другого (других) остается неизменным. В общем виде его смысл можно передать следующим образом. Если некоторые или хотя бы один из факторов производства, которые используются в производственном процессе, являются фиксированными в течение некоторого промежутка времени (например, количество станков предприятия может не изменяться в течение года), тогда предельная производительность переменных факторов производства либо сразу, либо начиная с определённого момента, непременно начнёт снижаться. В нашем случае переменным фактором производства является труд, так как мы изменяем количество затрачиваемого труда, нанимая дополнительных работников. Последовательное привлечение дополнительных работников при фиксированном количестве станков хотя и будет увеличивать выпуск продукции фирмы, однако этот прирост продукции от работы каждого следующего нанимаемого работника окажется меньше по сравнению с тем приростом продукции, который был получен фирмой от работы предыдущего нанятого ею работника. Это означает, что предельная производительность, т.е. продукт последнего нанятого работника (предельный продукт труда) убывает по мере увеличения числа работников на фирме.

Здесь нужно обратить особое внимание на два обстоятельства. Во-первых, закон убывающей предельной производительности действует только в том случае, если несколько или хотя бы один из используемых фирмой факторов производства (например, земля или капитал) остаются фиксированными в течение определённого периода времени. Если же все факторы производства являются переменными (т.е. их количество изменяется), тогда этот закон перестаёт действовать. В самом деле, если бы в предыдущем примере мы могли изменить количество лопат, а затем и количество земли, засаженное картофелем, то всем пятидесяти ребятам нашлось бы дело и их производительность возросла бы.

Во-вторых, этот закон относится не только к убыванию предельной производительности труда. Аналогичным образом он действует применительно к любому другому фактору производства, являющемуся переменным. Например, если у вас фиксированы затраты труда, но при этом вы наращиваете количество сырья и материалов, используемых в процессе производства продукта, то материалоотдача от каждой дополнительной единицы затрат сырья будет снижаться.

Теория производства изучает прежде всего соотношение между количеством применяемых ресурсов и объемом выпуска. Методологически теория производства во многом схожа с теорией потребления, однако с тем отличием, что основные ее категории имеют не субъективно-психологическую основу, а объективную природу и могут быть квантифицированы, т. е. измерены, в определенных единицах.

Изокванта (равный выпуск) - кривая, демонстрирующая различные варианты комбинаций факторов производства, которые могут быть использованы для выпуска данного объема продукта. Изокванты иначе называют кривыми равных продуктов, или линиями равного выпуска.

Наклон изокванты выражает зависимость одного фактора от другого в производственном процессе. При этом увеличение одного фактора и уменьшение другого не вызывает изменений в объеме выпускаемой продукции. Данная зависимость изображена на рисунке 32.

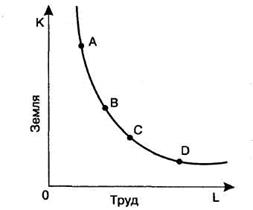
Рисунок 32 - Изокванта

Положительный наклон изокванты означает, что увеличение применения одного фактора потребует увеличения применения другого фактора, чтобы не сократить выпуск продукции. Отрицательный наклон изокванты показывает, что сокращение одного фактора (при определенном объеме производства) всегда будет вызывать увеличение другого фактора.

Изокванты выпуклы в направлении начала координат, поскольку хотя факторы могут быть заменяемы один другим, однако они не являются абсолютными заменителями.

Кривизна изокванты иллюстрирует эластичность замещения факторов при выпуске заданного объема продукта и отражает то, насколько легко один фактор может быть заменен другим. В том случае, когда изокванта похожа на прямой угол, вероятность замещения одного фактора другим крайне невелика. Если же изокванта имеет вид прямой линии с наклоном вниз, то вероятность замены одного фактора другим значительна.

Чем дальше от начала координат расположена изокванта, тем больший объем выпуска она представляет. Крутизна наклона изокванты выражает предельную норму технического замещения (MRTS), которая измеряется соотношением изменения объема выпуска продукции. Предельная норма технической замены фактора Y фактором X (MRTSxy) –это количество фактора Y (например, капитала), от которого можно отказаться при увеличении фактора X (например, труда) на 1 ед., чтобы выпуск не изменился (остаемся на прежней изокванте).

Предельная норма технического замещения трудом капитала (MRTSLK) определяется величиной капитала, которую может заменить каждая единица труда, не вызывая изменения объема выпуска продукции. Предельная норма технического замещения в любой точке изокванты равна наклону касательной в этой точке, умноженному на -1:

MRTS_LK dK/dL | Q = const. (19)

Изокванты могут иметь различную конфигурацию: линейную, жесткой дополняемости, непрерывной замещаемости, ломаной изокванты.

Линейная изокванта - изокванта, выражающая совершенную замещаемость факторов производства (MRTS_LK = const).

Жесткая дополняемость факторов производства представляет такую ситуацию, при которой труд и капитал сочетаются в единственно возможном соотношении, когда предельная норма технического замещения равна нулю (MRTS_LK = 0), так называемая изокванта леонтьевского типа (Рисунок 33).

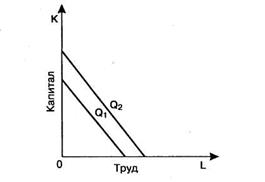
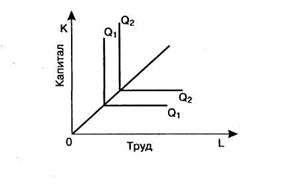
Рисунок 33 - Жесткая изокванта

На практике наиболее реалистичной (характерной для большинства современных производств) считают ломаную изокванту, предполагающую лишь несколько методов производства (Р) (Рисунок 34).

Рисунок 34 – Ломаная изокванта

Карта изоквант представляет собой набор изоквант, каждая из которых иллюстрирует максимально допустимый объем производства продукции при любом данном наборе факторов производства. Карта изоквант является альтернативным способом изображения производственной функции.

Смысл карты изоквант аналогичен смыслу карты кривых безразличия для потребителей. Карта изоквант схожа с контурной картой горы: все большие высоты показаны посредством кривых.

Карта изоквант может быть использована для того, чтобы показать возможности выбора среди множества вариантов организации производства в рамках короткого периода, когда, например, капитал является постоянным фактором, а труд - переменным фактором.

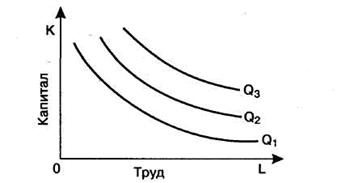
Рисунок 35 - Карта изоквант

В краткосрочном периоде, когда один из факторов может быть переменным, а другие — постоянными, расширение производства подчиняется принципу убывающей отдачи переменного фактора.

В долгосрочном периоде, когда фирма может изменять все факторы производства, действует принцип экономии от масштаба. Если при данной технологии увеличение выпуска осуществляется за счет пропорционального увеличения всех производственных ресурсов, то происходит изменение масштабов производства.

Допустим, производственная функция первоначального выпуска имеет вид:

Q0=f(K,L). (20)

Тогда после увеличения количества применяемых ресурсов N раз производственная функция будет выглядеть так:

Q2=f(NK,NL). (21)

При этом рост объема производства может быть различным:

а) если вместе с ростом факторов производства в N раз выпуск также увеличится в N раз 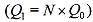, то отдача от масштаба постоянна;

б) если выпуск увеличится менее чем в N раз 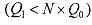, то имеет место убывающая отдача от масштаба;

в) если выпуск увеличится более чем в N раз 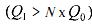, то имеет место возрастающая отдача от масштаба.

Как уже говорилось, производственная функция описывает техническую сторону производства. При этом все приведенные в разделах 1 и 2 соображения исходили из неизменности технического уровня производства: замена одного ресурса другим, изменение масштаба производства и т. д., - все эти изменения были переходами от одного производственного варианта к другому в пределах множества производственных возможностей, причем само это множество предполагалось неизменным; неизменной была и производственная функция.

В то же время в реальной жизни фирмы происходят изменения и другого рода: изобретаются новые материалы, старое оборудование заменяется более совершенным, работники приобретают новые знания и т. д. Кроме того, может совершенствоваться и продукция. Однако такие изменения мы здесь рассматривать не будем: теория предполагает, что продукт идеально однороден, тождествен самому себе, а усовершенствованный продукт - это уже другой продукт. Мы ограничимся рассмотрением только таких изменений в производстве, которые влияют лишь на затраты ресурсов и никак не сказываются на качестве продукта.

Как же производственная функция отражает такие изменения в производстве, которые характеризуются как технический прогресс?

Чтобы в дальнейшем избежать неясности, вначале исключим изменения, которые не относятся к техническому прогрессу. Допустим, что мы рассматриваем производственную функцию, имеющую своими аргументами всего два фактора - труд (L) и капитал (K). Одна из изоквант такой производственной функции показана на рисунке 36. Допустим, что фирма, оставаясь в пределах исходных технических возможностей, механизирует производство, увеличивая количество оборудования (т. е. Заложенного в производство капитала) и высвобождая некоторое количество труда; при этом она сохраняет прежний выпуск продукции. На рисунке 36 этому изменению соответствует переход по изокванте из точки А в точку В. Можно ли такое изменение считать проявлением технического прогресса? Разумеется, нет: мы остались в пределах прежних производственных возможностей, произошло лишь замещение одного ресурса другим.

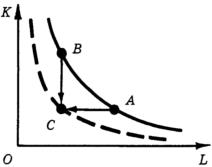
Рисунок 36 - Сдвиг изокванты производственной функции в результате технического прогресса

Ситуация была бы совершенно иной, если бы фирма, сохранив выпуск продукции, смогла бы уменьшить затраты труда без увеличения затрат капитала или, наоборот, смогла бы уменьшить затраты капитала без уменьшения затрат труда, т. е. смогла бы перейти из точки А или В в точку С, лежащую ниже и левее старой изокванты. В пределах исходных производственных возможностей такой переход не мог бы осуществиться: в точке С производственная функция принимала меньшее значение, чем на изокванте, проходящей через точки A и В. Значит, должна была измениться производственная функция. При этом изокванта, соответствующая исходному выпуску продукции, должна переместиться влево вниз и пройти через точку С.

Итак, технический прогресс - появление новых производственных возможностей. При этом прежние возможности не исчезают. Изобретение новых материалов не исключает использование традиционных. Так, внедрение капрона в качестве конструкционного материала в машиностроении не исключило применение стали - в каждом случае нужно выбирать более эффективный из имеющихся материалов. Получение новых знаний не означает немедленного забвения всего старого. Таким образом, технический прогресс означает расширение множества производственных возможностей. При этом варианты, которые в исходном множестве были технически эффективными, становятся неэффективными, и производственная функция должна учитывать новые эффективные варианты.

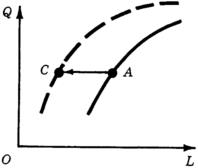
Рисунок 37 - Сдвиг графика производственной функции в результате технического прогресса

Изложенная здесь точка зрения на то, как изменения производственной функции отражают технический прогресс, получила широкое распространение и развитие. На ее основе разработаны показатели интенсивности технического прогресса; изменение наклона изоквант при их сдвиге позволяет классифицировать виды технического прогресса, различая трудосберегающее, капиталосберегающее, природосберегающее направления. Однако при этом возникает вопрос: почему определенная комбинация ресурсов "до прогресса" позволяла получить максимум 100 единиц продукта, а "после прогресса" та же самая комбинация тех же самых ресурсов позволяет получить, скажем, 120 единиц продукта? Если мы учли все используемые ресурсы и ничего не упустили, какая же сила породила дополнительные 20 единиц продукта?

На этот вопрос можно дать такой ответ: количество ресурсов осталось тем же самым, но изменилось их качество, так что "после прогресса" использованы не совсем те же самые ресурсы, которые были "до".

В долгосрочном периоде возможно изменение всех вводимых в производство ресурсов, как переменных, так и постоянных, но базовые технологии не изменяются. Применение всех видов ресурсов увеличивает масштабы производства, поэтому для анализа деятельности фирмы в долгосрочном периоде используют понятие отдачи от масштаба. При технически эффективном способе производства увеличение выпуска продукции обеспечивается за счет пропорционального увеличения использования всех производственных ресурсов. Это и есть изменение масштаба производства. Эффект роста масштабов производства может быть положительным (возрастающим), неизменным (постоянным) или отрицательным (убывающим), что характеризует масштаб деятельности фирмы.

Неизменный эффект масштаба производства означает, что удвоение использования всех факторов ведет к удвоению выпуска продукции. Это свидетельствует о том, что изменение масштаба деятельности фирмы не влияет на продуктивность используемых факторов производства.

Положительный эффект масштаба означает, что выпуск продукции увеличивается более чем в 2 раза. В этом случае выгоднее иметь крупное предприятие, производящее (при относительно низких издержках) продукции больше, чем мелкие фирмы с высоким уровнем издержек.

Убывающий эффект масштаба означает, что выпуск продукции не увеличивается более чем в 2 раза. Как правило, данный эффект обусловлен ограниченными возможностями управления крупным производством, нарушением координации потоков ресурсы—выпуск.

Во многих случаях характер отдачи от масштаба производства изменяется при достижении определенного уровня выпуска продукции, т. е. вначале действует постоянный или возрастающий эффект роста масштаба, а затем ему на смену приходит убывающий.

При прочих равных условиях чем больше эффект масштаба, тем более крупные фирмы функционируют в той или иной отрасли промышленности. Как правило, промышленные отрасли имеют больший эффект масштаба, чем отрасли сферы услуг, поскольку крупным фирмам требуются существенные капиталовложения в оборудование, чтобы они могли работать наиболее эффективно.

Изокоста – линия, демонстрирующая комбинации факторов производства, которые можно купить за одинаковую общую сумму денег. Изокосту иначе называют линией равных издержек. Изокосты являются параллельными прямыми, поскольку допускается, что фирма может приобрести любое желаемое количество факторов производства по неизменным ценам. Наклон изокосты выражает относительные цены факторов производства (Рисунок 38). На рисунке 36 каждая точка на линии изокосты характеризуется одними и теми же общими издержками. Эти линии прямые, поскольку факторные цены имеют отрицательный наклон и параллельны.

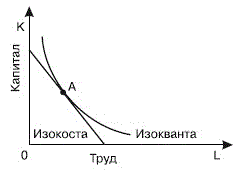
Рисунок 38 -Изокоста и изокванта

Совместив изокванты и изокосты, можно определить оптимальную позицию фирмы. Точка, в которой изокванта касается (но не пересекает) изокосты, означает наиболее дешевую по стоимости комбинацию факторов, необходимых для выпуска определенного объема продукта (Рисунок 36). На рисунке 36 показан метод определения точки, в которой минимизируются издержки производства заданного объема производства продукта. Эта точка расположена на самой нижней изокосте, где изокванта соприкасается с ней.

Равновесие производителя – состояние производства, при котором использование факторов производства позволяет получить максимальный объем продукции, т. е. когда изокванта занимает самую отдаленную от начала координат точку. Чтобы определить равновесие производителя, необходимо совместить карты изоквант с картой изокост. Максимальный объем выпуска будет в точке касания изокванты с изокостой (рис. 8).

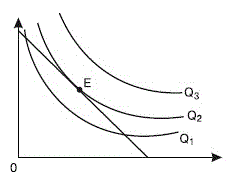
Рисунок 39 -Равновесие производителя

Из рисунка 39 видно, что изокванта, расположенная ближе к началу координат, дает меньшее количество производимой продукции (изокванта Q₁). Изокванты, расположенные выше и правее изокванты Q₂, вызовут изменение большего объема факторов производства, нежели позволяет бюджетное ограничение производителя.

Таким образом, точка касания изокванты и изокосты (на рисунке 37 точка Е) является оптимальной, поскольку в этом случае производитель получает максимальный результат.

Путем соединения точек касания изоквант и изокост, получают линию роста, или "путь развития" (Рисунок 40).

Расширение производства возможно различными путями. В коротком периоде мы можем увеличить объем применения лишь переменного фактора (Рисунок 41).

В длительном периоде расширение производства возможно по лучам ОА и 0В (Рисунок 42).

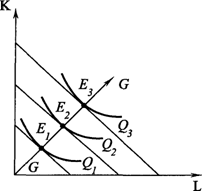
Рисунок 40 - Линия роста, или "путь развития"

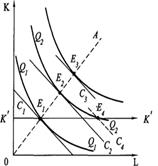Рисунок 41 - Линия роста фирмы в коротком периоде

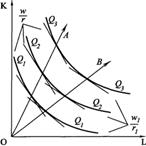Рисунок 42 - Расширение производства и линия роста в длительном периоде

Тема 4