ОПРЕДЕЛЕНИЕ ИНДУКТИВНОСТИ СОЛЕНОИДА
Цель работы - определение индуктивности соленоида по его сопротивлению переменному току.
Приборы и принадлежности: исследуемый соленоид, звуковой генератор, электронный осциллограф, миллиамперметр переменного тока, соединительные провода.
Явление самоиндукции. Индуктивность
Явление электромагнитной индукции наблюдается во всех случаях, когда изменяется магнитный поток, пронизывающий проводящий контур. В частности, если электрический ток течет в проводящем контуре, то он создает пронизывающий этот контур магнитный поток Ф.
При изменении силы тока I в любом контуре изменяется и магнитный поток Ф, вследствие этого в контуре возникает электродвижущая сила (ЭДС) индукции, которая вызывает дополнительный ток (рис. 1, где 1 - проводящий замкнутый контур, 2 - силовые линии магнитного поля, создаваемого током контура). Это явление называется самоиндукцией, а дополнительный ток, вызываемый ЭДС самоиндукции, – экстратокомсамоиндукции.
Явление самоиндукции наблюдается в любой замкнутой электрической цепи, в которой протекает элетрический ток, при замыкании или размыкании этой цепи.
Рассмотрим, от чего зависит величина ЭДС εs самоиндукции. Магнитный поток Ф, пронизывающий замкнутый проводящий контур, пропорционален магнитной индукции В магнитного поля, создаваемого током, протекающим в контуре, а индукция В пропорциональна силе тока.
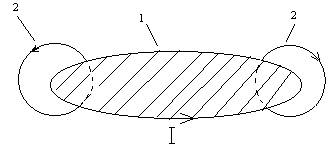
Рис. 1
Тогда магнитный поток Ф пропорционален силе тока, т.е.
Ф = L · I, (1)
где L - индуктивность контура, Гн (Генри).
Из (1) получим
L = Ф/I . (2)
Индуктивностью контура L называется скалярная физическая величина, равная отношению магнитного потока Ф, пронизывающего данный контур, к величине силы тока, текущего в контуре.
Генри - это индуктивность такого контура, в котором при силе тока в 1А возникает магнитный поток 1Вб, т.е. 1 Гн = 1 
.
Согласно закону электромагнитной индукции
. (3)
Подставляя (1) в (3), получим ЭДС самоиндукции:
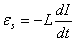. (4)
Формула (4) справедлива при L=const.
Опыт показывает, что при увеличении индуктивности L в электрической цепи сила тока в цепи увеличивается постепенно (см. рис. 2), а при уменьшении L сила тока уменьшается так же медленно (рис. 3).
Сила тока в электрической цепи при замыкании изменяется по закону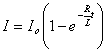 
, а при размыкании – по закону 
.
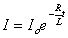Кривые изменения силы тока показаны на рис. 2 и 3.
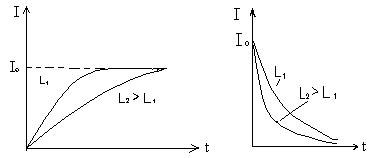
Рис. 2 Рис.3
Индуктивность контура зависит от формы, размеров и деформации контура, от магнитного состояния среды, в которой находится контур, а также от других факторов.
Найдем индуктивность соленоида. Соленоид - это цилиндрическая трубка, изготовленная из немагнитного непроводящего материала, на которую плотно, виток к витку, намотана тонкая металлическая проводящая проволока. На рис. 4 показан разрез соленоида вдоль цилиндрической трубки по диаметру (1 - силовые линии магнитного поля).
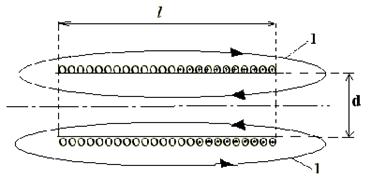
Рис. 4
Длина l соленоида намного больше, чем диаметр d, т.е.
l>> d. Если l< d, то соленоид можно рассматривать как короткую катушку.
Диаметр тонкой проволоки намного меньше, чем диаметр соленоида. Для увеличения индуктивности внутрь соленоида помещают ферромагнитный сердечник с магнитной проницаемостью μ. Если l>>d, то при протекании тока внутри соленоида возбуждается однородное магнитное поле, индукция которого определяется формулой
В=μо μnI, (5)
где μо = 4π·10-7 Гн/м – магнитная постоянная; n = N/l – число витков единицы длины соленоида; N – число витков соленоида.
Вне соленоида магнитное поле практически равно нулю. Поскольку соленоид имеет N витков, то полный магнитный поток ψ(потокосцепление), пронизывающий поперечное сечение S соленоида, равен
Ψ = NФ = NВS, (6)
где Ф = BS – поток, пронизывающий один виток соленоида.
Подставляя (5) в (6) и с учётом того, что N = nl, получим
Ψ = μо μn2 lSI . (7)
С другой стороны,
Ψ = LI . (8)
Сравнивая (7) и (8), получим
L = μо μn2 lS = μо μ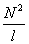 
S. (9)
Площадь сечения соленоида равна
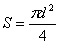. (10)
С учётом (10) формула (9) запишется в виде
L = μо μ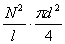 
. (11)
Определить индуктивность соленоида можно, подключив соленоид в электрическую цепь переменного тока с частотой ω. Тогда полное сопротивление (импеданс) определится формулой
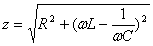, (12)
где R – активное сопротивление, Ом;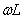 
= хL – индуктивное сопротивление; 
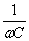= хс – ёмкостное сопротивление конденсатора с
ёмкостью С.
Если в электрической цепи отсутствует конденсатор, т.е. электроёмкость цепи мала, то хс<< хL и формула (12) будет иметь вид
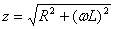. (13)
Тогда закон Ома для переменного тока запишется в виде
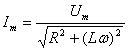, (14)
где Im , Um – амплитудные значения силы тока и напряжения.
Так как ω = 2πν, где ν – частота колебаний переменного тока, то (14) примет вид
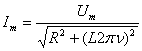. (15)
Из (15) получим рабочую формулу для определения индуктивности:
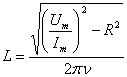. (16)
Дата добавления: 2016-01-29; просмотров: 1981;