Коэффициент самоиндукции.

Для количественного определения коэффициента самоиндукции некоторого контура мыможем воспользоваться любым из соотно­шений, характеризующих в той или иной степени электрокинетический процесс, протекающий в этом контуре. Действительно, в простейшем случае, когда мы имеем дело с одной, и только с одной, неизме­няемой цепью, мы имеем:

L=const

и можем написать, например, следующий ряд соотношений:

Основываясь на этом, мы получаем:

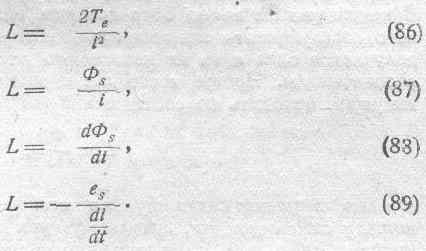
Все эти соотношения количественно совершенно равноценны и приводят к одному и тому же значению коэффициента самоиндук­ции. Однако, сказанное справедливо без всяких оговорок только для случая, когда в пространстве, окружающем проводник, отсутствует вещество, могущее принимать участие в том электромагнитном про­цессе, который происходит в поле потока самоиндукции. Другими словами, все сказанное справедливо для случая пустоты, для которой мы имеем:

m₀=const=1.

Наличие же вещества в пространстве, окружающем проводник, привносит в нашу систему, состоящую из одного явно выраженного проводящего контура, еще большое количество неявных электри­ческих цепей в форме элементарных электронных орбит, которые существуют, как мы теперь знаем, в каждом атоме вещества и ко­торые, по существу, должны быть учтены, когда мы выражаем электрокинетическую энергию системы и рассматриваем

общие электромагнитные условия. Итак, говоря об одном уединенном кон­туре электрической цепи, мы должны мыслить его в пустоте. Мы говорим в этом случае об истинном коэффициенте самоиндукции в отличие отдействующего коэффициента самоиндукции, с ко­торым мы обычно оперируем при наличии железа и других ферро­магнитных материалов в поле потока самоиндукции или о котором мы условно можем говорить при игнорировании других цепей, электромагнитно взаимодействующих с данной цепью. В случае, например, присутствия железа в поле тока, мы обычно не обращаем внимания на электромагнитные процессы, происходящие в самом веществе железа. Мы констатируем на опыте изменение индуктивных действий, которые наблюдаются в данной цепи, и упрощенно опи­сываем это явление, говоря, что коэффициент самоиндукции цепи изменяется благодаря наличию железа, т. е. принимаем, что дей­ствующий коэффициент самоиндукции некоторой цепи зависит от природы вещества (m), находящегося в поле тока. В дальнейшем (см. § 106) мы специально остановимся на вопросе о действующем коэффициенте самоиндукции. Мы покажем также, что величина действующего коэффициента самоиндукции может получаться, вообще говоря, разная, в зависимости от того, как мы его определяем. В настоящее же время сосредоточим внимание на величине истин­ного коэффициента самоиндукции, которая, как мы указали выше, получается одна и та же независимо от того, каким путем мы ее рассчитываем. Проще всего для определения коэффициента само­индукции исходить из соотношений (87) и (89). Первое дает:

L=Ф_s/i,

т.е. коэффициент самоиндукции некоторого контура численно равен потоку самоиндукции, сцепляющемуся с данным контурам, когда по нему идет ток, сила которого равна единице. Если мы будем иметь при

i=1 абс. эл.-магн. единице также и

Ф_s=1максвеллу,

то

L=1

в абсолютной электромагнитной системе единиц.

Величину практической электромагнитной единицы коэффициента самоиндукции, называемую генри, мл выведем из соотношения (89):

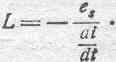
Если в этом отношении положим:

e_s=1 вольту

и

di/dt=1 амперу в секунду,

причем примем во внимание, что в некоторой определенной цепи е_s

и di/dt всегда бывают разных знаков, то получим:

L=1 генри,

т. е. коэффициентом самоиндукции, в один генри обладает такая неизменяемая цепь, в которой возникает электродвижущая сила самоиндукции, равная одному вольту, в то время как сила про­ходящего по ней тока равномерно возрастает или убывает со скоростью одного ампера в секунду.

Соотношение между генри и абсолютной электромагнитной еди­ницей коэффициента самоиндукции легко установить, приняв во внимание, что:

1 вольт=10⁸ абс. эл.-магн. единиц, 1 ампер=10^-1

На основании этого можем написать:

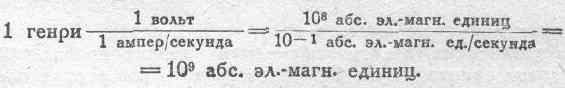
Связь между генри и абсолютной электромагнитной единицей коэффициента самоиндукции вытекает, конечно, и из соотношения (87), если исходить из практических единиц магнитного потока и силы тока. В таком случае можем написать:

т. е. то же, что было получено выше.

При вычислении величины коэффициента самоиндукции некоторого контура чаще всего пользуются соотношением (87):

L=Ф_s/i.

В связи с этим приходится путем расчета определять вели­чину Ф_s, которую мы иногда, ради ясности, будем называть полным потоком самоиндукции, сцепляющимся с данным контуром. Значение этого термина мы разъясним в нижеследующих строках. Вместе с тем заметим, что все, относящееся к вопросу о полном потоке

самоиндукции, может быть распространено на всякийвообще маг­нитный поток, сцепляющийся с некоторым контуром и играющий существенную роль при определении электродвижущих сил, которые могут индуктироваться в этом контуре. По существу во всех случаях электромагнитной индукции имеет первенствующее значение не вопрос о том, сколько именно максвеллов входит в состав рассма­триваемого магнитного потока, а то, сколько раз все магнитные линии, составляющие этот поток, пересекут данный контур в случае исчезновения потока. Другими словами, имеет значение число сцеплений данного реально существующего потока с рассматриваемым контуром. Числом сцеплений (полным потоком) мы будем называть число возможных пересечений проводящего контура магнитный потоком в случае исчезновения последнего.

Для простейшего рассмотренного случая, т. е. для электрической цепи, состоящей из одного витка (см. рис. 153), число сцеплений магнитного потока с контуром будет равно числу магнитных линий потока самоиндукции, определяемого силою проходящего по контуру тока. Назовем этот магнитный поток (измеряемый числом магнит­ных линий)—реально существующим магнитным потоком (Ф'_s) Итак, в случае цепи, состоящей из одного витка, соблюдается равенство между реально существующим потоком (Ф'_s) н числом сцеплений этого потока с витком (Ф_s) т. е. полным потоком самоиндукции:

Ф'_s=Ф_s.

Следует при этом иметь в виду, что в случае беспредельно тонкого проводника (практически — очень тонкого проводника) мы можем поток самоиндукции Ф_s рассматривать как распределенный полностью в пространстве, окружающем проводник. В случае же, когда диаметр проводника не настолько мал по сравнению с геоме­трическими размерами контура цепи, чтобы им можно было прене­бречь, и если при этом необходим более точный количественный учет явления, следует принимать во внимание и ту составляющую потока самоиндукции Ф_s, которая распределена в объеме самого провода. Это замечание полностью относится ко всякому, вообще говоря, потоку Ф, сцепляющемуся с некоторой цепью.

В сложных цепях, состоящих из нескольких витков, вышеука­занное равенство, вообще говоря, нарушается, т. е.:

Ф_s¹Ф,

так как одна и та же магнитная линия может сцепляться с несколь­кими витками, и, следовательно, полное число сцеплений данного магнитного потока с контуром или, иначе, полный поток самоиндукции может быть значительно, иногда во много раз, больше реально суще­ствующего потока. Таким образом, под полным магнитным потоком, сцепляющимся с некоторым сколь угодно сложным проводящим кон­туром, мы будем разуметь эквивалентный поток, который в одном простом витке может произвести такое же индуктивное действие,

как и данный реально существующий поток в рассматриваемом сложном контуре.

Поясним сказанное на примерах. При этом обратим внимание на следующее. Каждая магнитная линия представляет собою неко­торый вполне определенный замкнутый контур. Отдельные же витки сложного проводящего контура могут быть выражены недостаточно отчетливо. Поэтому, во избежание ошибок при опреде­лении числа сцеплений, пра­вильнее подсчитывать число проводников, проходящих сквозь контур каждой от­дельной магнитной линии или сквозь контур пучка тожде­ственных магнитных линий. Обратное, т. е. подсчет числа магнитных линий, пронизы­вающих каждый отдельный виток, не всегда выполнимо с достаточною точностью.

Допустим теперь, что про­ходящий по цепи ток i обу­словливает реально суще­ствующий магнитный поток в 6 линий, располагающихся, как показано на рис. 154.

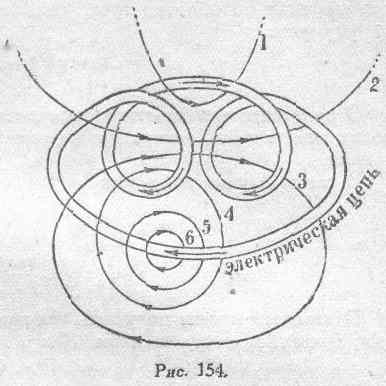
Магнитные линии 1-я, 5-я и 6-я имеют по одному сцеплению, 4-я — два сцепления, 2-я же и 3-я сцепляются с контуром по три раза.

Таким образом, реально существующий магнитный поток в данном случае состоит из 6 линий:

Ф'= 6,

тогда как полное число сцеплений магнит­ного потока с контуром или, что то же, полный магнитный поток, сцепляющийся с данным сложным контуром, выражается так:

Ф_з=1X3+2X1+3X2=11 максвеллов.

В качестве второго примера сложного контура рассмотрим тороид (рис. 155) с равномерно наложенной обмоткой, состоящей из n витков изолиро­ванной проволоки.

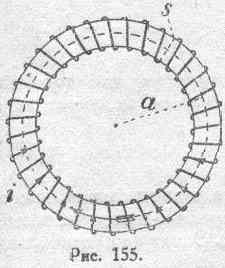
Длину средней линии этого тороида обозначим через l, причем:

l=2pа,

где а есть средний радиус тороида. Площадь поперечного сечения обозначим через s.

Допустим далее, что диаметр этого сечения очень мал сравни­тельно с диаметром тороида (2а). В связи с этим можем принять для всех точек внутри соленоида:

Н=const.

Реально существующий магнитный поток в этом случае, при прохождении по обмотке тока, сила которого есть /, определится

из формулы:

Ф'=Bs=mHs=ms(4pi/l).

В силу симметричности рассматриваемой системы и тождественности всех витков, можем предположить, что нет магнитного рас­сеяния.

В таком случае получаем:

Ф_s=Ф'n, т. е.

Ф_s=ms(4pi/l)n.

Отсюда мы можем получить величину коэффициента самоиндук­ции, пользуясь соотношением (87):

В случае пустоты, что именно по существу мы и имеем в виду при настоящем рассмотрении вопроса об истинном коэффициенте самоиндукции, можем положить:

m=m₀=1,

и численное значение коэффициента самоиндукции для тороида с равномерно распределенной обмоткой из n витков получает вид:

При расчете коэффициента самоиндукции в данном случае можно итти и другим путем. Рассчитаем, для примера, коэффициент само­индукции тороида, исходя из соотношения (86). Электрокинетическая энергия рассматриваемой цепи равна:

T_e=¹/₂Li².

Она представляет собою (см. § 21) энергию магнитного поля а пространстве вокруг проводника. В данном случае все магнитное поле потока самоиндукции сосредоточено внутри обмотки тороида в объеме sl, и потому вычисление энергии магнитного поля особенно просто. Действительно, как известно из главы о магнитном по-

токе (§ 21), энергия магнитного поля выражается следующим об­разом:

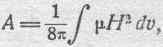
где mH²/8p— есть энергия магнитного поля в единице объема (в данном

случае внутри соленоида). Следовательно,

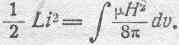
Интегрируя, получаем:

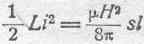
или

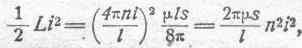
откуда

т. е. мы и этим путем расчета получили ту же величину L. Это лишний раз подтверждает, что коэффициент самоиндукции должен подсчитываться именно по числу сцеплений потока с контуром, а не по числу реально существующих магнитных линий.

Не следует думать, что полный поток самоиндукции или полное число сцеплений есть лишь некоторое геометрическое представление, фикция, не имеющая простого физического смысла. Наоборот, пол­ный поток самоиндукции есть как раз то реальное

„количество движения в электрокинетическом процессе”, которое определяет собою все интересующие нас электромагнитные процессы в системе. В самом деле, когда мы рассматриваем процесс индуктирования электродвижущей силы в проводнике, то величину ее мы должны рассчитывать, как было подчеркнуто выше, не по числу магнитных линий, существующих в пространстве, а по числу пересечений этих линий проводником, так как именно число пересечений определяет число отпочковывающихся свободных магнитных звеньев в случае возникновения индуктированного тока. С другой стороны, когда мы рассчитываем величину потока, обусловливаемого электрическим током, то принимаем во внимание число ампервитков, а не просто силу тока. Один и тот же ток может создать различной величины поток и при этом обусловить различной величины противодействие создающей ток электродвижущей силе, в зависимости от числа витков, т. е. от числа сцеплений.

Вообще говоря, коэффициент самоиндукции некоторого проводника определенной длины не есть величина постоянная, но зависит от формы, которая ему придана. Это явно следует из того, что коэффициент самоиндукции есть функция геометрических координат.

В случае, например, проводника в виде спирали (рис. 156) коэф­фициент самоиндукции будет в значительной степени зависеть от того, насколько сближены отдельные витки между собою.

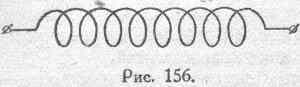
Наиболь­шее значение L такой спирали будет достигнуто при тесном сбли­жении витков, так как при этом будут наиболее благоприятные условия для того, чтобы реально существующий поток самоиндук­ции имел возможно большее число сцеплений с рассматриваемым контуром. Раздвигая витки, мы будем уменьшать L и, вытянув проводник в прямую линию, достигнем некоторого предела. Можно итти дальше в отношении уменьшения коэффициента самоиндукции данного проводника, что на практике нередко требуется. С этою целью необходимо перегнуть проводник пополам (рис. 157) и обе половины сблизить в возможно большей степени, насколько это позволяет толщина изоляции.

Так как при этом весь поток самоиндукции должен охватываться обра­зовавшейся петлей, площадь которой при достаточно тон­ком слое изоляции может быть очень мала, то ясно, что и величина потока самоиндукции при данной силе тока будет весьма незначительна. Теоретически поток само­индукции Ф_s в этом случае может быть сколь угодно мал. Из этого следует, что коэффициент самоиндукции некото­рого проводника определенной длины может быть приведен к очень малому значению пу­тем складывания проводника вдвое, т. е. путем образова­ния так называемого бифиляра. Такой, вдвое сложенный, проводник может быть сколь угодно большой длины. Его далее обычно наматывают на катушку и получают бифилярную обмотку, состоящую из двух совме­щаемых систем витков, по которым протекает ток в противо­положных направлениях. Благодаря этому катушка с бифилярной обмоткой не может обладать потоком самоиндукции, пронизываю­щим все витки катушки подобно тому, как это имеет место в случае обычной катушки с ординарной обмоткой. Вместе с тем коэффи­циент самоиндукции бифилярной обмотки ничтожно мал и опреде­ляется только местными магнитными потоками в промежутках между соседними витками, по которым протекают электрические токи противоположного направления.

Однако, следует помнить, что, изменяя коэффициент самоиндукции цепи путем изменения формы и размеров этой цепи, мы не можем сделать его равным нулю. В самом деле, на основании равенства:

Ф_s=Li

можно утверждать, что если бы мы имели:

L=0,

то и

Ф_s=0,

т. е. при наличии в контуре электрического тока магнитный поток связанный с контуром, отсутствовал бы, и мы имели бы случай тока без магнитного потока. Но мы знаем, что наличие магнитного потока вокруг контура тока есть единственный совершенно неотъ­емлемый признак существования электрического тока. Кроме того, здесь мы имеем полную аналогию с механической системой. Коэф­фициент самоиндукции L, характеризующий собою электромагнитную инерцию системы, соответствует в механической системе коэффи­циенту инерции, в частном случае массе m. И подобно тому, как мы не мыслим никакой материальной системы, не обладающей массой, так же принципиально невозможно представить себе и элек­трическую цепь, не обладающую электромагнитной инерцией, т. е. некоторым определенным коэффициентом самоиндукции, хотя бы и сколь угодно малым. Тем более коэффициент самоиндукции не может быть отрицательной величиной. Всегда принципиально:

L>0.

Это очевидно как из определения L, как коэффициента электро­магнитной инерции, ибо отрицательная величина L соответствовала бы „отрицательной массе", так и из того же соотношения:

L=Ф_s/i.

Так как ток и поток самоиндукции, с ним связанный, всегда одного знака (правило штопора), то коэффициент самоиндукции всегда есть принципиально положительная величина.

Утверждение, что коэффициент самоиндукции L никогда не может быть равен нулю, ни в малейшей степени не противоречит тому, что в цепях постоянного тока не приходится сталкиваться, при установившемся режиме, с проявлениями самоиндукции. Совер­шенно очевидно, что в цепи постоянного тока с установившимся режимом имеет место не отсутствие электромагнитной инерции, а лишь отсутствие ЭДС самоиндукции. ЭДС самоиндукции, вычис­ляемая согласно соотношению:

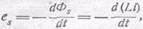
может иметь место только в случае, когда i или L—величины пере­менные. В случае же жесткой цепи с постоянным током (L=const и i=const) будем иметь:

e_s=0.

В случаях же, когда или i¹const, или L¹const, ЭДС само­индукции совершенно явственно обнаруживается. Первое (i¹const) имеет место в моменты замыкания и размыкания цепи постоянного тока, второе (L¹const) — при всяком изменении конфигурации цепи.

Итак, всякая цепь безусловно обладает коэффициентом самоин­дукции L¹0, независимо от характера тока. Но это свойство всякой

цепи незаметно при постоянной силе тока, совершенно так же, как инерция материального тела неощутима, когда тело находится в покое или движется прямолинейно и равномерно.