Информативность результатов пассивного производственного эксперимента

Производственный процесс можно рассматривать как определен­ную систему большого числа разнообразных входных и выходных параметров, анализ изменения значений (колебаний) которых и составляет сущность проведения пассивного эксперимента. Для анализа производственного процесса последовательность технологических операций удобно представлять в виде схемы ве­роятностного процесса перехода от одной операции к другой (рис. 7.1).

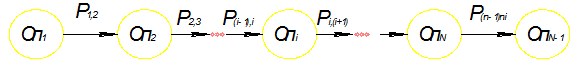
Рис. 7.1. Вероятностная схема представления технологического процесса

Система вероятностного перехода от одной операции к другой позволяет выявить наиболее критичные (с точ­ки зрения дефектности) технологические операции и на основании анализа дефектов на этих операциях принять меры к повышению их качества, а значит, и процента выхода годных изделий на этих операциях. Величина вероятности (р₁₂, р₂₃,..., р_(п-1)п) перехода от одной технологической операции (Оп₁, Оп₂,..., Оп_n-1) к другой определяет­ся экспериментально, как отношение числа годных изделий на выходе i-й технологической операции к общему числу изделий, по­ступивших на вход i-йоперации. Таким образом, анализ производственного процесса может производиться лишь в том случае, если задано требуемое значение функции отклика на i-й операции y_ТР, имеется его замерен­ное фактическое значение у_{i факт}, а также известны управляемые факторы Xi i-и технологической операции, при изменении значе­ний которых можно получить необходимое значение у_{i факт}.

Аналогично можно формализовать и процесс контроля. Сущ­ность его сводится к измерению фактических значений функций отклика или факторов x_{i факт}, сравнению их с требуемым значе­нием Х_{i тр}, оценке допустимости отклонений х_{i факт} - X_{i tp} = Δx. При этом на каждый контролируемый параметр, например Xi, уста­навливается допуск ε, чтобы отклонения фактических значений от требуемых значений находились в пределах допуска ± ε, т. е.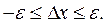

Применяя статистический анализ интересующих исследователя параметров процесса на конкретных технологических операциях, можно получить распределение этих параметров после конечной операции. При этом часто распределения выходных парамет­ров на каждой технологической операции, являются параметрами готового изделия и характеризуют его качество. Эти параметры качества несут наиболее интересную информацию о технологическом процессе при проведении пассивного эксперимента в производственных условиях.

В любом процессе возникают погрешности, из-за которых значения параметров качества изделий могут отличаются от требуемых. Такие разнообразные по своей природе и значимости производственные погрешности разделяют на три вида:

- случайные погрешности, появление которых мож­но предсказать только с некоторой вероятностью. При этом ни ве­личину, ни знак отклонения параметров качества от номинала невозможно предсказать с полной определенностью;

- систематические погрешности можно предсказать точно. Систематические погрешности обычно делятся на постоянные и за­кономерно изменяющиеся;

- грубые ошибки («промахи»), зависящие от ошибок операторов, неправильно рассчитанных технологических режимов и т. д.

В производстве все погрешности проявляются в совокупности и вызываются в основном следующими факторами:

- погрешностями в работе технологического оборудования, обус­ловленными дефектами электрических, механических и оптических узлов установок;

- погрешностями инструмента, обусловленными его износом, от­клонениями от требуемой конфигурации; эти факторы часто явля­ются причиной, вызывающей закономерно изменяющиеся во вре­мени производственные погрешности;

- неточностью приспособлений и технологической оснастки, обус­ловленной в основном недостаточной их жесткостью, нарушением конфигурации и размеров, неправильной установкой в оборудова­нии и т. д.;

- неоднородностью электрофизических, механических и прочих свойств материалов и заготовок изделий;

- субъективными ошибками оператора

- метрологическими ошибками

Погрешности параметров качества технологического процесса и, в конечном итоге, его продукта и стабильность этих параметров - один из главнейших критериев качества процесса. Аналитическое или графическое описание взаимодействия (или взаимного влияния) технологических факторов производства и па­раметров качества изделий представляет собой, как правило, сто­хастическую модель технологического процесса, так как описы­вает статистическую связь между ними. Эта модель может использоваться для решения широкого круга технико-экономических проблем, например:

- оценки точности технологии в целом и на от­дельных операциях;

- оценки стабильности (или устойчивости) технологического про­цесса;

- выявления степени и характера влияния различных факторов на точность параметров качества и стабильность технологических процессов изготовления изделий;

- расчета и технико-экономического обоснования межоперацион­ных допусков на параметры качества изделий;

- выявления рационального уровня настройки и стабильности работы технологического оборудования, инструмента, оснастки и получения объективных данных для их модернизации и проекти­рования новых образцов;

- получения данных для оптимизации технологических процес­сов по их математическим и физическим моделям.

Планирование эксперимента и методы оптимизации параметров процесса

Основной целью проведения современного эксперимента с по­зиций производителя продукции является разработка математиче­ской модели, адекватно описывающей процесс и позволяющий, в конечном результате, осуществлять его управление. Именно с помощью такой модели можно эффективно управлять производ­ством, оперативно изменяя его параметры в соответствии с запро­сами потребителя и обеспечивая выпуск высококачественной про­дукции.

При этом исследователь должен:

1) обеспечить высокую надежность и четкость интерпретации результатов экспериментальных исследований;

2) составить четкую и последовательную логическую схему по­строения всего процесса исследования: что, когда и как нужно делать;

3) максимально формализовать процесс разработки модели и сопоставления экспериментальных данных различных опытов од­ного и того же объекта исследований с целью широкого примене­ния электронно-вычислительных средств.

Всем перечисленным требованиям отвечают статистические ме­тоды планирования эксперимента, являющиеся одним из эмпири­ческих способов математического описания и оптимизации сложных процессов. Начало математическому планированию экспериментов положено в 30-40-х годах.

При планировании эксперимента рассматриваются только та­кие объекты, для которых выполняются требования воспроизводи­мостии управляемости. Первое требование означает, что при повторении эксперимента при одних и тех же значениях входных параметров результаты эксперимента имеют разброс, не превышающий некоторой заранее заданной величины (т. е. требо­ваний к точности эксперимента). Второе требование означает, что объект исследования должен быть управляемым, т.е. эксперимен­т - актив­ным.

Планирование эксперимента состоит в процедуре выбора чис­ла и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью. При этом обеспечивается следующее:

• одновременное варьирование всеми переменными по специ­альным правилам;

• использование математического аппарата, формализующего многие действия экспериментатора;

• выбор четкой стратегии, позволяющей принимать обосно­ванные решения после каждой серии экспериментов;

• минимизация общего числа опытов.

Наиболее часто требуется установить количественную связь между значением выходного параметра и факторами, от которых он зависит. Такой эксперимент называется интерполяционным.

В этом случае для описания объекта исследования удобно пользоваться кибернетической схематиза­цией, представляющей объект исследования в виде «черного ящика» (рис. 14.1). Стрелки справа, обозначенные у_ь изображают функции, результаты процесса характеристики целей исследования, т.е. «параметров оп­тимизации». Встречаются и другие названия: «критерий оптимиза­ции», «целевая функция», «выход черного ящика», «функция отклика»или просто «отклик» и т.д. Все способы такого воздействия на объект исследования (входы «черного ящика») обозначены х_i, и называются «факторами», «независимыми переменными». Совокупность возможных значений всех факторов можно рассматривать как k-мерное «факторное пространство» с координатами ( ).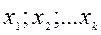

Для решения задачи необходимо создать математическое описание процесса, то есть математические модели, связывающие параметр оптимизации с факторами обычно представ­ляется в виде полинома, где У - функция отклика, а Х₁, Х₂, Хз,..., Хн- факторы исследуемого процесса. Процесс проверки степени соответствия математической модели описываемому процессу называют «проверкой адекватности», а полученную модель - «адекватной».

Каждый фактор может принимать в опыте одно из нескольких значений. Эти значения называют «уровнями». Всякий фактор имеет определенное число дискретных уровней. Фиксированный набор уровней факторов (т.е. установление каждого фактора на некото­рый уровень) определяет одно из возможных состояний «черного ящика». Одновременно это есть условия проведения одного из возможных опытов. Перебор всех возможных наборов состояний дает полное множество различных состояний данного «ящика», т. е. число возможных различных опытов. Число различных состоя­ний получается путем возведения числа уровней факторов в сте­пень числа факторов k.

Выбор параметра оптимизацииопределяется тем аспектом, который в конкретном случае представляет наибольший интерес.

Параметры оптимизации могут быть весьма разнообразными:

- экономические: прибыль, себестоимость, рентабельность и т.п.;

- технико-экономические: производительность, эффективность, долговечность, надежность и т.п.;

- статистические: характеристика распределения, дисперсия, стандартное отклонение;

- чисто технические: размер, характеристика механических свойств и т.п. При механической обработке могут выбираться такие параметры оптимиза­ции, как стойкость режущего инструмента, точность базирова­ния, точность обработанных поверхностей, шероховатость поверх­ности детали и т. п.

Параметр опти­мизации должен удовлетворять следующим требованиям.

1. Быть количественным, т. е. всегда задаваться числом. То множество значений, которые может принимать пара­метр оптимизации, называется областью определения. Если нет способа измерения параметра оптимизации или он не может быть количественно зафиксирован, необходимо провести его ранжирова­ние, то есть присвоение рангов по зара­нее выбранной шкале.

2. Быть однозначным в статистическом смысле,т. е. заданному набору значений факто­ров должно соответствовать с точностью до ошибки эксперимен­та определенное значение параметра оптимизации.

3. Быть простым, иметь физический смысл, лег­ко вычисляться и выражаться одним числом.

4. Оценивать действительную эффективность функцио­нирования системы или качество объекта, т.е. задача эксперимента должна ставиться корректно.

5. Обладать по возможности универсаль­ностью и полнотой, то есть всесторонне характеризовать объект исследования, что выполняется далеко не всегда. Например, часто характеристики качества вступают в противоречие с экономическими ас­пектами.

Выбор факторов играет важнейшую роль в построении математической модели, см. § 3.4

Если какой-либо существенный фактор окажется не включенным в совокуп­ность управляемых исследователем условий проведения экспери­ментов, и при этом его уровень не будет контролироваться, то это может привести к значительным погрешностям результатов. Если неучтенный фактор произвольно принимал случайные значения, а информация об этом не была зафиксирована, это также значительно увеличит ошибку опыта. При поддержании фактора на некотором фиксированном уровне (не задействован в эксперименте) может быть получено лож­ное представление об оптимуме, так как при другом фиксированном уровне этого фактора оптимум параметра оптимизации может сместиться.

При планировании эксперимента факторы должны быть уп­равляемыми (активный эксперимент). Нужно знать последователь­ность действий (операций), с помощью которых устанавливаются конкретные значения (уровни) фактора («операциональный» фактор).

Дополнительные требования предъявляются к совокупности факторов:

1. Требованиесовместности: все комбинации факторов должны быть осуществимы и безопасны. Если это требование не выполняется,необходимо разбить область определения факторов на диапазоны, «блоки».

2. Требование независимости, «некоррелированности», «ортогональности» факторов. При существенной связи между рассматриваемыми факторами (явление «мультиколлинеарности») не удаётся получить достоверной математической модели

Методология планирования эксперимента

Ещё перед планированием эксперимента в области, содержащей экстремум параметра оптимизации, когда ещё нет достаточной априорной ин­формации, иссле­дователь должен хотя бы приблизительно представлять форму поверхности отклика, чтобы «добраться» до этой области экстремума. Поэтому часто процедура планирования эксперимента проводит­ся в два этапа.

Первый этап - поисковый, «предпланирование» эксперимента нахождение области экстремума и получение качественного представления о форме поверхности отклика. На этом этапе обычно выбирают достаточно узкие пределы варьирования факторов, что позволяет адекватно отразить поверхность отклика в этих пределах линейной моделью.

Второй этап проводят для последующей более аргументированной «интерпретации модели», выбора модели, наиболее точно описывающей поверхность отклика в области экстремума.

Для наглядности рассмотрим поверхность отклика для эксперимента с двумя факто­рами. По одной оси координат будем откладывать в некотором масштабе значения (уровни) одного фактора, а по другой оси — второго, а по третьей - значения отклика. В этом случае поверхность отклика Б в факторном пространстве будет выглядеть так, как это показано на рис. 14.2.

Рис. 14.2. Графическое представление поверхности отклика в факторном пространстве [19]

Для двух факторов наглядное представление о поверхности отклика можно получить путем её сечения плоскостями, параллельны­ми плоскости Х₁Х₂ и проецирования полученных в сечениях линий на эту плоскость. Получаются так называемые линии равных уровней, или, в нашем случае, линии равного отклика,каждая из которых соответствует постоянному значению параметра оптимизации.

В силу того что невозможно измерить отклик при каждом сочетании факторов, необходимо выбрать такую стратегию, которая приближала бы к оптимуму. Для этого используется так называемый шаговый принцип предпланирования эксперимента. Предположим, что опти­мум существует и что поверхность отклика непрерывная, гладкая и имеет единственный оптимум. В большинстве случаев в области резания, металлорежущих станков и инструментов, в технологии машиностроения такое предположение, как показывает практи­ка, справедливо. А если это так, то можно представить изучаемую функцию в аналитическом виде.

Варианты шагового принципа предпланированияэксперимента представлены ниже, см. …4.4.

Построение интерполяционной моделиявляется завершающим, этапом планирования в области экстре­мума. Как правило, необходимо последовательно повышать сте­пень полинома и рассчитывать коэффициенты модели до тех пор, пока не будет достигнута её адекватность. Поэтому в планирова­нии эксперимента общепринята такая процедура: вначале выби­рают простейшую модель (обычно линейную, т.е. модель первого порядка) и находят для нее коэффициенты. Подставляют в эту модель значения параметров и рассчитывают отклик у. Затем по специальным формулам статистики проводят оценку адекватнос­ти модели (формулы рассматриваются далее). Если адекватность доказана, то эксперимент считают завершенным. Если же адек­ватности нет, берут следующий по порядку полином и снова пос­ле расчетов оценивают адекватность. Увеличение порядка поли­нома проводят до тех пор, пока не будет достигнута адекватность модели или, если число членов в усложненной полиномиальной модели превышает число экспериментов, проводят дополнитель­ные эксперименты. В некоторых случаях, если проведение самих экспериментов не связано с большими расходами, а бблыпую часть расходов составляет подготовка условий для проведения экспери­ментов, поступают в обратном порядке. Проводят избыточное число экспериментов, берут за основу модель высокого порядка и вы­полняют расчеты коэффициентов модели и оценку адекватности, поэтапно упрощая модель до тех пор, пока не будет достигнут предел точности получения экспериментальных данных.

Для описанной процедуры рекомендуется выбирать модель в виде степенных функций следующего вида (такого типа функции часто применяют при исследовании процессов резания):

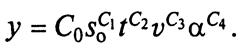
Приведенную модель иногда записывают в логарифмическом виде:

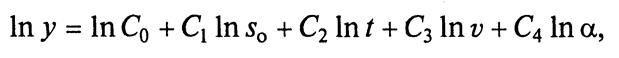
а после вычислений производят потенцирование. Это позволяет при расчете коэффициентов модели использовать приемы расчета, от­работанные для полиномов. С помощью специальных формул, о которых будет идти речь далее, по результатам экспериментов рас­считывают постоянные коэффициенты С_о, С_ь С_ъ С₃ и С₄.

Очень удобным видом модели являются полиномиальные моде­ли, которые позволяют выявить влияние на параметр оптимиза­ции не только отдельных факторов, но и их взаимодействие. По­линомиальные модели именуются по наибольшей степени факто­ра в полиноме:

• модель нулевой степени у = й0;

• первой степени у = Ьо + Ьхх{ + Ъ2х2\

• второй степени у = 60 + Ьххх + Ь2х2 + ЬХ2ххх2 + Ъхххх + Ъ22х\\

• третьей степени у - Ьо + Ьххх + Ь2х2 + ЬХ2ххх2 + Ьхххх + Ь22х2 + + ЬХХ2х\х2 + bmxxxl + Ътх\ + Ь222х2\

Чем сложнее функция отклика, тем более высокий порядок полинома приходится использовать для достижения требуемой точности математического описания исследуемого процесса. Как правило, функция отклика нам неизвестна, но мы предполагаем (на основе теории, литературных данных, но лучше всего — на основе проведенных однофакторных экспериментов), что ее при­ближенно можно описать одной из представленных выше формул. Операция замены неизвестной функции по некоторой совокуп­ности экспериментальных откликов другой функцией, условно говоря, эквивалентной, называется аппроксимацией, т.е. мы апп­роксимируем неизвестную функцию полиномом. На рис. 14.7 пред­ставлен пример уменьшения погрешности аппроксимации экспе­риментальных данных по мере увеличения порядка полиномиаль­ной модели. Как видим, чем больше членов в полиномиальной модели, тем более точно она отражает экспериментальные ре­зультаты. Однако, как будет показано в дальнейшем изложении, с увеличением числа членов необходимо провести большее число экспериментов, чтобы найти значения коэффициентов.

Необходимо отметить еще одно обстоятельство. Как ни стран­но на первый взгляд это звучит, существует понятие «чрезмерной (или неоправданной) точности». Дело заключается в том, что при любом экспериментальном исследовании есть некоторая ошибка

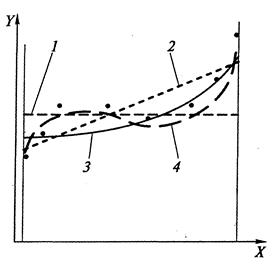
Рис. 14.7. Примеры аппроксимации экспериментальных точек (•) по­линомами нулевого (i), перво­го (2), второго (3) и третьего (4) порядков [19]

Выделим основные этапы планированияэксперимента в области экстремума:

- выбор вида математической модели, которую планируется получить в результате эксперимента;

- разработка плана эксперимента, порядка проведения опытов, числа дублей,

- собственно эксперимент (отработка методики экспериментирования, оценка погрешностей, реализация плана опытов, оценка достоверности опытов).

- обработка результатов наблюдений, построение модели, анализ, обобщение, при необходимости планированиеэксперимента для совершенствования модели.

План эксперимента в этом случае определяет расположение экспериментальных точек в k-мерном факторном пространстве или, другими словами, условия для всех опытов, которые необходимо провести. Обычно план эксперимента задается в виде матрицы планирования, каждая строка которой определяет условия опыта, а каждый столбец - значения контролируемых и управляемых па­раметров в исследуемом процессе, т. е. значения факторов, соот­ветствующих условию опыта.

В последний столбец матрицы заносят значения функции от­клика у полученные экспериментальным путем в каждом опы­те, проведенным в соответствии с условиями, указанными в стро­ках матрицы планирования эксперимента.

Планирование эксперимента начинают с выбора центра плана, т. е. точки, соответствующей начальному значению всех исполь­зуемых в эксперименте факторов (х₁₀, х₂₀, х_k0) в окрестностях которой в дальнейшем ставится серия планируемых опытов. Очевидно, что начальным значениям факторов будет также соответ­ствовать начальное значение функции отклика у₀. Центр плана обычно выбирается на основе априорных сведений о процессе. Если же их нет, то обычно в качестве центра плана принимается центр исследуемой области.

Значение факторов в каждом опыте, в случае применения ма­трицы планирования эксперимента, отличается от начального их значения x_i0 на величину интервала варьирования ΔХ_i. Одним из важнейших предварительных условий успешного проведения эксперимента с целью разработки математической модели, адекватной исследуе­мому процессу, является выбор оптимальной величины интервала ΔХ_i.

Предположим, что исследуемая функция Y=f(X₁) имеет вид, приведенный на рис. 4.1. Если выбрать ΔХ₁ неболь­шим (ΔХ₁'), то при анализе результатов эксперимента можно придти к. ошибочному выводу о том, что его влиянием на функцию отклика можно пренебречь и при дальнейшем проведении эксперимента - исключить. Интервалы варьирования по каждому фактору ("управляемой" или "независимой" переменной Х_i) должны выбираться настолько большими, чтобы приращение величины выходного параметра (функции отклика) Y к базовому значению у₀ можно было бы надежно выделить на фоне «шума», создаваемого исследуемым процессом, при небольшом числе параллельных опытов. На рис. на примере линейной зависимости функции отклика Y от одного фактора Х₁ показано, что с увеличением интервала варьирования ΔХ₁ увеличивается "зона неопределённости"

книга?

, но одновременна увеличивается приращение функции Y.

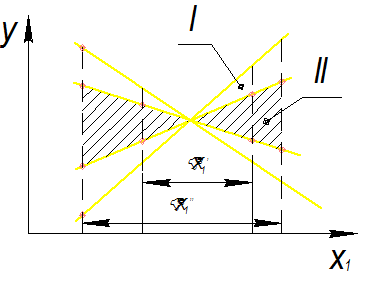
Рис. 4.4. Влияние размера интервала варьирования на точность определения зависимости Y=f (X) [20]

Но при увеличении ΔХ_i увеличивается другая опасность - получе­ние неадекватной модели. Так выбор слишком большой величины интервала варьирования (ΔХ"₁)приводит к необходимо­сти замены нелинейной модели линейной, см. рис. .

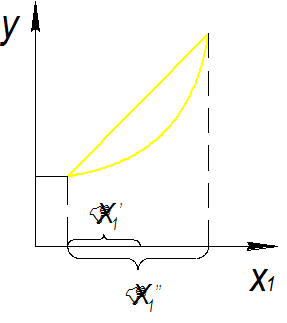
Рис. 4.1. Вид исследуемой функции (кривая 1) и два варианта выбора шага экс­перимента: ΔXi - заниженная величина; ΔXi" - завышенная величина [20]

Правильный выбор оптимальной величины интервала варьирования зависит от уровня знаний экспериментатором исследуемого процесса. При недостатке таких знаний руководствуются правилом, что интервал варьирования должен быть в пределах 0,05... ... 0,3 от диапазона варьирования исследуемого фактора.

Для удобства обработки результатов опытов, проводится преобра­зование текущих значений учитываемых в экспе­рименте факторов (x_i) к безразмерным величинам (x_iб= )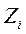

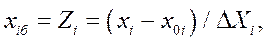(4.1)

где Xoi - базовое или начальное значение i-го фактора в центре плана; ΔX_i - значение интервала варьирования по i-му фактору; x_i - текущее значение i-го фактора.

Значения каждого фактора, которые принимаются для постановки опытов, называются уровнями варьирования данного фактора. Верхний уровень варьирования 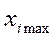в кодированном (безразмерном) виде всегда будет обозначаться Z = +1; нижний уровень варьирования 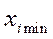в кодированном виде будет обозначаться Z = -1; нулевой уровень, то есть середина области варьирования ( 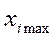+ 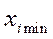)/2 будет обозначаться Z = 0. Таким образом, в кодированной системе значения факторов находятся в пределах: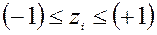

Например, пусть базовое значение одного из факторов исследуемого процесса равно Х = 400 ед. При этом шаг варьирования по этому фактору ΔX = 50 ед. Пусть варьирование значений фактора относительно его базового значения проводится на двух уровнях: X_max= 450 ед, X_min= 350 ед. Переходя от абсолютных значений рассматриваемого фактора к безразмерным его значениям, получим в соответствии с (4.1) для верхнего уровня рассматриваемого фактора Z_max= (450 - 400)/50 = + 1, а для нижнего - Z_min = (350 - 400)/50= -1. Координаты центра плана равны нулю и совпадают с началом координат. При составлении матрицы планирования эксперимента верхний и нижний уровни переменных для упроще­ния записи заменяют символами (+) и (-).

Непременным условием правильного построения модели является её гомоскедастичность (однородность дисперсий y_i в различных точках плана). Проверку гомоскедастичности проводят на основе критериев Кохрана, Бартлетта и им подобных, см. 3.3 на этапе первоначальной обработки результатов или предполагают её наличие на основе априорных сведений.

Разработку модели процесса обычно проводят по принципу «от простого к более сложному», то есть, если нет иных априорных представлений, начинают с предположения, что имитируемая модель исследуемого процесса является линейной и имеет вид полинома 1-го порядка.

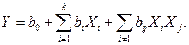(4.2)

Если после обработки и анализа результатов эксперимента выяснится, что сделанное предположение о линейности модели является ошибочным, переходят к планированию эксперимента из предположения, что эта модель может быть представлена полино­мом 2-го порядка и т. д. до тех пор, пока не будет разработана модель адекватная исследуемому процессу.