Опции программы MS EXCEL, предназначенные для регрессионного анализа

3.4.3.1 Использование инструмента анализа «Регрессия»

В пакете «Анализ данных» инструмент «Регрессия» (рис. 4.3) предлагает ли­нейный регрессионный анализ, который заключается в подборе графика для набора наблюдений с помощью метода наименьших квадратов. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или более (до 16) независимых переменных. То есть во «Входной интервал X» (рис. 4.3) можно вводить до 16 диапазонов. (Диапазоны обязательно должны быть представлены в столбцах.)Во«Входной интервал Y» вводят один диапазон, состоящий из одного столбца.

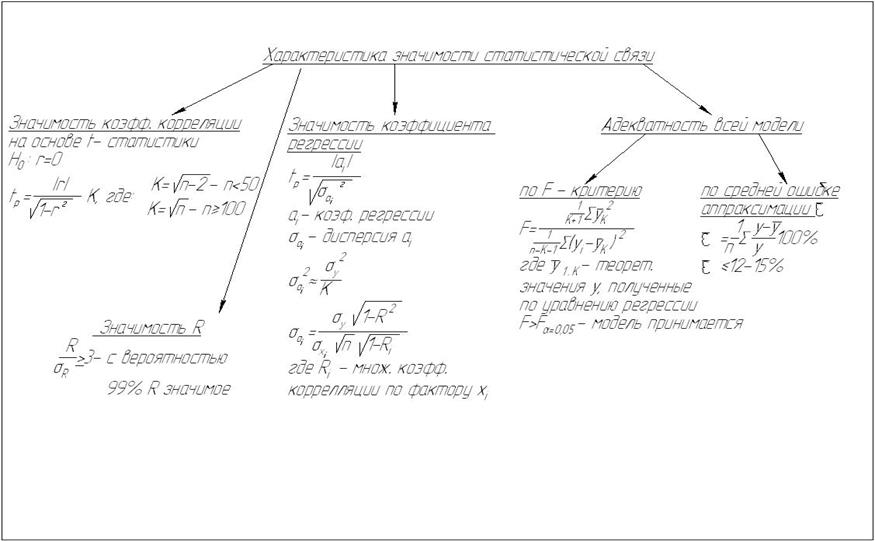
Рис. 4.2. Характеристики достоверности статистической связи

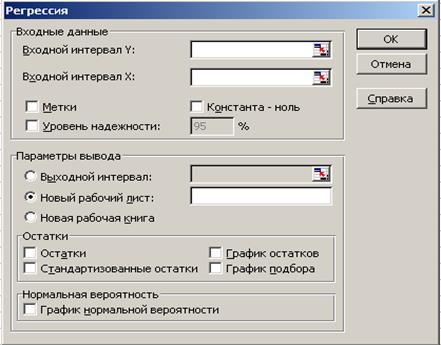
Рис. 4.3. Диалоговое окно инструмента анализа «Регрессия»

При желании получения уравнения регрессии без свободного члена (чтобы линия регрессии прошла через начало координат) следует в опцию «Константа - ноль» поставить «галочку». «Галочки» в опции «Остатки», «График остатков», «График подбора» или «Стандартизированные остатки» устанавливаются при необходимости исследования несоответствий между экспериментальными и теоретическими значениями Y, определяемыми уравнением регрессии. «Остаток» представляет собой разницу между фактическим и теоретическим значениями Y. «Стандартизированный остаток» представляет собой отношение «остатка» к «стандартной ошибке единичного наблюдения регрессионной статистики» (см. ниже). «График остатков» располагается в координатах x - величина остатка. По нему наглядно видны значения «остатка» для разных аргументов, что позволяет обнаружить «выбросы» - самые большие отклонения от теоретической модели, которые могут свидетельствовать о каком-то сбое, ошибке в получении результата. Процедура устранения таких «выбросов» называется «цензурированием».

На «графике подбора» в координатах x - Y показываются фактические и «предсказанные» данной регрессионной моделью значения Y.

Опция «График нормальной вероятности» позволяет в соответствии с появляющейся таблицей «ВЫВОД ВЕРОЯТНОСТИ» построить диаграмму в координатах «Персентиль выборки» - Y. То есть полученные значения Y в данном случае представлены в виде ранжированного вариационного ряда.

Результаты регрессионного анализа представляются как минимум (если не включены дополнительно отмеченные выше опции) в виде трёх таблиц.

1. Таблица «Регрессионная статистика» включает в себя рассчитанные значения следующих показателей:

- множественного коэффициента корреляции («Множественный R»);

- квадрата множественного коэффициента корреляции (коэффициента детерминации, «R-квадрат»);

- числа наблюдений n (число факторов обозначается k, см. ниже);

- нормированного коэффициента детерминации, объективно определяющего достоверность связи, так как, в отличие от обычного коэффициента детерминации, он не зависит от числа опытов (n) и числа факторов (k):

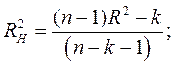(4.1)

- стандартной ошибки единичного наблюдения:

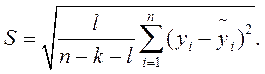(4.2)

2. Таблица «Дисперсионный анализ» включает в себя обусловленные регрессией («Регрессия»), необусловленные регрессией («Остаток») и суммарные:

- число степеней свободы df;

- сумму квадратов разностей (дисперсии SS);

- оценки дисперсий, приходящихся на одну степень свободы (MS).

Кроме того, выводятся расчётное значение F-критерия Фишера ( 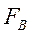) и «значимость F». Таким образом, в отличие от полного дисперсионного анализа (см. главу 4), табличное «критическое» значение F-критерия Фишера в данном случае не представлено. Поэтому вывод о существенности влияния рассматриваемых факторов в данном случае можно делать из сравнения величины «значимости F» с принятым уровнем доверительной вероятности α. При «значимость F» < α делается вывод о существенности влияния рассматриваемых факторов и правомерности проводимого регрессионного анализа.

3. Таблица результатов собственно регрессионного анализа(информация об уравнении регрессии) включает в себя:

- значение свободного члена уравнения 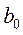(Y-пересечение);

- коэффициенты регрессии 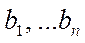для каждого фактора;

- «Стандартную ошибку» коэффициентов регрессии ;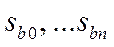

-«t-статистику» - расчётные значения коэффициентов Стьюдента для соответствующих коэффициентов регрессии ;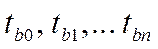

- «P-Значение» - вероятность значимости для соответствующих коэффициентов регрессии;

- нижние и верхние интервальные оценки (отклонения) для коэффициентов регрессии с 95-процентной и любой другой (заданной) доверительной вероятностью.

Поскольку «критические» (табличные) значения коэффициентов Стьюдента в этой таблице не приводятся, о достоверности рассчитанных коэффициентов регрессии можно судить по величине «P-Значения» в сравнении с принятым уровнем доверительной вероятности α. При «P-Значение» < α делается вывод о достоверности коэффициентов регрессии. В противном случае делается вывод, что регрессионная модель нуждается в коррекции (см. § 4.2).

Кроме того, при включённых дополнительных опциях выводятся следующие добавочные таблицы:

1.«Вывод остатка», где представлены:

– «Наблюдение» - порядковый номер значения отклика (у) в таблице исходных данных;

– «Предсказанное » - значение отклика ( ), рассчитанное по уравнению регрессии;

– «Остатки» - 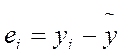(см. выше);

– «Стандартные остатки» (см. выше).

2. «Вывод вероятности», где представлены:

– Персентиль - рассчитывается для каждого значения у;

– у - значения отклика, расположенные в порядке возрастания.

3.4.3.2 Функции EXCEL, связанные с инструментом «Регрессия»

Во многих случаях нет необходимости в полном регрессионном анализе. Тогда возможно использование некоторых функций программы MS EXCEL, в той или иной мере связанных с регрессионным анализом: НАКЛОН, ОТРЕЗОК, СТОШУХ, ЛИНЕЙН, ПРЕДСКАЗ, ТЕНДЕНЦИЯ, ЛГРФПРИБЛ, РОСТ. (Кроме того, в отличие от инструмента «Регрессия», функции ЛГРФПРИБЛ и РОСТ определяют нелинейную регрессию, см. ниже.)

Первые три из отмеченных выше функций имеют всего два аргумента: «известные значения y» и «известные значения x», т.е. все они имеют сходные окна (на рис. 4.4 представлено окно функции НАКЛОН).

Функция НАКЛОН устанавливает наклон линии линейной регрессии для точек данных, образованных известными значениями y_i и известными значениями x_i. Наклон определяется как частное от деления расстояния по вертикали на расстояние по горизонтали между двумя точками прямой, т.е. наклон - это скорость изменения значений вдоль прямой. Иначе говоря, результат вычисления функции НАКЛОН представляет собой коэффициент a₁ в уравнении регрессии 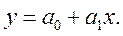(Результат расчёта этой и других функций, определяющих одно значение, появляется в окне аргументов сразу после внесения данных до нажатия «ОК».)

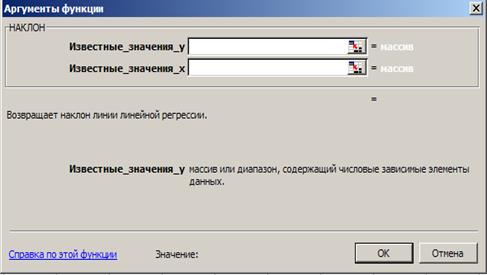
Рис. 4.4. Аргументы функции НАКЛОН

Функция ОТРЕЗОК, имеющая те же аргументы (известные значения x и известные значения y), что и функция НАКЛОН (рис. 4.4), вычисляет точку пересечения линии парной линейной регрессии с осью y, т.е. при x = 0. Иначе говоря, результат вычисления функции ОТРЕЗОК представляет собой коэффициент a₀ в уравнении регрессии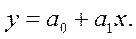

Функция СТОШУХ, имеющая те же аргументы, что и функции НАКЛОН, ОТРЕЗОК (рис. 4.4), принципиально отличается от них - она определяет не усреднённые результаты расчёта регрессионной модели, а стандартную ошибку предсказанных значений y в этой модели. Стандартная ошибка - это мера среднего рассеивания наблюдаемых значений (точек) вокруг подобранной линии регрессии, дающая некоторое представление о надежности уравнения регрессии для производства прогнозных расчетов. (Эта величина присутствует также в таблице «Регрессионная статистика» результатов регрессионного анализа.) Для парной регрессии стандартная ошибка оценки определяется следующим образом:

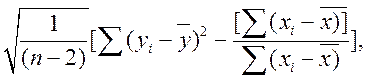(4.3)

где 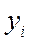- i-е фактическое значение результативного признака;

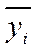- i-е теоретическое значение результативного признака, т.е. полученное по уравнению регрессии для .

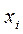Функция ЛИНЕЙН (рис. 4.5) рассчитывает статистику для ряда с применением метода наименьших квадратов путём вычисления линейной зависимости, которая наилучшим образом аппроксимирует имеющиеся данные.

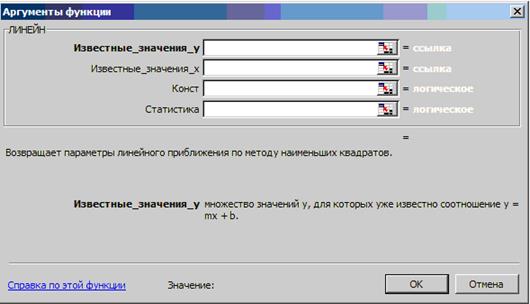
Рис. 4.5. Аргументы функции ЛИНЕЙН

Функция ЛИНЕЙН, в отличие от предыдущих функций, может использоваться для расчёта множественной регрессии (в случае задания нескольких диапазонов значений x), имеющей вид

y = m₁x₁ + m₂x₂ + ... + b. (4.4)

Если массив «известные значения y» в данном случае (рис. 4.5) и в других функциях задан столбцом, то каждый столбец массива «известные значения x» интерпретируется как отдельная переменная. Наоборот, если массив «известные значения y» задан строкой, то каждая строка массива «известные значения x» интерпретируется как отдельная переменная. При вводе «вручную» массива констант в качестве, например аргумента «известные значения x», следует использовать точку с запятой для разделения значений в одной строке и двоеточие для разделения строк. (Знаки-разделители могут быть различными в зависимости от настроек, заданных в окне «Язык и стандарты», открываемом с панели управления.)

Аргумент «Конст» (рис. 4.5) в данном случае и в других функциях - логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0. Если «Конст» имеет значение ИСТИНА или отсутствует, то b вычисляется обычным образом. Если «Конст» имеет значение ЛОЖЬ (ставится значение 0), то b в уравнении (4.4) полагается равным 0 и значения m подбираются так, чтобы выполнялось соотношение

y = m₁x₁+ ... + m_nx_n.

Статистика - логическое значение, которое указывает, требуются ли дополнительные статистические данные по регрессии. Если аргумент «Статистика» имеет значение 0 («ЛОЖЬ») или отсутствует, то функция ЛИНЕЙН подсчитает только коэффициенты регрессии. Если в качестве аргумента «Статистика» представлено любое другое число («ИСТИНА»), то производится расчёт дополнительной статистики.

Если для вывода результатов расчёта в MS EXCEL требуется не одна ячейка, необходимо предварительно выделить массив ячеек. Для функции ЛИНЕЙН необходимый массив состоит из пяти строк и числа столбцов, равного n +1. После введения всех аргументов необходимо набрать комбинацию клавиш CTRL+SHIFT+ENTER.(При нажатии «ОК» будет подсчитан только коэффициент при x.)

В дополнительную регрессионную статистику входят:

- стандартные значения ошибок коэффициентов m₁, m₂,... и постоянной b;

- коэффициент детерминации;

- стандартная ошибка для оценки y;

- F-статистика (F-наблюдаемое значение);

- степени свободы для нахождения F-критических значений;

- регрессионная сумма квадратов (sstotal);

- сумма квадратов остатков (ssresid).

Тогда сумма квадратов, обусловленных регрессией, может быть получена следующим образом: ssreg = sstotal - ssresid. То есть в рамках функции ЛИНЕЙН могут быть решены и задачи дисперсионного анализа. Таким образом, возможности функции ЛИНЕЙН с дополнительной статистикой в значительной степени сравнимы с возможностями инструмента «Регрессия». К её недостаткам относится то, что выводимые в определённом порядке результаты никак не обозначены. Поэтому для получения полного регрессионного анализа рекомендуется пользоваться инструментом «Регрессия».

Функция ТЕНДЕНЦИЯ (рис. 4.6) определяет значения в соответствии с линейным трендом; аппроксимирует прямой линией (по методу наименьших квадратов) массивы известные значения y и известные значения x; рассчитывает значения y в соответствии с этой прямой для заданного массива новых значений x.

Рис. 4.6. Аргументы функции ТЕНДЕНЦИЯ

В аргументах функции ТЕНДЕНЦИЯ (рис. 4.6) массив «известные значения x» может содержать одно или несколько множеств переменных. Если используется только одна переменная, то известные значения y и известные значения x могут задаваться в любой форме при условии, что они имеют одинаковую размерность. Если в «известных значениях x» используется более одной переменной, то известные значения y должны быть вектором (т.е. интервалом высотой в одну строку или шириной в один столбец).

Аргумент «Новые значения x» - новые значения x, для которых ТЕНДЕНЦИЯ рассчитывает соответствующие значения y. «Новые значения x» должны содержать такое же количество (и так же расположенных) столбцов или строк, как и «известные значения x».

Можно использовать функцию ТЕНДЕНЦИЯ (для одного фактора x) для аппроксимации полиномиальной кривой, проводя регрессионный анализ для той же переменной, предварительно возведённой в различные степени. (Эффективнее использовать для этой цели графические опции, описанные в главе 5.)

Функция ПРЕДСКАЗ рассчитывает для парной регрессии прогнозируемое значение результативного признака в соответствии с линейным трендом (рис. 4.7).

Рис. 4.7. Аргументы функции ПРЕДСКАЗ

Функция ПРЕДСКАЗ является частным случаем функции ТЕНДЕНЦИЯ, когда последняя применяется к парной регрессии и её аргумент «новые значения х» имеет размерность в одну ячейку. Аргумент «х»: точка данных, для которой предсказывается значение у (рис. 4.7).

Функция ЛГРФПРИБЛ (рис. 4.8) сходна с функцией ЛИНЕЙН, но в отличие от последней аппроксимирует связь исследуемых параметров не прямой линией, а экспоненциальной кривой.

Уравнение кривой в случае нескольких массивов x имеет вид

y = b×(m₁^x1) ×…×(m_n^xn), (4.5)

где значения m являются основанием, возводимым в степень x, а значения b постоянны.

Рис. 4.8. Аргументы функции ЛГРФПРИБЛ

«Конст» (рис. 4.8) - логическое значение, как и в функциях, описывающих линейную регрессию. Но в данном случае оно указывает, требуется ли, чтобы константа b была равна 1 (единице). Если «Конст» имеет значение ИСТИНА или отсутствует, то b вычисляется обычным образом. Если «Конст» имеет значение ЛОЖЬ, то значения m подбираются так, чтобы выполнялось b = 1.

При выведении полной статистики (опция «Статистика») её структура полностью соответствует структуре, выводимой в этом случае функцией ЛИНЕЙН, и включает коэффициенты регрессии, их стандартные отклонения, число степеней свободы, коэффициент детерминации и суммы квадратов остатков.

Функция РОСТ (рис. 4.9) также применяется для аппроксимации связи x- и y-значений экспоненциальной кривой, но по сравнению с функцией ЛГРФПРИБЛ решает более скромные задачи - рассчитывает значения y для новых значений x, не касаясь рассеяния и статистики.

Рис. 4.9. Аргументы функции РОСТ