Дробный факторный эксперимент
При большом числе учитываемых в эксперименте факторов ПФЭ становится громоздким, затратным и требует большое время для своего проведения, так как число опытов с ростом k увеличивается по экспоненте, см. выше. Число опытов можно сократить, если априори известно, что на процесс не оказывают влияния те или иные взаимодействия; действительно, в реальной ситуации некоторые взаимодействия факторов особенно высокого порядка (т. е. включающих большое число символов) не влияют на выходной параметр. В этом случае можно использовать так называемые дробные реплики от ПФЭ или дробный факторный эксперимент (ДФЭ).
Предположим, что необходимо получить математическое описание процесса при трех учитываемых факторах Х1, Х2 и Х3 оказывающих влияние на функцию отклика У.
При использовании ПФЭ для определения коэффициентов полинома 1-го порядка необходимо провести восемь опытов (23) в соответствии с матрицей планирования, приведенной в табл. 4.2. Число номеров опытов должно быть не менее числа коэффициентов полинома, в соответствии с которым планируется эксперимент. В данном случае предполагаемая математическая модель, описывающая исследуемый процесс, имеет вид полинома (4.4), содержащего восемь коэффициентов. Однако, если взаимодействие между факторами Х1, Х2 и Х3 отсутствует, можно ограничиться четырьмя опытами. В этом случае можно воспользоваться матрицей планирования ПФЭ для двух факторов Х1 и Х2 приведенной в табл. 4.1, заменив в ней обозначение х1бх2б на х3б, соответствующее безразмерному значению фактора Хъ на верхнем и нижнем его уровнях. Чередование знаков в этом столбце соответствует результату перемножения безразмерных значений двух других факторов (Х1 и Х2), т. е. остается неизменным после замены символов в матрице планирования, которая после введения в нее третьего фактора остается ортогональной. Эксперимент в этом случае будет ставиться уже с включением третьего фактора, изменяющегося согласно столбцу х1бх2б ПФЭ (табл. 4.1), а предполагаемая математическая модель будет иметь вид полинома 1-го порядка, не учитывающего взаимодействия факторов, т. е.
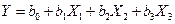 , (4.9)
, (4.9)
Такой сокращенный план содержит половину опытов от требуемого их числа 2k согласно плану ПФЭ (в нашем случае четыре опыта вместо восьми) и называется полурепликой от ПФЭ типа 2k. Условное обозначение такого плана: ДФЭ типа 2k-1, где k - число учитываемых в эксперименте факторов; 1 число взаимодействий, замененных факторами, учитываемых в эксперименте. Для рассматриваемого случая трех факторов Х1 Х2 Х3 матрица планирования ДФЭ типа 23-1будет иметь вид, представленный в таблице….
Таблица … Матрица планирования ДФЭ типа 23-1
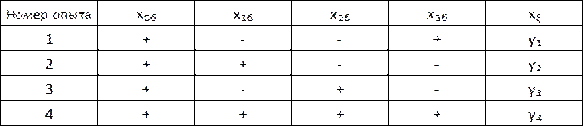
Приведенное планирование эксперимента дает возможность при обработке и анализе его результатов оценить в полиноме (4.9) свободный член Ьо и коэффициенты при линейных членах Ьь Ь2 и Ь3. Но при этом предполагается, что полностью отсутствует или пренебрежительно мало влияние на функцию отклика эффектов взаимодействия факторов исследуемого процесса. Только в этом случае математическая модель, представленная полиномом, в котором отсутствуют члены, учитывающие эти взаимодействия (так как соответствующие им коэффициенты равны нулю), может быть адекватна исследуемому процессу.
При использовании матрицы планирования ДФЭ нужно всегда помнить, что мы получаем совместную оценку нескольких эффектов: факторов и их взаимодействий. Действительно,
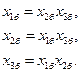 (4.10)
(4.10)
Поэтому подсчитываемые в дальнейшем (см. гл. 5) значения линейных коэффициентов Ь1, Ь2 и Ь3 полинома по экспериментальным значениям функции отклика будут всегда включать также значения коэффициентов, учитывающих эффект влияния взаимодействия факторов на функцию отклика. В результате этого подсчитанные значения коэффициентов полинома (4.9) фактически будут иметь следующий вид:
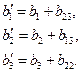 (4.11)
(4.11)
где b1 b2 и Ь3 - значения линейных коэффициентов полинома (4.9); а ь' - полученные их значения при наличии эффекта взаимодействия факторов на функцию отклика.
Часто имеет смысл начинать исследования с ДФЭ. Если у исследователя появились сомнения в том, что какие-то взаимодействия, ранее не включенные в план эксперимента, могут влиять на выходной параметр, он всегда имеет возможность расширить матрицу планирования до ДФЭ меньшей дробности или ПФЭ и найти раздельную оценку интересующих его эффектов.
Центральные композиционные планы
Описанный выше ДФЭ наиболее часто используется для сокращения числа опытов при двухуровневом планировании для получения линейной модели, то есть на первой стадии планирования эксперимента. При переходе исследователя от «грубой» модели к более точным моделям, например, при исследовании области экстремума, см. ниже § 4.3, осуществляется переход от полинома 1-го порядка вида (4.2) к полиному 2-го порядка (4.6).
Для вычисления полинома второго порядка число уровней должно быть, как минимум, три. В ПФЭ 3k при k = 2 потребуется проведение минимум девяти опытов, а для трех факторов (k = 3), их число резко возрастает до 27. Поэтому при увеличении числа учитываемых факторов применение ПФЭ 33 не рационально, так как это планирование характеризуется резким увеличением объема эксперимента. В этом случае (при многоуровневом планировании) используется другой способ сокращения число опытов - построение центральных композиционных планов (ЦКП).
Ядром ЦКП являются линейные ортогональные планы, что обеспечивает большое преимущество ЦКП. Действительно, если гипотеза о линейности математической модели, соответствующей исследуемому процессу, в результате анализа экспериментальных данных не подтвердилась, то нет необходимости ставить все эксперименты заново для получения модели более высокого порядка. Достаточно добавить несколько специально спланированных экспериментальных точек.
Поясним на примере с тремя независимыми факторами Х1 Х2 и Х3. Предположим, что для нахождения линейной модели применен ПФЭ 23, экспериментальные точки которого находятся в вершинах куба. В результате анализа экспериментальных данных установлено, что имитационная математическая модель в виде полинома 1-го порядка не адекватна исследуемому процессу. Тогда проводится опыт в центре плана, в точке (0; 0; 0),. Для повышения достоверности полученного экспериментального значения функции отклика у0в центре плана и её дисперсии, эти опыты повторяют. Подсчитанное среднее значение функции отклика уосравнивают с теоретическим значением b0, которое несложно получить из разработанной линейной модели процесса в результате ранее проведенного ПФЭ 23.
По разности b0- Уооценивают кривизну поверхности отклика. При подтверждении неадекватности линейной модели ставятся дополнительные опыты для значений факторов, превышающих их абсолютные значения по верхнему и нижнему уровням (в безразмерных величинах). Эти значения должны быть больше единицы по абсолютным значениям, установленным в предшествующем плане ПФЭ. Таким образом, в ПФЭ 23, к ранее проведенным восьми опытам добавляются еще семь опытов (включая опыт в центре плана), шесть из которых соответствуют «звездным точкам». «Звездные точки» (рис. 4.6) представляют собой два уровня варьирования каждого из трех факторов, значения которых лежат за пределами граней куба. Все «звездные точки» расположены на расстоянии большем, чем ± 1 от центра плана и лежат на поверхности сферы диаметром 2а. Общее число опытов центрального композиционного плана при k факторах составит
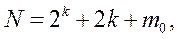 (4.18),
(4.18),
где 2k - число «звездных точек»; т0 - число опытов в центре плана, а общее число уровней варьирования ЦКП равно пяти.
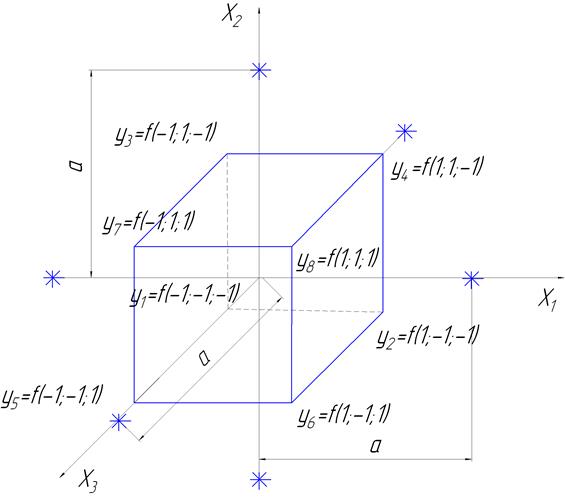
Рис. 4.6. Расположение экспериментальных точек в ЦКП, соответствующем полиному 2-го порядка для трех независимых переменных
В теории планирования экспериментов для получения моделей 2-го порядка различают несколько типов ЦКП. Наибольшее распространение получили ортогональный и рототабельныйЦКП.
Центральный композиционный ортогональный план (ЦКОП).При составлении матрицы планирования эксперимента этот план предусматривает проведение только одного опыта, условия которого соответствуют начальным значениям всех учитываемых факторов (в центре плана), т. е. mо=1. Поэтому для ЦКОП выражение (4.18) примет вид
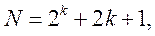 (4.19)
(4.19)
Соответствующая матрица ЦКОП для имитационной модели исследуемого процесса, соответствующая полиному 2-го порядка. представлена таблицей 4.4.
Таблица 4.4 Матрица центрального композиционного ортогонального плана
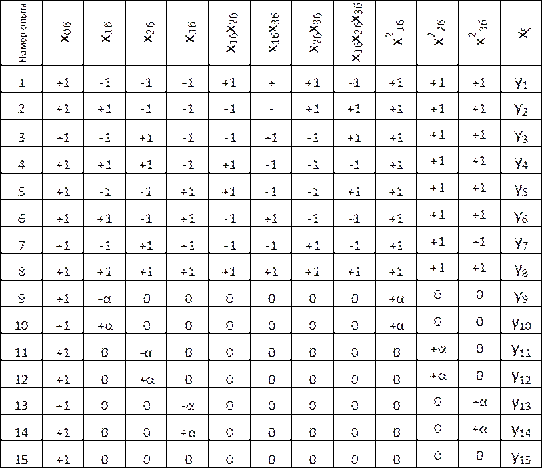
Как видно из таблицы, ЦКОП при k = 3 содержит всего 15 опытов, в то время как ПФЭ 33 потребовал бы проведения 27 опытов. Следует также обратить внимание на то, что условие ортогональности матрицы выполняется только для линейных членов соответствующего полинома 2-го порядка, представляющего собой имитационную модель вида
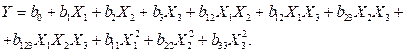 (4.20),
(4.20),
Из анализа табл. 4.4 нетрудно убедиться, что для матрицы ЦКОП условие ортогональности не выполняется для столбцов, соответствующих квадратичным членам полинома (4.20), так как
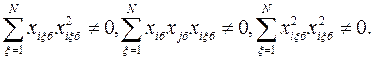
где i=l, k; х2iξб - безразмерное квадратичное значение i-то фактора, соответствующее ξ -му опыту.
Для приведения матрицы (табл. 4.4) к ортогональному виду необходимо провести преобразование квадратичных переменных x2
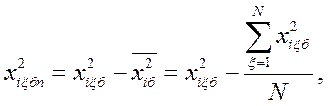 (4.21),
(4.21),
где 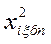 - преобразованное (п), безразмерное (б) квадратичное значение i-го фактора, соответствующее ξ -му опыту.
- преобразованное (п), безразмерное (б) квадратичное значение i-го фактора, соответствующее ξ -му опыту.
Для выполнения условия ортогональности матрицы ЦКОП, помимо преобразования столбцов, соответствующих квадратичным членам полинома (4.20), и приведения значений, стоящих в них, к виду (4.21), необходимо величину звездного плеча а выбирать из уравнений (подсчитанные значения приведены в табл. …) соответственно:
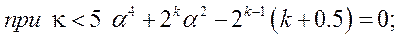 (4.22)
(4.22)
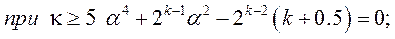 (4.23)
(4.23)
Ядро ЦКОП при k<5 составляет, как правило, ПФЭ типа 2k, а приk>5 - ДФЭ типа 2к-1,так как во втором случае полуреплика от ПФЭ вполне обеспечивает возможность независимой оценки линейных членов полинома (4.20) и членов, учитывающих эффект взаимодействия факторов.
Таблица …. Значения звездного плеча, подсчитанные на основании условий (4.22) и (4.23) для ЦКОП.
| k | ||||||
| α | 1,00 | 1,215 | 1,414 | 1,547 | 1,724 | 1,885 |
Преобразовав соответствующим образом матрицу ЦКОП,приведенную в табл. 4.4, получим матрицу ЦКОП,которая полностью соответствует условию ортогональности (табл. 4.5).
Для приведенной в табл. 4.5 матрицы ЦКОП будет соответствовать имитационная модель
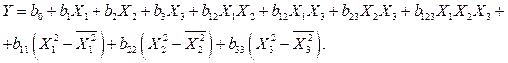 (4.24),
(4.24),
Для перехода от модели (4.24) к модели (4.20), необходимо пересчитать коэффициент b0, который будет в (4.20) определяться
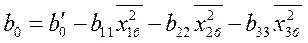
Таблица 4. Преобразованная матрица ЦКОП, отвечающая требованиям ортогональности
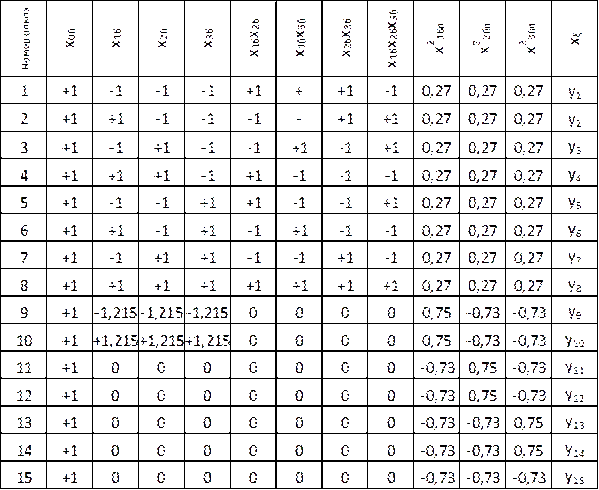
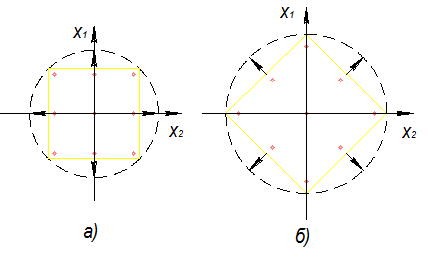
Рис. 4.7. Влияние расположения экспериментальных точек на вид информационных поверхностей до (а) и после (б) поворота осей координат [20].
Если выполняется условие (4.25), можно пользоваться полиномом 2-го порядка в общем виде (4.6) для проведения эксперимента в соответствии с преобразованной матрицей ЦКОП.
При применении ЦКОП получение идентичной информации во всех направлениях исследуемого пространства невозможно, так как дисперсии ошибок определения коэффициентов полинома (3.20) различны, т. е. точность предсказания выходной величины (значения функции отклика У) в различных направлениях факторного пространства неодинакова - информационные поверхности не являются сферами. Это можно пояснить с помощью рис. 4.7.
В § 4.2 было показано (см. рис. 4.4), что точность получаемого экспериментально представления об исследуемом объекте зависит от интервалов варьирования. При одинаковом взаимном расположении экспериментальных точек на рис. 4.7, а и б точность информации, получаемой с различных направлений меняется при повороте осей координат относительно экспериментальных точек. Так, на рис. 4.7,6 более точную информацию (экспериментальные точки расположены на большем расстоянии друг от друга) имеем по осям координат, а на рис. 4.7, а - с межосевых направлений, но в обоих случаях информационные поверхности далеки от сферических.
Центральный композиционный рототабельный план (ЦКРП)имеет то преимущество, чтоего информационная поверхность приближается к сферической т. е. точность У во всех направлениях на одинаковом расстоянии R от центра планирования становится практически одинаковой
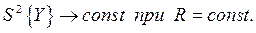
При этом, ЦКРП позволяет минимизировать ошибки в определении У, связанные с неадекватностью представления результатов исследования процесса имитационной моделью в виде полинома 2-го порядка. Это достигается тем, что, выбирая удаленные от центра плана «звездные точки» на осях координат для непрерывности информационной поверхности, они дополняются информацией из центра плана, представляющей собой сферу с нулевым радиусом, т. е. информацией равноточной во всех направлениях. Удельный вес этой информации в общем объеме информации увеличивается, что достигается увеличением числа опытов (m0) в центре плана. Ставя несколько экспериментов в центре плана, «накачиваем» информацию в центр плана (рис. 4.7), приближая информационные поверхности к сферам.
Таким образом, в ЦКРП, число опытов т0 в центре плана зависит от числа учитываемых в эксперименте факторов, т. е. mo=f(k). Так, для k = 3 mo = 6 (т. е. числу звездных точек). Это, безусловно, приводит к увеличению числа номеров опытов по сравнению с ЦКОП,но обеспечивает непрерывность информационной поверхности и ее идентичность независимо от поворота осей координат.
При реализации рототабельных планов можно отказаться от постановки параллельных опытов для оценки воспроизводимости экспериментов во всех точках плана, что уменьшит общее число опытов по сравнению с ЦКОП. В этом случае дисперсия воспроизводимости (дисперсия экспериментальных значений функции отклика в параллельных опытах) может быть оценена по параллельным экспериментам в центре плана.
Чтобы композиционный план был рототабельным, величина звездного плеча α выбирается из условий:
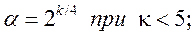 (4.26),
(4.26),
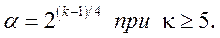 (4.27),
(4.27),
Подсчитанные значения звездного плеча α и число центральных точек m0, в зависимости от числа учитываемых в эксперименте факторов, приведены в табл. ….
Таблица … Размер «звёздного плеча» a и числа экспериментов в центре плана m0 в зависимости от числа рассматриваемых факторов k ЦКРП
| k | ||||||
| a | 1,414 | 1,682 | 2,00 | 2,00 | 2.38 | 2,83 |
| m0 |
Для k = 3 и соответственно m0 = 6 выражение (4.18) примет вид
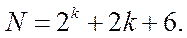 (4.28),
(4.28),
Таблица 4.6 Матрица центрального композиционного рототабельного плана
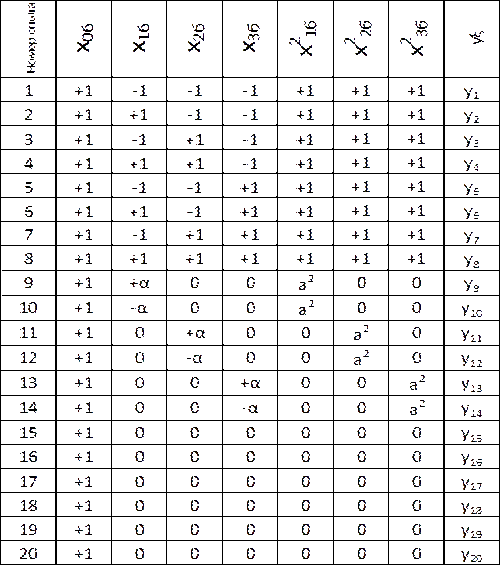
Из выражения (4.27) следует, что длятрех учитываемых в эксперименте факторов Х\, Х2 и Х3 в ЦКРП потребуется проведение не менее 20 опытов (табл. 4.6) по сравнению с 15-ю опытами в случае применения ЦКОП (табл. 4.4). Причем, все эти дополнительные пять опытов проводятся в центре плана.
Столбцы, соответствующие взаимодействию линейных факторов в матрице ЦКРП, приведенной в табл. 4.6, отсутствуют. Из сравнения табл. 4.6 с табл. 4.2 и табл. 4.4 (матрица для ПФЭ типа 23) нетрудно убедиться в том, что значения, приведенные в этих столбцах включительно до опыта № 8, были бы идентичны. Начиная с опыта № 9, значения, соответствующие взаимодействию линейных факторов, будут равны нулю, т. е. не влияют на оценку значимости соответствующего взаимодействию коэффициента в полиноме (4.20) при последующем анализе экспериментальных данных. Учитывая также тот факт, что оценка значимости этих коэффициентов, сделанная при обработке и анализе результатов эксперимента в процессе ранее проводимого ПФЭ, останется неизменной и в ЦКРП, приводить эти столбцы в матрице планирования ЦКРП не обязательно.
Из анализа табл. 4.6 видно, что матрица ЦКРП не соответствует условиям ортогональности для столбцов с квадратичными членами полинома (4.20). Поэтому оценка коэффициентов полинома 2-го порядка, проводимая но результатам эксперимента в соответствии с матрицей ЦКРП, не будет являться независимой. Но этот недостаток ЦКРП компенсируется более высокой точностью определения У во всех направлениях на одинаковом расстоянии R от центра плана. При этом следует учитывать тот факт, что ЦКРП использует независимую оценку коэффициентов полинома при линейных его членах, проведенную по результатам предыдущего полного или дробного факторного эксперимента.
Дата добавления: 2016-01-26; просмотров: 4568;
