Графический анализ остатков

Использование графического представления отклонений позво­ляет определиться с наличием гетероскедастичности. В этом случае по оси абсцисс откладывается объясняющая переменная X (либо ли­нейная комбинация объясняющих переменных 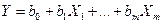), а по оси ординат либо отклонения 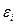, либо их квадраты 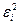. Примеры таких графиков приведены на рис. 4.

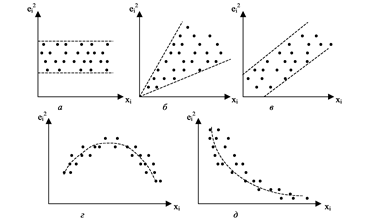
Рис. 4. Графический анализ остатков

На рис. 4. видно что, если все остатки находятся внутри полосы постоянной ширины, параллельной оси абсцисс, то предполагают постоянство дисперсии отклонений, т.е. выполнимость условия гомоскедастичности.

Если же наблюдаются систематические изменения в соотношениях между значениями переменной и квадратами остатков, то делают вывод о непостоянстве дисперсии, т.е. наличии гетероскедастичности.

Графический анализ отклонений является удобным и достаточно надежным в случае парной регрессии. При множественной регрессии этот анализ возможен для каждой из объясняющих переменных отдельно. Такой анализ наиболее целесообразен при большом количестве объясняющих переменных.

Тест Парка

Предполагается, что дисперсия 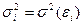является функцией i-го значения 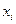объясняющей переменной.

Парк предложил следующую функциональную зависимость: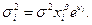

Прологарифмировав, получим: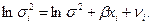

Т.к. дисперсии 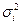неизвестны, то их заменяют

оценками квадратов отклонений .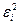

Алгоритм применения данного теста состоит в следующем.

1. Строится уравнение регрессии
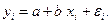
2. Для каждого наблюдения определяются
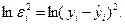
3. Строится регрессия

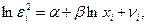
где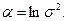

В случае множественной регрессии эта зависимость строится для каждой объясняющей переменной.

1. Проверяется статистическая значимость коэффициента 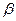на основе t-статистики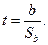

Если коэффициент статистически значим, то это означает наличие связи между 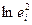и 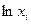, т.е. гетероскедастичности в данных.

Тест Глейзера

Тест Глейзера по своей сути аналогичен тесту Парка и дополняет его анализом других (возможно, более подходящих) зависимостей между дисперсиями отклонений и значениями объясняющей переменной .

Рассматривается зависимость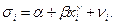

Оценивается регрессионная зависимость модулей отклонений (тесно связанных с 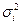) от .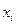

Поэтому рассматриваемая зависимость моделируется уравнением регрессии: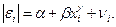

Регрессия осуществляется при различных значениях 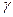. Обычно 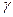= …, -1, -0.5, 0.5, 1,…, затем выбирается то значение, при котором коэффициент 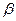оказывается наиболее значимым, т.е. имеет наибольшее значение t-статистики.

Статистическая значимость коэффициента в каждом конкретном случае фактически означает наличие гетероскедастичности.

Отметим, что как в тесте Парка, так и в тесте Глейзера для отклонений 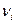может нарушаться условие гомоскедастичности. Поэтому данные критерии дополняются другими тестами.

Однако, во многих случаях используемые в тестах модели являются достаточно хорошими для определения гетероскедастичности.