Соотношение риска и доходности активов
Риск определяется как опасность, подверженность потере или ущербу. Он определяет вероятность того, что произойдет некое неблагоприятное событие. Но так как предполагается, что все активы должны порождать потоки денежных средств (cash flows), то неблагоприятным событием для инвестора является неполучение дохода от вложений в определенный актив. Соответственно вероятность неполучения дохода будет отражать степень рискованности данных инвестиций.
Выделяют автономный риск и риск актива в портфеле.
Автономный риск – это риск, с которым инвестор столкнется, если будет держать только этот актив.
Риск актива в портфеле формируется, когда потоки денежных средств, порождаемые рядом активов, хранимые инвестором одновременно, объединяются, а затем анализируются совместно. В результате, риск, который можно устранить включением актива в портфель вместе с другими и который отсутствует у диверсифицированных инвесторов называется диверсифицируемым риском. Релевантный риск отдельных акций – это их вклад в риск диверсифицированного портфеля ценных бумаг. Рыночный риск отражает риск падения рынка акций в целом и его невозможно устранить при помощи диверсификации. Поэтому от рыночного риска страдают все инвесторы, вложившие свои средства в акции.
Инвесторам нравится получать доход, но они не расположены принимать на себя риск. Следовательно, люди будут вкладывать деньги в рискованные активы, только если они предполагают получить с этого большие доходы. При прочих равных условиях, чем выше риск ценной бумаги, тем ниже оказывается ее цена, и тем выше средняя доходность, требуемая инвесторами.
Рассмотрим ряд формул, необходимых для оценки риска.
Ожидаемая средняя доходность актива : 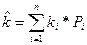 ;
;
где: ki – доходность акций в момент времени i;
Pi – вероятность получения доходности ki.
Чем более «сжатым» будет график распределения вероятности, тем ближе окажется фактическая доходность к ожидаемой. Следовательно, тем меньше вероятность, что действительная прибыль окажется значительно ниже предполагаемой. Чем более «сжато» распределение вероятности, тем ниже риск акции.
Мерой «сжатости» распределения вероятности является среднеквадратическое стандартное отклонение σ.
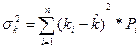
Чем меньше среднеквадратическое отклонение, тем более распределение вероятности «сжато» и, соответственно, тем ниже риск акций.
На практике исследователю чаще доступны только данные по доходности за несколько прошлых периодов времени. В этом случае среднеквадратическое отклонение оценивается следующим образом:
Эмпирическое 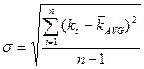 ;
;
где: kt – фактическая доходность;
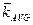 - среднегодовая доходность за n лет.
- среднегодовая доходность за n лет.
Для осуществления выбора между двумя вариантами вложения капитала, в которых один предполагает и большую доходность, и больший риск одновременно, следует использовать меру риска – коэффициент вариации, который вычисляется как среднеквадратическое отклонение, деленное на среднюю ожидаемую доходность.
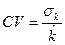 .
.
Коэффициент вариации отражает риск, который приходится на единицу доходности. Чем он выше, тем рискованнее будут вложения капитала.
Актив, хранимый в портфеле, обычно может считаться менее рискованным, чем актив, хранимый изолированно. И для портфельного инвестора или менеджера событие, связанное с тем, что отдельные акции падают или поднимаются в цене, не имеет принципиального значения – для него важны только доходность и риск его портфеля в целом.
Средняя (ожидаемая) доходность портфеля ценных бумаг – это средневзвешенное значение ожидаемых доходностей отдельных активов, входящих в портфель:
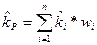 ;
;
Где:  – ожидаемая доходность отдельных активов;
– ожидаемая доходность отдельных активов;
wi – доля этих активов в портфеле из n акций.
Риск портфеля ценных бумаг будет ниже, чем средневзвешенное значение σi отдельных активов, и степень данного снижения будет зависеть от характера корреляции доходностей активов. В случае совершенной отрицательной корреляции риск портфеля равен 0. Но в действительности большинство акций положительно коррелированны, но не совершенно, поэтому, чем ниже коэффициент корреляции, тем ниже будет риск диверсифицированного портфеля. Хотя, некоторый риск всегда остается, и поэтому практически невозможно провести диверсификацию таким образом, чтобы полностью исключить влияние колебаний рынка акций в целом, влияющих на каждую из них.
Диверсифицированный риск вызывается такими непредвиденными событиями, как судебные иски к компаниям, забастовки, успешные и провальные маркетинговые программы, заключение или разрыв важных контрактов, а также другие события, которые индивидуальны для каждой отдельной фирмы. Поскольку эти события носят случайный характер, их влияние на портфель ценных бумаг может быть устранено с помощью диверсификации – негативные явления, имеющие место в одной фирме, могут быть компенсированы позитивными явлениями в другой.
Рыночный риск вызывается факторами, которые систематически влияют на большинство фирм: войны, инфляция, экономический спад и высокие процентные ставки. Поскольку на большинство акций все эти факторы влияют отрицательно, рыночный риск невозможно устранить с помощью диверсификации.
Доходность дифференцированного портфеля акций должна сравниваться с доходностью рыночного портфеля – портфеля, включающего все акции, присутствующие на рынке. Мера релевантного риска отдельных акций, которая называется бета - коэффициентом, определяется согласно модели САРМ (Capital Asset Prising Model), как количество риска, которое акции приносят в портфель, и рассчитывается следующим образом:
 ;
;
Где: σi – среднеквадратическое отклонение доходности акции;
σ M –среднеквадратическое отклонение доходности рынка;
riM - корреляция между доходностью i –й акции и доходностью рынка в целом.
Данное выражение показывает, что акции с высоким риском будут иметь и большой бета – коэффициент. Действительно, если все другие значения равны, акции с более высоким автономным риском должны вносить большую долю риска в портфель. Акции с высокой корреляцией с активами, присутствующими на рынке в целом, будут также иметь более высокий бета – коэффициент, а значит, и будут более рискованными. То есть значительная корреляция означает, что диверсификация не помогает, а значит, акции несут большую долю риска в составе портфеля.
Если b<1, то акции менее рискованны по сравнению с рынком в целом; если b=1, то акции имеют средний риск, равный рыночному риску; если b>1, то акции более рискованны, чем в среднем на рынке.
Портфель, состоящий из ценных бумаг с низким бета – коэффициентом, сам будет иметь низкий бета – коэффициент, поскольку бета – коэффициент портфеля является средневзвешенным значением бета – коэффициентов акций, входящих в его состав.
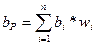 ;
;
где bP – это бета – коэффициент портфеля из n акций;
wi - доля стоимости портфеля, приходящегося на i – ю акцию;
bi – бета – коэффицент i – акции.
На практике бета – коэффициент рассчитывается с помощью модели парной регрессии, отражающей зависимость между доходностью акции и доходностью рыночного портфеля: ki=a+bi*kM+ε, которая и представляет собой модель САРМ.
Определим, какая рисковая премия будет достаточна инвесторам для принятого ими на себя риска, измеряемого с помощью бета – коэффициента.
 - премия за риск рыночного портфеля (премия за риск средней акции). Это дополнительная, сверх безрисковой, доходность, требуемая инвесторами для компенсации среднерыночного риска.
- премия за риск рыночного портфеля (премия за риск средней акции). Это дополнительная, сверх безрисковой, доходность, требуемая инвесторами для компенсации среднерыночного риска.
 - премия за риск i – й акции. Премия за риск акции будет меньше, равна или больше премии за риск рынка
- премия за риск i – й акции. Премия за риск акции будет меньше, равна или больше премии за риск рынка 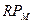 в зависимости от того, будет ли бета - коэффицент акции меньше, равен или больше 1.
в зависимости от того, будет ли бета - коэффицент акции меньше, равен или больше 1.
Соотношение между требуемой доходностью актива и риском можно графически представить линией рынка ценных бумаг (Security Market Line, SML), в соответствии с которой требуемую доходность акции i можно выразить следующим образом:
Требуемая доходность акции i = Безрисковая ставка +Премия за риск акции i = Безрисковая ставка + Рыночная премия за риск*Бета – коэффициент акции
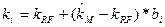 .
.
Дата добавления: 2016-01-26; просмотров: 2437;
