Ро-метод Полларда для дискретного логарифмирования.
Этот алгоритм осуществляет случайный поиск дискретных логарифмов, как и метод «шаг ребенка – шаг великана», но он требует меньшего объема памяти для хранения данных, поэтому предпочтительней для практических целей. В основе данного метода лежит та же идея, что и в основе ро-метода для факторизации – строится псевдослучайная последовательность, в которой находятся совпадающие элементы при помощи метода Флойда, а затем на основании полученной величины вычисляется искомый дискретный логарифм.
Пусть требуется вычислить logga в конечной группе G порядка n.
Группа G разбивается на три непересекающихся подмножества примерно равной мощности: G=S1US2US3, так чтобы 1  S2. Причем разбиение должно быть построено таким образом, чтобы проверка, к какому подмножеству принадлежит данный элемент x, была простой.
S2. Причем разбиение должно быть построено таким образом, чтобы проверка, к какому подмножеству принадлежит данный элемент x, была простой.
Например, если G=Zp, где p – простое число, то можно задать разбиение S1={1,…, 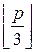 }, S2={
}, S2={ 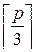 ,…,
,…, 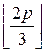 }, S3={
}, S3={  , … , p—1}, или разбиение может быть таким: если x mod 3=1, то x
, … , p—1}, или разбиение может быть таким: если x mod 3=1, то x 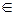 S1, если x mod 3=2, то x
S1, если x mod 3=2, то x 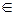 S2, если x mod 3=0, то x
S2, если x mod 3=0, то x 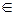 S3.
S3.
Далее на G задается последовательность x0, x1, x2, … , где x0=1, xi+1 вычисляется по xi посредством функции f для i≥0:
xi+1=f(xi)= 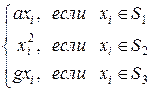
Вычисления проводятся в группе G, то есть если G=Zm, то вычисления следует производить по модулю m.
Такая последовательность групповых элементов может быть представлена двумя последовательностями u0, u1, u2,… и v0, v1, v2,… такими, что xi=  , u0=v0=0,
, u0=v0=0,
ui+1=  , vi+1=
, vi+1= 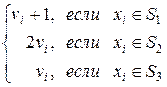
Вычисления в последовательностях u и v производятся по модулю n.
В силу того, что группа G – конечная, при помощи метода Флойда можно найти такие xi и x2i, что xi = x2i. Тогда  =
= 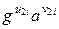
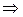
 . Логарифмируя по основанию g обе части данного уравнения, получим
. Логарифмируя по основанию g обе части данного уравнения, получим
(vi—v2i)logga≡(u2i—ui) (mod n)
Решая это сравнение, получим искомый логарифм. (Заметим, что если G=Z*m, то n=φ(m)).
Сложность данного метода составляет O( 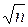 ) , где n – порядок группы G.
) , где n – порядок группы G.
Замечание. Метод может дать отказ в том случае, когда vi =v2i. Тогда следует назначить случайные значения от 0 до n—1 переменным u0, v0 , вычислить x0=  и повторить все шаги алгоритма.
и повторить все шаги алгоритма.
Замечание. В том случае, когда имеется достаточно места для хранения данных в процессе вычислений (например, когда G невелико или вычисления производятся вручную), можно обойтись без метода Флойда. Тогда следует хранить все члены последовательностей x, u и v до того, как xi = xj и дискретный логарифм находится из сравнения (vi—vj)logga≡(uj—ui) (mod n).
Пример.
G=Z*19, a=8, g=2.
Тогда n=φ(19)=18. Поскольку решение будем производить вручную, то не будем пользоваться методом Флойда.
Разбиение G на подмножества произведем следующим образом: если x mod 3=1, то x 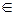 S1, если x mod 3=2, то x
S1, если x mod 3=2, то x 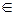 S2, если x mod 3=0, то x
S2, если x mod 3=0, то x 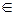 S3.
S3.
Вычисления будут производиться по формулам:
xi+1=f(xi)= 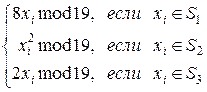
ui+1= 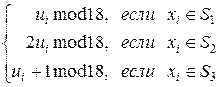 , vi+1=
, vi+1= 
| i | |||||||||
| xi | 18 | 18 | |||||||
| ui | |||||||||
| vi | |||||||||
| S | S1 | S2 | S1 | S3 | S2 | S1 | S1 | S3 | S3 |
x3=x8. Логарифм найдем из сравнения (v3—v8)log28≡(u8—u3) (mod 18)
-5 log28≡3(mod 18)
13 log28≡3(mod 18)
log28≡3·7(mod 18)
log28≡3(mod 18).
Действительно, 23≡8 (mod 19).
Ответ: log28≡3(mod 18).
Дата добавления: 2015-11-28; просмотров: 3589;
