Дифференциальное уравнение теплопроводности. Решение задач теплопроводности связано с определением поля температур и тепловых потоков

Решение задач теплопроводности связано с определением поля температур и тепловых потоков. Для установления зависимости между величинами, характеризующими явление теплопроводности, воспользуемся методом математической физики, который рассматривает протекание физических процессов в произвольно выделенном из всего рассматриваемого пространства элементарном объеме и в течение бесконечно малого промежутка времени. Это позволяет пренебречь изменением некоторых величин и существенно упростить выкладки.

При выводе дифференциального уравнения теплопроводности считаем, что тело однородно и изотропно (то есть физические свойства тела не зависят от выбранного в нём направления), физические параметры λ, с(теплоемкость), и ρ (плотность) постоянны, внутренние источники теплоты равномерно распределены в теле. Под внутренними источниками теплоты понимаются тепловыделения, например, в тепловыделяющих элементах атомных реакторов, или при прохождении тока в электрических проводниках. Внутренние источники теплоты характеризуются величиной q_v — количеством теплоты, которое выделяется в единице объема в единицу времени.

В основу вывода положен закон сохранения энергии, согласно которому вся теплота, выделенная внутренними источниками dQ_вн и внесенная извне в элементарный объем путем теплопроводности dQ_m за время dτ, идет на изменение внутренней энергии вещества, содержащегося в этом объеме:

.

(9.10)

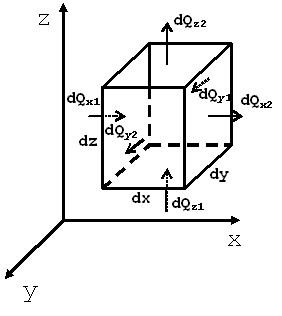
Выделим в теле элементарный параллелепипед с ребрами dx, dy, dz (рис. 9.1). Количество теплоты, которое проходит путем теплопроводности внутрь выделенного объема в направлении оси ОX через элементарную площадку dy·dz за время dτ:

.

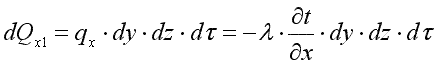На противоположной грани параллелепипеда температура получит приращение

и будет составлять .

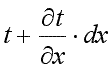
Количество тепла, отведенного через эту грань:

Разница количества теплоты, подведенного к элементарному параллелепипеду и отведенного от него, представляет собой теплоту, внесенную путем теплопроводности в направлении оси ОX:

.

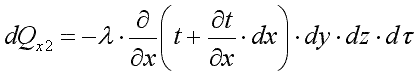
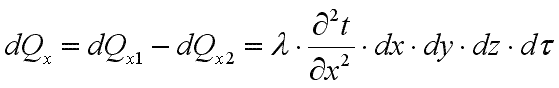Аналогично:

.

Полное количество теплоты внесено в элементарный параллелепипед путем теплопроводности

.

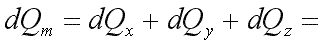
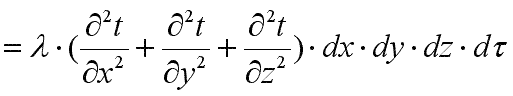Здесь произведение dx·dy·dz представляет собой объем элементарного параллелепипеда dv. Количество теплоты, которое выделилось в элементарном объеме за счет внутренних источников:

.

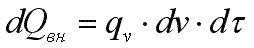Приращение внутренней энергии можно выразить через массу параллелепипеда ρ·dv, теплоемкость с и приращение температуры :

.

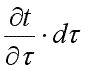
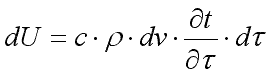Подставляя выражения для dQ_m, dQ_вн и dU в уравнение (9.10), после соответствующих сокращений получаем:

.

(9.11)

Сумма вторых частных производных любой функции в математическом анализе носит название оператора Лапласа и обозначается следующим образом:

.

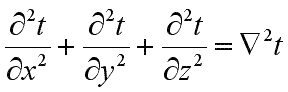Величину

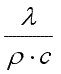
называют коэффициентом температуропроводности и обозначают буквой a.

В указанных обозначениях уравнение (9.11) примет вид:

.

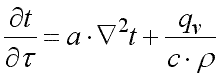(9.12)

Это уравнение называется дифференциальным уравнением теплопроводности или уравнением Фурье и лежит в основе математической теории теплопроводности.

Коэффициент температуропроводности a является физическим параметром вещества. Из уравнения (9.12) следует, что изменение температуры во времени для любой точки тела пропорционально величине a.

Краевые условия

Дифференциальное уравнение (9.12) описывает в самом общем виде все без исключения задачи теплопроводности. Для решения конкретной задачи необходимо к дифференциальному уравнению присоединить математическое описание частных ее особенностей. Эти дополнительные данные, которые характеризуют конкретное единичное явление, называются краевыми условиями, или условиями однозначности.

Существуют различные условия однозначности: геометрические — характеризующие форму и размеры тела, в котором протекает про­цесс теплопроводности; физические — характеризующие физические свойства тела; временные — характеризующие распределение температуры тела в начальный момент времени; граничные — характеризующие взаимодействие тела с окружающей средой. Граничные условия в свою очередь бывают трех родов:

1) первого рода, задается распределение температуры на поверхности тела в функции времени;

2) второго рода, задается плотность теплового потока для всей поверхности тела в функции времени;

3) третьего рода, задаются температура окружающей среды t_ж и закон теплоотдачи между поверхностью тела и окружающей средой — закон Ньютона—Рихмана:

,

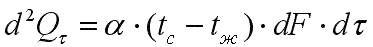(9.13)

где t_c — температура поверхности тела; α — коэффициент пропорциональности, называемый коэффициентом теплоотдачи, Вт/(м²·К). Коэффициент теплоотдачи численно равен количеству теплоты, отдаваемому или воспринимаемому единицей поверхности в единицу времени при разности температур между поверхностью тела и окружающей средой в один градус. Этот коэффициент учитывает все особенности явлении теплообмена, происходящие между поверхностью тела и окружающей средой. Плотность теплового потока, передаваемого от поверхности тела в окружающую среду,

.

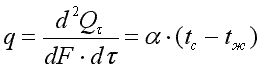(9.14)

Согласно закону сохранения энергии, эта теплота равна теплоте, подводимой к поверхности изнутри тела путем теплопроводности:

.

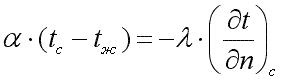Переписав последнее уравнение в виде:

,

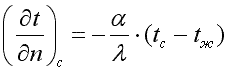(9.15)

получаем математическую формулировку граничных условий третьего рода. В результате решения дифференциального уравнения теплопроводности совместно с условиями однозначности можно найти температурное поле, а на основании закона Фурье — соответствующие тепловые потоки.