Теплопроводность через плоскую стенку при граничных условиях первого рода

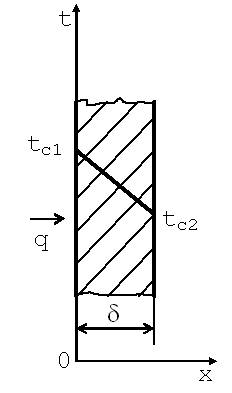
Рис. 9.2. Однородная плоская стенка

Рассмотрим однородную плоскую стенку толщиной δ (рис. 9.2). На наружных поверхностях стенки поддерживаются постоянные температуры t_с1 и t_с2. Коэффициент теплопроводности стенки постоянен и равен λ. При стационарном режиме

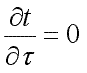
и отсутствии внутренних источников теплоты

q_v=0

дифференциальное уравнение теплопроводности примет вид:

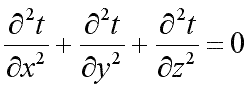
При заданных условиях температура будет изменяться только в направлении, перпендикулярном плоскости стенки (ось Оx). В этом случае

,

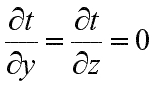и дифференциальное уравнение теплопроводности перепишется в виде:

.

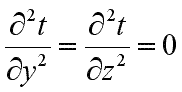
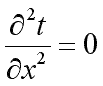(9.17)

Граничные условия первого рода запишутся следующим образом:

при x=0 t=t_c1; при x=δ t=t_c2.

Интегрируя уравнение (9.17), находим

.

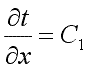После второго интегрирования получаем

.

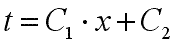(9.18)

Постоянные С₁ и С₂ определим из граничных условий:

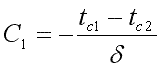
при x=0 t=t_c1, С₂=t_c1;

при x=δ t=t_c2=С₁·δ+t_c1,

Подставляя значения С₁ и С₂ в уравнение (9.18), получим уравнение распределения температуры по толщине стенки:

.

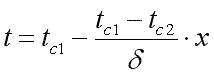(9.19)

Для определения плотности теплового потока, проходящего через стенку в направлении оси Оx, воспользуемся законом Фурье, согласно которому .

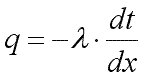
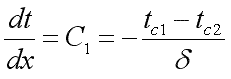
Учитывая, что , получим

.

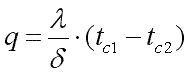(9.20)

Общее количество теплоты, которое передается через поверхность стенки F за время τ,

.

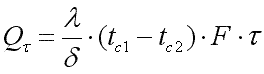(9.21)

Отношение

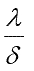
называют тепловой проводимостью стенки, обратную ей величину

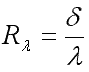
- термическим сопротивлением теплопроводности. Поскольку величина λ зависит от температуры, в уравнения (9.20), (9.21) необходимо подставить коэффициент теплопроводности λ_с, взятый при средней температуре стенки.