Выбор длины промежутков

Среднее время работы алгоритма зависит от длин промежутков (d), на которых будут находится сортируемые элементы исходного списка на каждом шаге алгоритма. Существует несколько подходов к выбору этих значений (N — длина сортируемого списка):

Ø при выборе последовательности значений 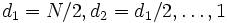в худшем случае алгоритм выполнит cN2 операций

Ø все значения (3j − 1) / 2 < N, 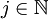; такая последовательность шагов приводит к алгоритму класса O(N3 / 2)

Ø все значения 2i3j < N, где 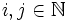, в порядке убывания; в таком случае количество операций понижается до O(N(logN)2)

Cортировка Шелла является довольно интересной модификацией алгоритма сортировки простыми вставками.

Рассмотрим следующий алгоритм сортировки массива a[0].. a[15].

1. Вначале сортируем простыми вставками каждые 8 групп из 2-х элементов (a[0], a[8[), (a[1], a[9]), ... , (a[7], a[15]).

2. Потом сортируем каждую из четырех групп по 4 элемента (a[0], a[4], a[8], a[12]), ..., (a[3], a[7], a[11], a[15]).

В нулевой группе будут элементы 4, 12, 13, 18, в первой - 3, 5, 8, 9 и т.п.

3. Далее сортируем 2 группы по 8 элементов, начиная с (a[0], a[2], a[4], a[6], a[8], a[10], a[12], a[14]).

4. В конце сортируем вставками все 16 элементов.

Очевидно, лишь последняя сортировка необходима, чтобы расположить все элементы по своим местам. Так зачем нужны остальные? На самом деле они продвигают элементы максимально близко к соответствующим позициям, так что в последней стадии число перемещений будет весьма невелико. Последовательность и так почти отсортирована. Ускорение подтверждено многочисленными исследованиями и на практике оказывается довольно существенным.

Единственной характеристикой сортировки Шелла является приращение - расстояние между сортируемыми элементами, в зависимости от прохода. В конце приращение всегда равно единице - метод завершается обычной сортировкой вставками, но именно последовательность приращений определяет рост эффективности. Использованный в примере набор ..., 8, 4, 2, 1 - неплохой выбор, особенно, когда количество элементов - степень двойки.

Однако гораздо лучший вариант предложил Р.Седжвик. Его последовательность имеет вид

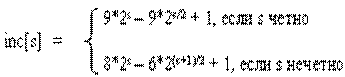
При использовании таких приращений среднее количество операций: O(n^7/6), в худшем случае - порядка O(n^4/3).

Сортировка Шелла

Сортировку Шелла придумал Дональд Л. Шелл. Ее необычность состоит в том, что она рассматривает весь список как совокупность перемешанных подсписков. На первом шаге эти подсписки представляют собой просто пары элементов. На втором шаге в каждой группе по четыре элемента. При повторении процесса число элементов в каждом подсписке увеличивается, а число подсписков, соответственно, падает. На рисунке ниже изображены подсписки, которыми можно воспользоваться при сортировке списка из 16 элементов.

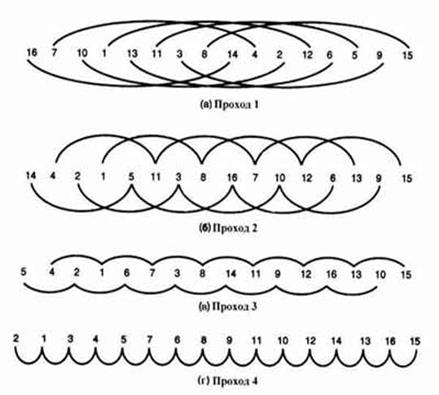
На рисунке (а) изображены восемь подсписков, по два элемента в каждом, в которых первый подсписок содержит первый и девятый элементы, второй подсписок - второй и десятый элементы, и так далее. На рисунке (б) мы видим уже четыре подсписка по четыре элемента в каждом. Первый подсписок на этот раз содержит первый, пятый, девятый и тринадцатый элементы. Второй подсписок состоит из второго, шестого, десятого и четырнадцатого элементов. На рисунке (в) показаны два подсписка, состоящие из элементов с нечетными и четными номерами соответственно. На рисунке (г) мы вновь возвращаемся к одному списку. Сортировка подсписков выполняется путем однократного применения сортировки вставками.