Сортировка слиянием
(См. стр. 430 Ф.М. Каррано и Дж.Дж.Причард)
Два важных алгоритма сортировки, основанных на принципе "разделяй и властвуй", сортировка слиянием и быстрая сортировка, имеют элегантное рекурсивное воплощение и чрезвычайно эффективны. В этом разделе мы рассмотрим сортировку массивов методом слияний, однако в главе 14 будет показано, что этот алгоритм можно обобщить на внешние файлы. Формулируя алгоритм, будем пользоваться обозначением отрезка массива theArray [first. . .last].
Алгоритм сортировки методом слияний является рекурсивным. Его эффективность не зависит от порядка следования элементов в исходном массиве. Допустим, что мы разделили массив пополам, рекурсивно упорядочили обе половины, а затем объединили их в одно целое, как показано на рис. 9.8. На рисунке показано, что части массива <1, 4, 8> и <2, 3> объединяются в массив <1, 2, 3, 4, 8>. В ходе слияния элементы, стоящие в разных частях массива, попарно сравниваются друг с другом, и меньший элемент отправляется во временный массив. Этот процесс продолжается до тех пор, пока не будет использована одна из двух частей массива. Теперь достаточно просто скопировать оставшиеся элементы во временный массив. В заключение содержимое временного массива копируется обратно в исходный массив.
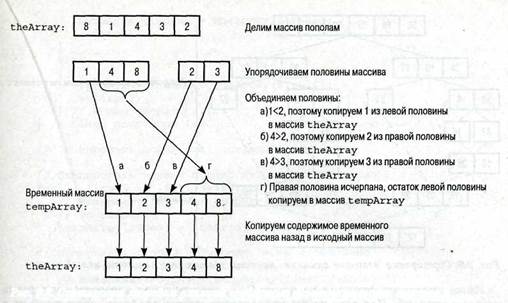
Рис. 9.8. Сортировка методом слияния с помощью вспомогательного массива
Хотя в результате слияния возникает упорядоченный массив, остается неясным, как выполняется сортировка на предыдущих этапах. Сортировка слиянием выполняется рекурсивно. Ее псевдокод имеет следующий вид.
mergesort(inout theArray:ItemArray,
in first:integer, in last: integer)
// Упорядочивает отрезок theArray[first..last],
// 1) сортируя первую половину массива;
// 2) сортируя вторую половину массива;
// 3) объединяя две упорядоченные половины массива.
If (first < last)
mid = (first + last)/2 // Определяем середину
// Сортируем отрезок theArray[first..mid] mergesort(theArray, first, mid)
// Сортируем отрезок theArray[mid+1..last] mergesort(theArray, mid + 1, last)
// Объединяем упорядоченные отрезки theArray[first..mid]
// и theArray[mid+1..last]
merge(theArray, first, mid, last)
} // Конец оператора if
// Если first >= last, операции завершены
Совершенно ясно, что основные операции этого алгоритма выполняются на этапе слияния, и все же, почему в результате возникает упорядоченный массив? Рекурсивные вызовы продолжают разделять части массива пополам, пока в них не останется только по одному элементу. Очевидно, что массив, состоящий из одного элемента, является упорядоченным. Затем алгоритм объединяет фрагменты массива, пока не образуется один упорядоченный массив. Рекурсивные вызовы функции mergesort и результаты слияний проиллюстрированы на рис. 9.9 на примере массива, состоящего из шести целых чисел.
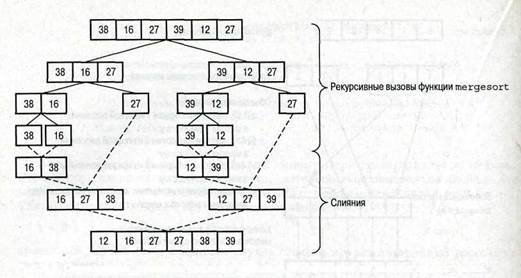
Рис. 9.9. Сортировка методом слияния массива, состоящего из шести целых чисел
Ниже приведена функция на языке C++, реализующая алгоритм сортировки методом слияний. Для того чтобы упорядочить массив theArray, состоящий из nэлементов, выполняется рекурсивный вызовmergesort (theArray, 0, n-1).
const intMAX_SIZE = максимальное-количество-элементов-массива,-
voidmerge(DataType theArray[], intfirst, intmid, intlast)
// _________________________________________________________
// Объединяет два упорядоченных отрезка theArray[first..mid] и
//theArray[mid+1..last] в один упорядоченный массив.
// Предусловие:first <= mid <= last. Оба подмассива
// theArray[first..mid] и theArray[mid+1..last] упорядочены
// по возрастанию.
// Постусловие:отрезок theArray[first..last] упорядочен.
// Замечание о реализации:функция выполняет слияние двух
// подмассивов во временный массив, а затем копирует его
// содержимое в исходный массив theArray.
// _________________________________________________________
Анализ.Поскольку основные операции в этом алгоритме выполняются на этапе слияния, начнем анализ с него. На каждом шаге происходит объединение подмассивов theArray [first. . .mid] и theArray [mid+1. . .last]. На рис. 9.10 показан пример, в котором требуется выполнить максимальное количество сравнений. Если общее количество элементов объединяемых отрезков массива равно п, то при их слиянии потребуется выполнить п-1 сравнений. (Например, на рис. 9.10показан массив, состоящий из шести элементов, следовательно, выполняется пять сравнений.) Кроме того, после сравнений осуществляется копировние п элементов временного массива в исходный. Таким образом, на каждом шаге слияния выполняется 3*п-1 основных операций.
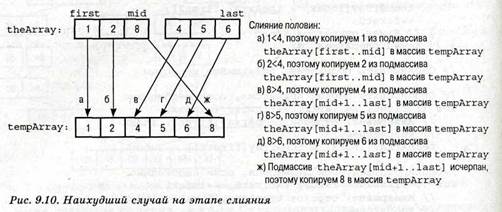
|
В функции mergesort выполняются два рекурсивных вызова. Как показано на рис. 9.11,если исходный вызов функции mergesort принадлежит нулевому уровню, то на первом уровне возникают два рекурсивных вызова. Затем каждый из этих вызовов порождает еще два рекурсивных вызова второго уровня и т.д. Сколько уровней рекурсии возникнет? Попробуем их подсчитать.
Каждый вызов функции mergesort делит массив пополам. На первом этапе исходный массив оказывается разделенным на две части. При следующем рекурсивном вызове функции mergesort каждая из этих частей снова делится пополам, образуя четыре части исходного массива. При следующем рекурсивном вызове каждая из этих четырех частей опять делится пополам, образуя восемь частей массива и т.д. Рекурсивные вызовы продолжаются до тех пор, пока части массива не станут содержать только по одному элементу, иными словами, пока исходный массив не будет разбит на п частей, что соответствует количеству его элементов, если число п является степенью двойки (n=2m), глубина рекурсии равна k=log2n Например, как показано на рис. 9.11, если исходный массив содержит восемь элементов (8=23), то глубина рекурсии равна 3. Если число п неявляется степенью двойки, глубина рекурсии равна 1+ log2n (округленное значение).
Исходный вызов функции mergesort (ypoвень 0) обращается к функции merge только один раз. Затем функция merge осуществляет слияние п элементов, выполняя 3*n-1 операций. На первом уровне рекурсии выполняются два вызова функции mergesort и, следовательно, функции merge. Каждый из этих двух вызовов приводит к слиянию n/2 элементов и требует выполнения 3*(n/2)-1 операций. Таким образом, на этом уровне выполняется 2*(3*(n/2)-1)=3*n-2 операций. На m-м уровне рекурсии выполняются 2т вызовов функции merge. Каждый из этих вызовов приводит к слиянию п/2т элементов, а общее количество операций равно 3*(n/2m)-2. В целом, 2m рекурсивных вызова функции merge порождает 3*n-2m операций. Таким образом, на каждом уровне рекурсии выполняется О(л) операций. Поскольку количество уровней рекурсии равно log2n или log2n+l, в наихудшем и среднем вариантах функция mergesort имеет сложность O(n*log2n). Посмотрите на рис. 9.3 и еще раз убедитесь, что величина O(n*log2n) растет намного медленнее, чем величина О(пг).
Хотя алгоритм сортировки слиянием имеет чрезвычайно высокое быстродействие, у него есть один недостаток. Для выполнения операции
Объединить упорядоченные подмассивы theArray[first...mid] и theArray[mid+1...last]
необходим вспомогательный массив, состоящий из п элементов. Если объем доступной памяти ограничен, это требование может оказаться неприемлемым.
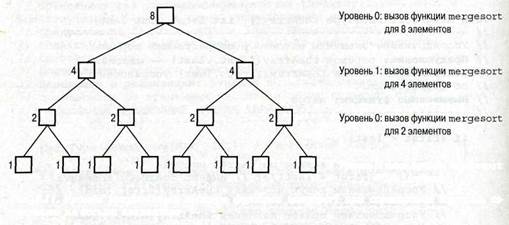
|
Уровень 0: вызов функции mergesort для 1 элемента
Рис. 9.11. Уровни рекурсивных вызовов функции mergesort при сортировке массива, состоящего из восьми элементов
Быстрая сортировка
Выберите в массиве theArray[first... last]опорный элемент р Поделите массив theArray[first... last] относительно элемента р
| Алгоритм быстрой сортировки разбивает массив на две части: в первую часть входят элементы меньше опорного, а во вторую — остальные |
Разбиение, показанное на рис. 9.12, характеризуется тем, что все элементы множества Si=theArray[first. . .pivotIndex-1] меньше опорного элемента р, а множество S2= theArray [pi votlndex+l. . .last] состоит из элементов, больших или равных опорному. Хотя из этого свойства не следует, что массив упорядочен, из него вытекает чрезвычайно полезный факт: если массив упорядочен, элементы, стоящие на позициях от first до pivotlndex-l, остаются на своих местах, хотя их позиции относительно друг друга могут измениться. Аналогичное утверждение выполняется и для элементов, стоящих на позициях от pivotlndex+l до last. Опорный элемент в полученном упорядоченном массиве останется на своем месте.
| В результате быстрой сортировки опорный элемент останется на |
| своем месте |
Такое разбиение массива определяет рекурсивный характер алгоритма. Разбиение массива относительно опорного элемента р порождает две задачи сортировки меньшего размера — сортировка левой (S1) и правой (S2) частей массива. Решив эти две задачи, мы получим решение исходной задачи. Иными словами, разбиение массива перед рекурсивными вызовами оставляет опорный элемент на своем месте и гарантирует, что левый и правый отрезки массива окажутся упорядоченными. Кроме того, алгоритм быстрой сортировки конечен: размеры левого и правого отрезка массива меньше размера исходного массива, причем каждый шаг рекурсии приближает нас к базису, когда массив состоит из одного элемента. Это следует из того факта, что опорный элемент р не принадлежит ни одному из массивов Sl и S2.
Псевдокод алгоритма быстрой сортировки выглядит следующим образом.
quicksort (inout theArray.- ItemArray,
in first:integer, in last:integer) // Упорядочивает массив theArray[first..last]
if (first < last)
Выбрать опорный элемент р из массива theArray[first..last] Разбить массив theArray[first..last] относительно
опорного элемента р // Разбиение имет вид theArray[first..pivotlndex..last]
// Упорядочиваем массив SI
quicksort(theArray, first, pivotlndex-l)
// Упорядочиваем массив S2
quicksort(theArray, pivotlndex+l, last) } // Конец оператора if // если first >= last, ничего не делаем
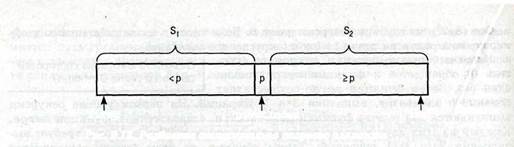
|
first pivotlndex last
Рис. 9.12. Разбиение относительно опорного элемента
| Перед разбиением поместите выбранный опорный элемент в ячейку theArray[first] |
Как выбрать опорный элемент? Если элементы массива записаны в произвольном порядке, в качестве опорного можно выбрать любой элемент, например theArray [first]. (Более детально процедура выбора опорного элемента будет рассмотрена позднее.) При разбиении массива опорный элемент удобно помещать в ячейку theArray [first], независимо от того, какой именно элемент выбран в качестве опорного.
Часть массива, в которой находятся элементы, еще не распределенные по отрезкам S1 и S2, называется неопределенной. Итак, рассмотрим массив, изображенный на рис. 9.14. Индексы first, lastS1, firstUnknown и last разделяют массив на три части. Отношения между опорным элементом и элементами неопределенной части theArray [firstUnknown. .last] неизвестны.
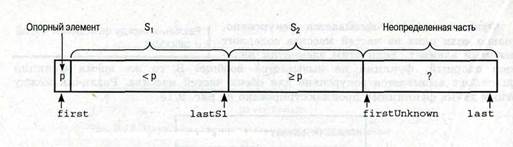
Puc. 9.14. Инвариант алгоритма разбиения
В процессе разбиения массива должно выполняться следующее условие.
Элементы множества S1 должны быть меньше опорного элемента, а элементы множества S2 — больше или равны ему.
Это утверждение является инвариантом алгоритма разбиения. Для того чтобы в начале алгоритма выполнялся его инвариант, необходимо проинициализировать индексы массива так, чтобы весь массив, кроме опорного элемента, считался неопределенным .
| lastSl = first firstUnknown = first + 1 |
В исходном положении все элементы, за исключением элемента theArray[first], относятся к неопре-
деленной части
Исходное состояние массива изображено на рис.15.
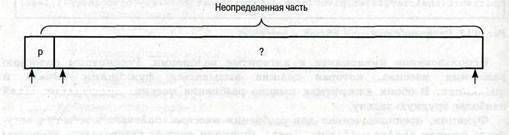
|
first firstUnknown last
lastSl
Puc. 9.15. Исходное состояние массива
На каждом шаге алгоритма разбиения проверяется один элемент из неопределенной части. В зависимости от его значения он помещается в множество S1 или S2. Таким образом, на каждом шаге размер неопределенной части уменьшается на единицу. Алгоритм останавливается, когда размер неопределенной части становится равным нулю, т.е. выполняется условие firstUnknown > last.
Рассмотрим псевдокод этого алгоритма.
partition (inout theArray:ItemArray,
in first:integer, in last:integer,
out pivotlndex:integer) // Разделяет массив theArray[first..last]
// Инициализация
Выбрать опорный элемент и поменять его местами
с элементом theArray[first]
р = theArray[first] // p — опорный элемент
// Задаем пустые множества S1 и S2, а неопределенную // часть массива инициализируем отрезком
// theArray[firat+l..last] lastSl = first firstUnknown = first + 1
// Определяем множества Sj и S2 while (firstUnknown <= last)
{
// Вычисляем индекс самого левого элемента // неопределенной части массива if (theArray[firstUnknown] < р)
Поместить элемент theArray[firstUnknown] в Si else
Поместить элемент theArray[firstUnknown] в S2 } // Конец оператора while
// Ставим опорный элемент между множествами S2 и S2 // и запоминаем его новый индекс
Поменять местами theArray[first] и theArray[lastSl] pivotlndex = lastSl
Алгоритм достаточно прост, но операция перемещения требует разъяснения. Рассмотрим два возможных действия, которые необходимо выполнить на каждой итерации цикла while.
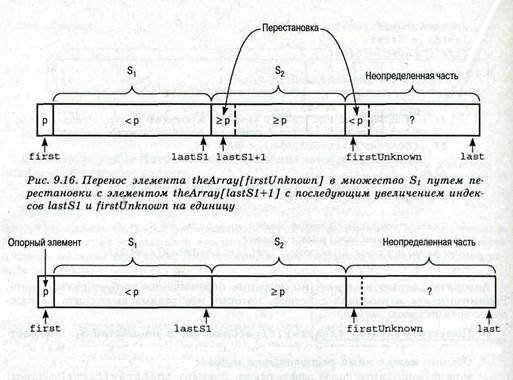
• Поместить элемент theArray [firstUnknown] в множество St. Множество S1 и неопределенная часть, как правило, не являются смежными. Обычно между ними располагается множество S2. Однако эту операциюможно выполнить более эффективно. Элемент theArray[firstUnknown] можно поменять местами с первым элементом множества S2, т.е. с элементом theArray[lastSl+l], как показано на рис. 9.16. Как быть сэлементом множества S2, который был помещен в ячейку theArray[firstUnknown]? Если увеличить индекс firstUnknown на единицу, этот элемент становится самым правым в множестве S2. Таким образом, для переноса элемента theArray [firstUnknown] в массив S1 необходимо выполнить следующие шаги.
Поменять местами элементы theArray[firstlnknown]
и theArray[lastSl+l] Увеличить индекс lastSl на единицу Увеличить индекс firstUnknown на единицу
• Эта стратегия остается верной, даже если множество S2 пусто. В этом случае величина lastSl+l равна индексу firstUnknown, и элемент просто остается на своем месте. Инвариант при этом не нарушается.
• Поместить элемент theArray [firstUnknown] в множество S2. Эту операцию легко выполнить. Напомним, что индекс крайнего правого элемента множества S2 равен firstUnknown-1, т.е. множество S2 и неизвестная часть являются смежными (рис. 9.17). Таким образом, чтобы переместить элемент theArray [firstUnknown] в множество S2, нужно просто увеличить индекс firstUnknown на единицу, расширяя множество S2 вправо.Инвариант при этом не нарушается.
После переноса всех элементов из неопределенной части в множества S1 и S2 остается решить последнюю задачу. Нужно поместить опорный элемент между множествами S1 и S2. Обратите внимание, что элемент theArray [lastSl] явля-
|
Рис. 9.17. Перенос элемента theArray[firstUnknown] в множество S2 после увеличения индекса firstUnknown на единицу
ется крайним правым элементом множества S1. Если поменять его местами с опорным элементом, тот станет на правильное место. Следовательно, оператор
pivotlndex = lastSl
позволяет определить индекс опорного элемента. Этот индекс можно использовать в качестве границы между множествами Sj и 5г. Результаты трассировки алгоритма разбиения массива, состоящего из шести целых чисел, когда опорным является первый элемент, показаны на рис. 9.18.
Прежде чем приступить к реализации алгоритма быстрой сортировки, проверим корректность алгоритма разбиения, используя его инварианты. Инвариант цикла, входящего в алгоритм, имеет следующий вид.
Все элементы множества S2 (theArray[first+1..lastSl] ) меньше опорного, а все элементы множества S2 (theArray[lastSl..firstUnknown-1]) больше или равны опорному
Напомним, что для определения правильности алгоритма с помощью его инвариантов, необходимо выполнить четыре шага.
1. Инвариант должен быть истинным с самого начала, до выполнения цикла. В алгоритме разбиения опорным элементом является theArray [first], неизвестной частью— отрезок массива theArray [first+1. .last], a множества S1 и S2 пусты. Очевидно, что при этих условиях инвариант является истинным.
2. Итерации цикла не должны нарушать инвариант. В алгоритме разбиения каждая итерация цикла переносит один элемент из неизвестной части в множество S1 или S2, в зависимости от его значения по сравнению с опорным. Итак, если до переноса инвариант был истинным, он должен сохраняться и после переноса.
3. Инвариант должен определять корректность алгоритма. Иными словами, из истинности инварианта должна следовать корректность алгоритма. Выполнение алгоритма разбиения прекращается, когда неопределенная область становится пустой. В этом случае каждый элемент отрезка theArray[first+1. .last] должен принадлежать либо множеству S1, либо множеству S2. В любом случае из корректности инварианта следует, что
алгоритм достиг своей цели.
4. Цикл должен быть конечным. Иными словами, нужно показать, что выполнение цикла завершится после конечного числа итераций. В алгоритме разбиения размер неопределенной части на каждой итерации уменьшается на единицу. Следовательно, после выполнения конечного количества итераций неопределенная часть становится пустой, и цикл завершается.

|
Рис. 9.18. Первое разбиение массива, когда опорным является первый элемент
Перед вызовом функции quicksort выполняется разбиение массива на части S1 и S2. Затем алгоритм упорядочивает отрезки S1 и S2 независимо друг от друга, поскольку любой элемент отрезка S1 находится левее любого элемента отрезка S2. В функции mergeSort, наоборот, перед рекурсивными вызовами никакая работа не выполняется. Алгоритм упорядочивает каждую из частей массива, постоянно учитывая отношения между элементами обеих частей. По этой причине алгоритм должен объединять две половины массива после выполнения рекурсивных вызовов.
Анализ. Основная работа в алгоритме quicksort выполняется на этапе разбиения массива. Анализируя каждый элемент, принадлежащий неопределенной части, необходимо сравнивать элемент theArray[firstunknown] с опорным и помещать его либо в отрезок S1, либо в отрезок S2. Один из отрезков S1 или S2 может быть пустым; например, если опорным элементом является наименьший элемент отрезка, множество S1 останется пустым. Это происходит в наихудшем случае, поскольку размер отрезка S2 при каждом вызове функции quicksort уменьшается только на единицу. Таким образом, в этой ситуации будет выполнено максимальное количество рекурсивных вызовов функции quicksort.
При следующем рекурсивном вызове функции quicksort функция partition просмотрит п-1 элемент. Чтобы распределить их по отрезкам, понадобится п-2 сравнений. Поскольку размер отрезка, рассматриваемого функцией quicksort, на каждом уровне рекурсии уменьшается только на единицу, возникнет п-1 уровней рекурсии. Следовательно, функция quicksort выполняет 1 + 2 + ...+ (n-1) = n * (n-1)/2 сравнений. Напомним, однако, что при переносе элемента в множество S2 выполнять перестановку элементов не обязательно. Для этого достаточно лишь изменить индекс firstUnknown.
Аналогично, если множество S2 при каждом рекурсивном вызове остается пустым, потребуется n * (n-1)/2 сравнений. Кроме того, в этом случае для переноса каждого элемента из неизвестной части в множество S1 придется выполнять перестановку элементов. Таким образом, понадобится * (n-1)/2 перестановок. (Напомним, что каждая перестановка выполняется с помощью трех операций присваивания.) Итак, в худшем случае сложность алгоритма quicksort равна О(n2).
Для контраста на рис. 9.20 продемонстрирован пример, когда множества S1 и S2 состоят из одинакового количества элементов. В среднем случае, когда множества S1 и S2 состоят из одинакового — или приблизительно одинакового — количества элементов, записанных в произвольном порядке, рекурсивных вызовов функции quicksort потребуется меньше. Как и при анализе алгоритма mergeSort, легко показать, что глубина рекурсии в алгоритме quicksort равна log2n или log2n+l. При каждом вызове функции quicksort выполняется m сравнений и не больше, чем m перестановок, где m — количество элементов в подмассиве, подлежащем сортировке.

|
Быстрая сортировка: наихудший вариант О(п2), средний вариант O(n*logn).
Таким образом, с большими массивами алгоритм
quicksort работает значительно быстрее, чем алгоритм insertionSort, хотя в наихудшем варианте они оба имеют приблизительно одинаковое быстродействие.
Алгоритм quicksort часто используется для сортировки больших массивов. Причина его популярности заключается в исключительном быстродействии, несмотря на обескураживающие оценки наихудшего варианта. Дело в том, что этот вариант встречается крайне редко, и на практике алгоритм quicksort отлично работает с относительно большими массивами.
Значительное различие между оценками сложности в среднем и наихудшем вариантах выделяет алгоритм быстрой сортировки среди остальных алгоритмов, рассмотренных в данной главе. Если порядок записи элементов в исходном массиве является "случайным", алгоритм quicksort работает по крайней мере не хуже любого другого алгоритма, использующего сравнения элементов. Если исходный массив совершенно не упорядочен, алгоритм quicksort работает лучше всех.
Алгоритм mergeSort имеет приблизительно такую же эффективность. В некоторых случаях быстрее работает алгоритм quicksort, в других — алгоритм mergeSort. Несмотря на то что оценка сложности алгоритма mergeSort в наихудшем варианте имеет тот же порядок, что и оценка сложности алгоритма quicksort в среднем варианте, в большинстве случаев алгоритм quicksort работает несколько быстрее. Однако в наихудшем варианте быстродействие алгоритма quicksort намного ниже.
| <== предыдущая лекция | | | следующая лекция ==> |
| ОТРИЦАТЕЛЬНЫЕ ПОСЛЕДСТВИЯ УСИЛЕНИЯ ПАРНИКОВОГО ЭФФЕКТА | | | Выбор длины промежутков |
Дата добавления: 2016-01-20; просмотров: 3426;
