Числа Ферма. Теорема Пепина.

Теорема.

Если число вида p=aⁿ+1 – простое, то 1) a – четное;

2) n=2^k для некоторого k.

Доказательство:

Четность a очевидна, так как иначе p было бы четным, а значит не простым.

Предположим теперь 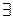m>2 - нечетное число : n= m·2^k. Тогда

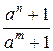=a^n—m—a^n—2m+…+a^3m—a^2m+a^m—a⁰ 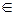Z.

Тогда (a^m+1)\(aⁿ+1), значит p – составное число. Предположение неверно, следовательно верно обратное.

□

Числа F_k= 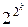+1 называются числами Ферма.

F₀=3, F₁=5, F₂=17, F₃=257, F₄=65739 – простые числа. Пьер Ферма выдвигал гипотезу о простоте всех чисел Ферма, но Леонардом Эйлером в 1732 г. была показана составность числа F₅.

В настоящее время существует следующий критерий проверки чисел Ферма на простоту:

Теорема Пепина

F_k – простое число .

Доказательство:

Пусть F_k – простое число. Тогда по критерию Эйлера для символа Лежандра,

.

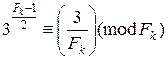В силу простоты, F_k не делится на 3.

Поэтому возможны два случая: F_kmod 3=1 или F_k mod 3=2.

Случай F_k mod 3=1 невозможен, так как это значило бы, что 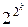mod 3 = 0, а это не так. Поэтому F_k mod 3=2, и тогда

□

На основании теоремы Пепина построен тест Пепина, проверяющий верность сравнения . Тест Пепина детерминированный, состоит из одной итерации и дает точный ответ о простоте или составности числа Ферма.

Числа Мерсенна.

Теорема 1

Если число вида p=aⁿ—1 – простое 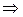1) a – четное;

2) n – простое.

Доказательство:

Четность а очевидна, так как иначе р было бы четным, а значит, составным.

Допустим, что n – не простое 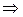n=mk. Тогда

=a^k(m—1)+a^k(m—2)+…+a^k+1 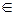Z.

Тогда (a^k—1)\(aⁿ—1), значит р – не простое число. Предположение неверно, значит верно обратное.

□

Простые числа вида M_p=2^p—1, где р – простое число, называются числами Мерсенна.

Теорема 2

Число вида M_p=2^p—1, где р>2 – простое число, является простым в последовательности, определенной равенствами u₀=4, u_i+1=(u_i²—2) mod M_p, выполняется u_p—2≡0(mod M_p).

■

Из Теорем 1 и 2 следует

Тест Лукаса-Лемера для чисел Мерсенна

Вход: Число Мерсенна M_n=2ⁿ—1.

Ш.1. Пробными делениями проверить, имеет ли n делители между «2» и 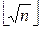. Если имеет, идти на Выход с сообщением «M_n – составное число».

Ш.2. Задать u=4.

Ш.3. n—2 раза вычислить u=(u²—2) mod M_n.

Ш.4. Если u=0, то «M_n – простое число», иначе «M_n – составное число».

Выход.

В настоящее время особое внимание уделяется двойным числам Мерсенна MM_p=2^Mp –1, например 7=M₃=MM₂. Алгоритм построения таких чисел следующий: сначала строится сравнительно небольшое простое число Мерсенна M_p, а затем по нему – двойное число Мерсенна MM_p, которое проверяется на простоту тестом Лукаса-Лемера минуя первый шаг.

Аналогично строятся тройные и т.д. числа Мерсенна. Например, тройным числом Мерсенна является 127=M₇=MMM₂.

Не для всех чисел Мерсенна существуют двойные и тройные числа. Например, MM₁₃ не является простым.

Первыми простыми числами Мерсенна являются M₂=3, M₃=7, M₅=31, M₇=127, M₁₃=8191, M₁₇, M₁₉, M₃₁.

На данный момент (2007 г.) не доказана конечность или бесконечность количества простых чисел Мерсенна.