Условная стойкость шифра Эль Гамаля.

Шифр ElGamal – симметричный шифр, основанный на теоретико-числовой проблематике. Напомним его конструкцию.

Параметры системы: p – простое число, α– порождающий элемент группы U_p;

Закрытый ключ для расшифрования: a – целое число, 1 ≤ a < p—1;

Открытый ключ для шифрования: β = α^a mod p.

Пусть имеется открытый тест x 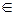U_p. Для шифрования берут случайное число k 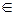Z_p—1 и вычисляются y₁=α^k mod p, y₂=xβ^k mod p. Затем пара (y₁,y₂) пересылается обладателю секретного ключа, а k уничтожается.

Для расшифрования необходимо вычислить x=y₂(y₁^a)^-1mod p.

Действительно, в результате расшифрования получим открытый текст:

y₂(y₁^a)^-1mod p=xβ^k(α^ka) ^-1 mod p= xα^ak(α^ka) ^-1mod p=xα⁰ mod p=x.

Проблема дешифрования заключается в вычислении сообщения по шифрограмме без использования секретного ключа.

Теорема

Проблема дешифрования для шифра ElGamal и проблема Диффи-Хеллмана вычислительно эквивалентны.

Доказательство:

Действительно, пусть A есть алгоритм решения проблемы Диффи-Хеллмана,

A(p, α, δ, γ)= 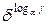mod p.

Тогда дешифрование для шифра ElGamal осуществляется следующим образом:

x=y₂A(p, α, y₁, β)^-1

(поскольку A(p, α, y₁, β)= A(p, α, α^k, α^a)= 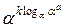mod p=α^ak mod p=β mod p).

Обратно, пусть B есть алгоритм дешифрования для шифра ElGamal, то есть

B(p, α, β, y₁, y₂)=x=y₂(y₁ 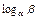)^-1 mod p.

Тогда проблема Диффи-Хеллмана решается следующим образом:

δ 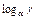=B(p, α, γ, δ, 1)^-1

□