Построение доказуемо простых чисел общего и специального вида.

7.1. Теорема Сэлфриджа и доказуемо простые числа общего вида на основании полного разложения (n—1).

Ранее мы изучили тесты на простоту, которые с некоторой малой вероятностью могут принять составное число за простое. Это – тесты Ферма, Соловея-Штрассена, Миллера-Рабина. Однако в некоторых случаях требуется построение доказуемо простых чисел, то есть чисел, простота которых доказана. Для этого существует класс тестов на простоту, которые могут принять простое число за составное, но не наоборот. Эти тесты основаны на теории групп.

Теорема Сэлфриджа.

Пусть n—1= 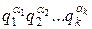. n – простое, 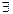a: 1) a^n—1≡1(mod n);

2) 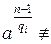1(mod n).

Доказательство:

Пусть n – простое число. Тогда (1) выполняется для всех a<n согласно теореме Ферма. В силу критерия Люка, найдется a: O_n(a)=n—1 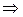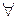s<n—1 выполняется a^s 1(mod n), а поскольку , < n—1, то выполняется (2).

Возьмем q₁. Пусть 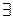a: 1) a^n—1≡1(mod n); 2) 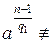1(mod n). Из (1) и (2) следует, что O_n(a)\(n—1) и O_n(a) не делит . Откуда из * следует, что 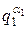\O_n(a). Согласно Теореме 3 (п.1), O_n(a)\φ(n)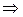 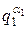\ φ(n).

Рассматривая аналогичным образом q₂, q₃,…,q_k, убеждаемся, что 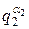\φ(n), 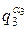\φ(n), … , \φ(n). Тогда 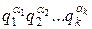=(n—1)\φ(n). Но последнее возможно только в случае, когда n—1=φ(n), то есть тогда, когда n – простое число.

□

Теорема Сэлфриджа дает удобный критерий для доказательства простоты числа. На основании этой теоремы построены алгоритмы проверки чисел на простоту, которые требуют полной или частичной факторизации числа n—1, а потому называются n—1 – методами.

В общем случае мы можем говорить о том, что число n—1 по крайней мере четное.

В том случае, когда нам известно полное разложение проверяемого числа на множители, можно использовать следующий

тест Миллера на простоту:

Вход: n – число для проверки, n—1= 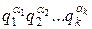- каноническое разложение, t – параметр надежности.

1. Выбрать t различных случайных чисел a_j: 1<a_j<n

2. Для каждого a_j вычислить a_j^n—1 mod n. Если какой-либо из результатов не равен «1», то идти на Выход с сообщением «n – составное число».

3. Для каждого q_i выполнить:

3.1. Для каждого a_j вычислить 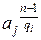mod n. Если какой-либо из результатов не равен единице, то идти на шаг 3, взять следующее q_i. Если все результаты равны «1», то идти на Выход с сообщением «вероятно, n – составное число».

4. Идти на Выход с сообщением «n – простое число».

Выход.

Замечание: Если t=n—2, то слово «вероятно» на шаге 3.1. следует убрать.

Если число n было предварительно проверено на простоту вероятностным тестом Миллера-Рабина, то в тесте Миллера достаточно перебрать 4-6 значений a_j.

Тест Миллера, основанный на теореме Сэлфриджа, пригоден для доказательства простоты любого нечетного числа, если известно разложение на простые сомножители числа, ему предстоящего. Однако этот тест достаточно трудоемок. Для некоторых чисел особого вида построены специальные доказательства простоты. Некоторые из таких чисел мы рассмотрим в п.3-4.

7.2. Теорема Поклингтона и доказуемо простые числа общего вида на основании частичного разложения (n—1).

Теорема Сэлфриджа дает четкий критерий для проверки простоты числа n, однако требует знания полного разложения числа (n—1) на простые сомножители. Следующая теорема позволяет ограничиться частичной факторизацией (n—1).

Теорема Поклингтона.

Пусть n=RF+1, F= 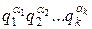- каноническое разложение.

Если 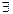a: 1) a^n—1≡1(mod n);

2) 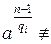1(mod n) .

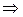p≡1(mod F) для любого простого p\n.

■

Итак, если разложить n—1 на два сомножителя n—1=RF, где F> 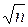—1, то, если для некоторого a будут выполнены условия Теоремы Поклингтона (1) и (2), то n – простое.

Таким образом, можно значительно сократить количество проверок по сравнению с тестом Миллера.

Замечание.

Если n=RF+1 – нечетное простое число, F> 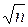—1, F= 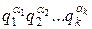, НОД(R,F)=1, то вероятность того, что случайно выбранное 1<a<n будет удовлетворять условиям (1), (2) теоремы Поклингтона, есть .

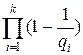Замечание.

Если известно полное разложение n—1, то в качестве F следует брать число, составленное из наибольших делителей n—1 для того, чтобы:

1) сократить число проверок условия (2) для каждого a;

2) уменьшить степени, в которые возводится a на этапе проверки (2);

3) повысить вероятность того, что случайно выбранное a будет удовлетворять условию (2), а значит уменьшить количество перебираемых a.

Пример.

n=4021. 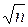—1<63.

n—1=4020=2²·3·5·67. F=67, R=2²·3·5=60.

Проверка условий:

a=2.

1) 2⁴⁰²⁰ mod 4021=1.

2)2⁶⁰—1 mod 4021=1451.

НОД(4021,1451)=1.

n=4021 – простое число.

(Заметим, что вероятность того, что наугад выбранное a будет удовлетворять условиям теоремы Поклингтона для данного примера, есть (1—1/67)≈0,985).