Непрерывность функции нескольких переменных
Пусть дана функция 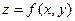 с областью определения
с областью определения 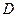 и пусть
и пусть 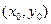 – предельная точка множества
– предельная точка множества 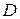 .
.
Определение. Говорят, что функция 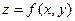 непрерывна в точке
непрерывна в точке 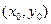 , если
, если
1) 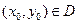 ;
;
2) 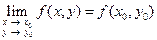 , т.е.
, т.е. 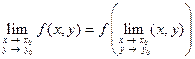 .
.
Сформулируем определение непрерывности в эквивалентной форме. С этой целью обозначим 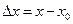 ,
, 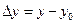 и
и 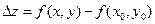 .
.
Определение. Говорят, что функция 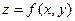 непрерывна в точке
непрерывна в точке 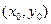 , если выполняется равенство
, если выполняется равенство
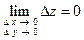 .
.
Теорема. Если функции 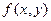 и
и 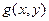 непрерывны в точке
непрерывны в точке 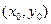 , то в этой точке непрерывны и функции
, то в этой точке непрерывны и функции 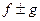 ,
, 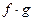 , а если
, а если 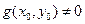 , то и функция
, то и функция 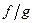 .
.
Определение.Функция 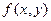 , определённая на некотором множестве
, определённая на некотором множестве 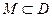 называется непрерывной на множестве
называется непрерывной на множестве 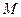 если она непрерывной в каждой точке множества
если она непрерывной в каждой точке множества 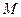 .
.
Определение. Множество 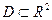 называется областью, если оно:
называется областью, если оно:
1) является открытым множеством, т.е. содержит каждую свою точку вместе с некоторой своей 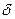 -окрестностью; 2) является линейно связным множеством, т.е. для любых двух различных точек
-окрестностью; 2) является линейно связным множеством, т.е. для любых двух различных точек 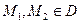 существует ломаная, соединяющая
существует ломаная, соединяющая 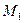 и
и 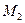 и целиком лежащая в
и целиком лежащая в 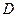 .
.
Если 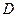 – область, то множество
– область, то множество 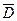 называют замкнутой областью.
называют замкнутой областью.
Определение. Говорят, что функция 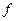 непрерывна в области
непрерывна в области 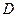 (или в замкнутой области
(или в замкнутой области 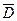 ), если
), если 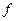 непрерывна в каждой точке этой области.
непрерывна в каждой точке этой области.
Дата добавления: 2015-11-28; просмотров: 482;
