Производные и дифференциалы функций
нескольких переменных
Определение. Пусть в некоторой области 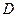 задана функция
задана функция 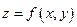 . Возьмем произвольную точку
. Возьмем произвольную точку 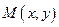 из этой области и дадим переменной х приращение
из этой области и дадим переменной х приращение 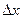 . Величина
. Величина 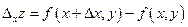 называется частным приращением функции по х.
называется частным приращением функции по х.
Рассмотрим отношение:
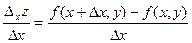 .
.
Если существует конечный предел 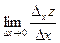 , то он называется частной производнойфункции
, то он называется частной производнойфункции 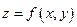 по х.
по х.
Обозначение: 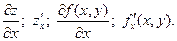
Аналогично определяется частная производная функции 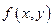 по у:
по у:
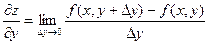 .
.
Геометрическим смысломчастной производной (например, 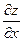 ) является тангенс угла наклона касательной, проведенной в точке
) является тангенс угла наклона касательной, проведенной в точке 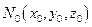 к сечению поверхности плоскостью
к сечению поверхности плоскостью 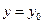 .
.
2. Полное приращение и полный дифференциал
Определение. Выражение 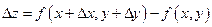 называется полным приращением функции
называется полным приращением функции 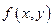 в точке
в точке 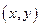 .
.
Если функция 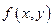 имеет непрерывные частные производные, то
имеет непрерывные частные производные, то
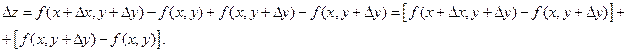 Применяя теорему Лагранжа к выражениям, стоящим в квадратных скобках, получим:
Применяя теорему Лагранжа к выражениям, стоящим в квадратных скобках, получим:
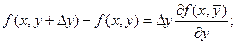
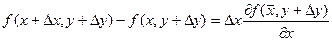 ,
,
где 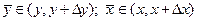 . Находим
. Находим
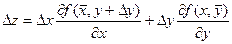 .
.
Так как частные производные непрерывны в точке 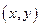 , то справедливы равенства:
, то справедливы равенства:
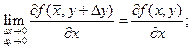
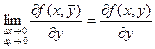 .
.
Определение.Выражение 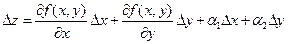 называется полным приращениемфункции
называется полным приращениемфункции 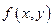 в точке
в точке 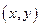 , где
, где 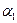 и
и 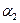 – бесконечно малые функции при
– бесконечно малые функции при 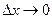 и
и 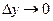 соответственно.
соответственно.
Определение. Полным дифференциаломфункции 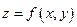 называется главная, линейная относительно
называется главная, линейная относительно 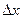 и
и 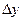 часть приращения функции
часть приращения функции 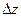 в точке
в точке 
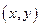 :
:
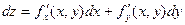
Для функции произвольного числа переменных имеем:
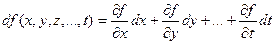 .
.
Пример. Найти полный дифференциал функции 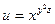 .
.
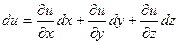 ;
; 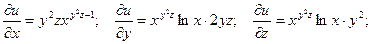
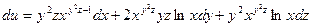 .
.
Пример. Найти полный дифференциал функции 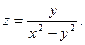
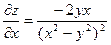 ;
; 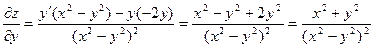 ;
;
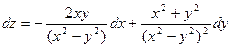 .
.
Дата добавления: 2015-11-28; просмотров: 563;
