Частные производные и дифференциалы высших порядков
Пусть функция 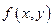 и её частные производные
и её частные производные 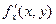 и
и 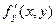 определена в некоторой области D. Если существуют частные производные функций
определена в некоторой области D. Если существуют частные производные функций 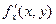 и
и 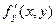 по
по 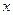 и
и 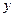 в этой области, то они называются частными производными второго порядка:
в этой области, то они называются частными производными второго порядка:
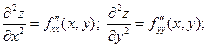
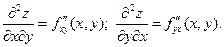
Аналогично определяются частные производные более высоких порядков от функции 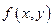 в области
в области 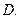
Определение. Частные производные по различным аргументам вида 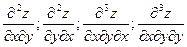
 и т.д. называются смешанными производными.
и т.д. называются смешанными производными.
Теорема. Пусть функция 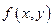 в некоторой окрестности
в некоторой окрестности 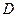 точки
точки 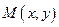 имеет частные производные
имеет частные производные 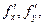 и смешанные частные производные второго порядка
и смешанные частные производные второго порядка 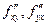 . Если
. Если 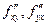 непрерывны в точке
непрерывны в точке 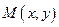 , то они совпадают в этой точке, т.е. в точке
, то они совпадают в этой точке, т.е. в точке 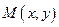 выполняется соотношение:
выполняется соотношение:
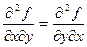 .
.
Пусть функция 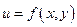 дифференцируема в некоторой окрестности точки
дифференцируема в некоторой окрестности точки 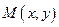 . Её дифференциал
. Её дифференциал
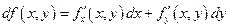
является функцией переменной точки 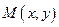 и функций приращений
и функций приращений 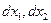 независимых переменных. Будем считать приращения независимых переменных постоянными , тогда дифференциал
независимых переменных. Будем считать приращения независимых переменных постоянными , тогда дифференциал 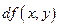 станет функцией точки
станет функцией точки 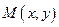 и от него, в свою очередь можно брать дифференциал, если этот дифференциал существует.
и от него, в свою очередь можно брать дифференциал, если этот дифференциал существует.
Определение.Дифференциалом второго порядка (вторым дифференциалом) функции 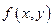 называется дифференциал от её первого дифференциала:
называется дифференциал от её первого дифференциала:
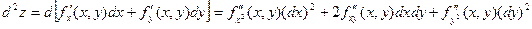 .
.
Аналогично определяются дифференциал третьего порядка от функции 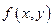 :
:
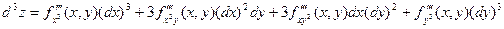
И вообще, дифференциал 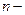 го порядка от функции
го порядка от функции 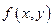 :
:
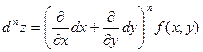 .
.
Здесь n – символическая степень производной, на которую заменяется реальная степень после возведения в нее стоящего в скобках выражения.
Дата добавления: 2015-11-28; просмотров: 560;
