Градиент. Связь градиента с производной по направлению

Определение. Если в некоторой области D задана функция 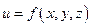и некоторый вектор, проекции которого на координатные оси равны значениям функции 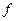в соответствующей точке

,

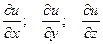то этот вектор называется градиентомфункции .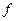

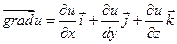
При этом говорят, что в области D задано поле градиентов.

Теорема: Пусть задана функция 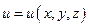и поле градиентов

.

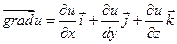Тогда производная 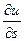по направлению некоторого вектора 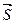равна проекции вектора 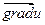на вектор .

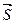Доказательство: Рассмотрим единичный вектор 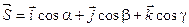и некоторую функцию 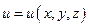и найдем скалярное произведение векторов 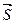и :

.

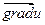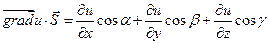Выражение, стоящее в правой части этого равенства является производной функции 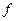по направлению 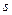, т.е.

.

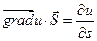Если угол между векторам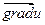и и 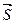обозначить через 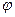, то скалярное произведение можно записать в виде произведения модулей этих векторов на косинус угла между ними. С учетом того, что вектор 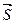единичный, т.е. его модуль равен единице, можно записать:

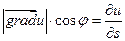
Выражение, стоящее в правой части этого равенства и является проекцией вектора 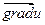на вектор 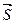. Теорема доказана.

Для иллюстрации геометрического и физического смысла заметим, что градиент – вектор, показывающий направление наискорейшего изменения некоторого скалярного поля 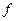в некоторой точке. В физике существуют такие понятия как градиент температуры, градиент давления и т.п., т.е. направление градиента есть направление наиболее быстрого роста функции.

С точки зрения геометрического представления градиент перпендикулярен поверхности уровня функции.