Непрерывность функции в точке
Определение. Функция 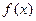 , определенная в некоторой окрестности точки
, определенная в некоторой окрестности точки 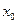 , называется непрерывной в точке
, называется непрерывной в точке 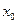 , если предел функции и ее значение в этой точке равны:
, если предел функции и ее значение в этой точке равны:
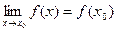
Тот же факт можно записать иначе: 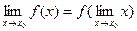 .
.
Определение. Если функция 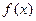 определена в некоторой окрестности точки
определена в некоторой окрестности точки 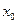 , но не является непрерывной в самой точке
, но не является непрерывной в самой точке 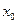 , то она называется разрывной функцией в этой, а сама точка
, то она называется разрывной функцией в этой, а сама точка 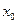 называется точкой разрыва этой функции.
называется точкой разрыва этой функции.
Пример непрерывной функции:
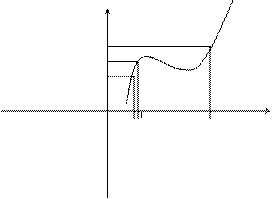 y
y
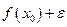
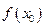
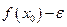
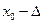
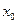
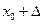 x
x
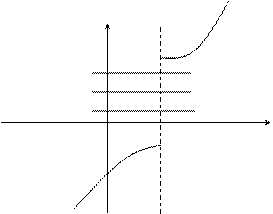
Пример разрывной функции:
 |
y
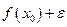
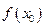
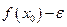
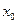 x
x
Определение. Функция 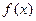 называется непрерывной в точке
называется непрерывной в точке 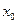 , если для любого положительного числа
, если для любого положительного числа 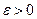 существует такое число
существует такое число 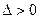 , что для любых
, что для любых 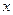 , удовлетворяющих условию
, удовлетворяющих условию
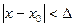 ,
,
выполняется неравенство
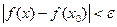 .
.
Определение. Функция 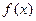 называется непрерывной в точке
называется непрерывной в точке 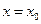 , если приращение функции в точке
, если приращение функции в точке 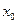 является величиной бесконечно малой в этой точке:
является величиной бесконечно малой в этой точке:
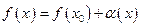
где 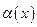 – функция бесконечно малая при
– функция бесконечно малая при 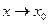 .
.
Если функция непрерывна в каждой точке множества 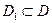 , то говорят, что она непрерывна на множестве
, то говорят, что она непрерывна на множестве 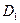 .
.
Непрерывная функция изображается на графике непрерывной кривой.
Дата добавления: 2015-11-28; просмотров: 1259;
